Bonjour

Je pose les équations suivantes :


D^2 =     441 + (X1-X2)^2+ (Y1-Y2)^2
D^2 =    729 + (X1-X3)^2+ (Y1-Y3)^2
D^2 =    900 + (X1-X4)^2+ (Y1-Y4)^2
D^2 =      36 + (X2-X3)^2+ (Y2-Y3)^2
D^2 =     81 + (X2-X4)^2+ (Y2-Y4)^2
D^2 =      36 +  (X3-X4)^2+ (Y3-Y4)^2

6 équations 5 Inconnues.

Résolution à venir.
@+

on peut supprimer une inconnue en prenant la position X1,Y1,Z1 comme origine du repère.

bonjour

autant pour moi , les altitudes sont : 30 , 51 , 54 & 60  .
j'avais écrit 57 au lieu de 54 . excusez moi .

Arf : j'avais trouvé que c'était possible, par exemple en plaçant les éperviers en (0;0;60) (0;33;57) (39V61/11;174/11;51) (3V61/11;153/11;30), pour une distance de 3V122.

Bon ben je vais recommencer avec les nouvelles valeurs

re ,

@Ebichu : je viens de recalculer avec la valeur 57 ; et c'est parfait !  bravo !

Sans calcul, on peut déjà avancer que ça marche quels que soient les écarts d'altitude.

Preuve : on place un tétraèdre régulier avec une arête verticale, et donc aussi une arête horizontale. L'altitude de l'arête horizontale est pile au milieu de l'arête verticale. En inclinant cette dernière selon le plan normal à l'arête horizontale, on peut placer l'altitude de cette dernière dans la proportion qu'on veut par rapport à la différence d'altitude entre les points extrêmes haut/bas du tétraèdre. Ensuite en faisant pivoter l'axe vertical incliné, on écarte l'altitude des 2 extrémités de l'axe horizontal, l'une vers le haut, l'autre vers le bas, de la même amplitude.

En application de ce qui vient d'être dit, on se rend compte que dans les données de l'énoncé, la moyenne des 2 altitudes intermédiaires est dans la proportion 1/4 - 3/4 de la différence des altitudes extrêmes. On en déduit après calcul l'inclinaison de l'axe vertical incliné, puis la distance entre sommets : 31,8198051533946
mètres.

@Ebichu : c'est exact pour la longueur ; je ne vérifie pas les coordonnées , je procède autrement sans calculer les coordonnées

@Nodgim : tu me donnes 13 décimales mais la première n'est pas bonne .

Je sais, je me suis planté complètement dans mon raisonnement.....

@Jackv : si oui il est demandé une réponse par le calcul ; pour l'instant que nenni .
Il n'y a qu'une valeur possible .

Je comprend maintenant pourquoi tu as modifié ton altitude de 57 à 54m. C'était pour rendre la résolution numérique de ton problème accessible à mes (faibles) compétences mathématiques !
Effectivement, l'altitude de mon point H, à mi-hauteur du point D par rapport au point A, simplifie les relations .

Si j'appelle D' la projection du point D sur le plan Z = 0, il suffit d'exprimer la distance AD' de deux manières différentes pour obtenir une équation en a (= distance entre chaque épervier).

Sans certitude sur l'exactitude de mes calculs, je te propose la valeur
                                           a = 31,8198051.

EDIT : Je n'ai pas utilisé la trigo, uniquement Pythagore Spoiler : [Afficher le message] (et un tableur )

Au départ, je suis parti d’un système d’équations sur les coordonnées des quatre points (en prenant x1 = y1 = 0):
D² = x2² + y2² + 441 = x3² + y3² + 576 = x4² + y4² + 900
et: D² = (x2-x3)² + (y2-y3)² + 9 = (x2-x4)² + (y2-y4)² + 81 = (x3-x4)² + (y3-y4)² + 36
En triturant les trois dernières équations, on arrive à:
½ D² = x2.x3 + y2.y3 + 504 = x2.x4 + y2.y4 + 630 = x3.x4 + y3.y4 + 720
A priori, avec six équations et six inconnues, c’est jouable, mais les calculs deviennent vite inextricables et j’abandonne donc cette piste.

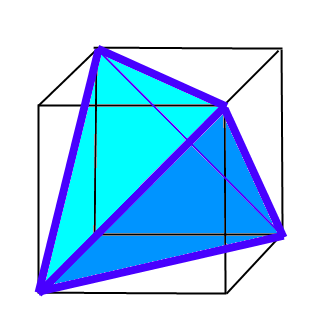
Puis je me suis aperçu que les quatre points définissent un tétraèdre régulier avec quatre faces en triangles équilatéraux. Ce tétraèdre est circonscrit dans un cube où les arêtes du tétraèdre (de longueur D) sont les diagonales du cube. Deux arêtes sans point commun sont ‘’perpendiculaires dans l’espace’’.
Pour les altitudes, je pars de: 0; 21; 24 et 30 (au lieu de: 30; 51; 54 et 60), ce qui ne change rien.
Je place le cube à plat et je l’incline d’un angle A suivant l’arête du tétraèdre au sol jusqu’à ce que le point opposé à celui d’altitude 0 ait une altitude de 21. L’altitude des deux autres points devient alors h0:
h0 = (D/2).[V(2/3).cosA + V(1/3).sinA]
J’incline maintenant ce cube (déjà incliné) d’un angle B perpendiculairement à l’arête 0-21 pour ramener les points supérieurs aux altitudes h1 = 60 et h2 = 24: on obtient (je ne détaille pas les calculs):
h1–h2 = 36 = D.sinB.cosA   /   h1+h2 = 84 = D.cosB.sinA + 21
d’où: D.cosA = (81/2).V2   avec: sinA = 21/D
et finalement: D = (3/2).V1654 = env. 61,004
Mais je ne suis pas vraiment sûr de ne pas m’être planté quelque part dans un calcul.

Bonjour unecoudée,

Si la réponse est de type a√b avec a et b entiers, j’ai peut être une erreur de calcul.

Pour (30 ; 51 ; 54 ; 60), je trouve une équidistance entre nos 4 amis avec une distance respective de  3√(227/2) m…
Avec les positions (x/y/z) approximatives suivantes : (0 / 0 / 30) ; (-10,82 / 21,53 / 51) ; (-18,98 / -9,23 / 54) ; (11,02 / 0 / 60). Ça a l’air de marcher pourtant…

Pour (30 ; 51 ; 57 ; 60) je trouve 3√122 m, avec comme positions : (0 / 0 / 30) ; (-5,76 / 24,98 / 51) ; (-18,55 / -5 / 57) et (14,07 / 0 / 60)

Bonne journée confinée.

bonjour à tous ,

Et merci de vous être intéressés à ce casse tête . Je vous donne ma façon de voir la chose en espérant être assez clair .

Résolution :

Déjà on peut changer l'échelle afin de simplifier les formules : 1/3  ; et on descend tout le monde de 10 m ; ainsi les distances entre les 4 niveaux sont :  0 , 7 , 8  & 10   . 
Les 4 objets forment donc un tétraèdre régulier . Maintenant on regarde le tétraèdre selon une direction parallèle aux 4 plans z=0 , z=7 .....
Un rappel : toute droite dans l'espace est contenue par un plan vertical .
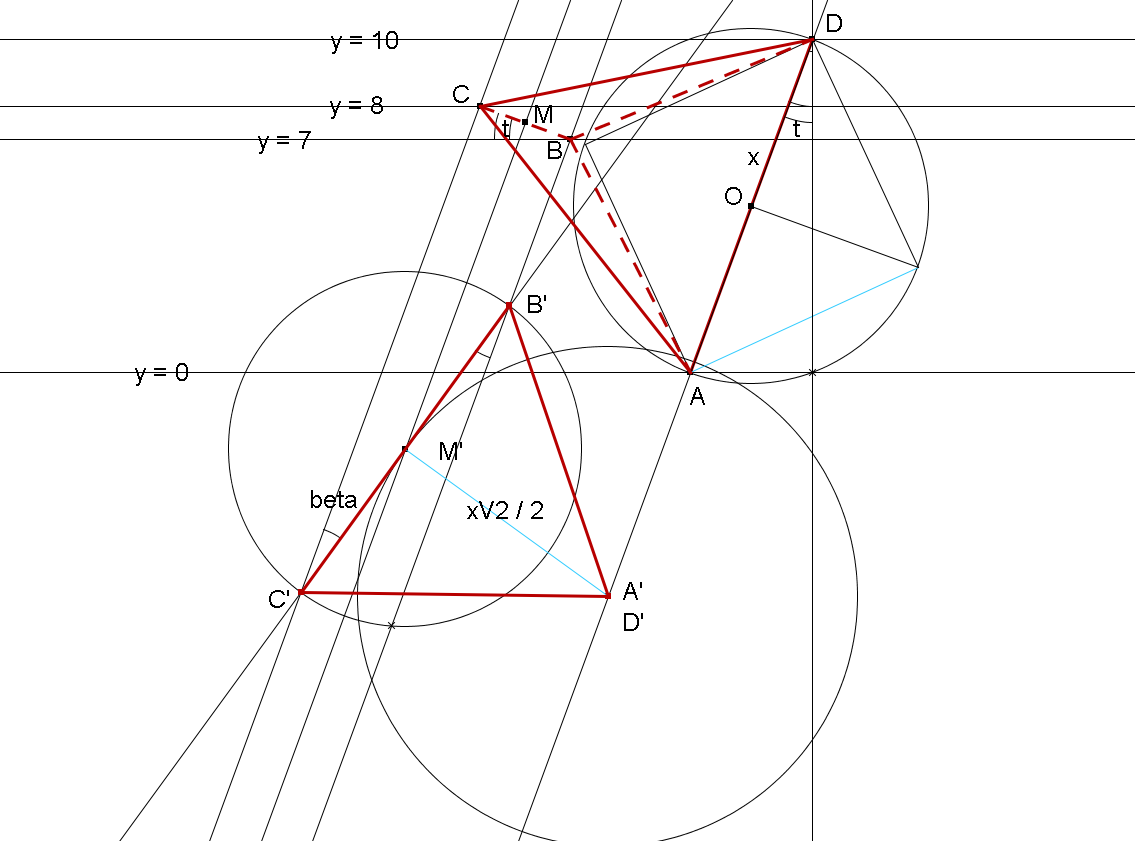
On peut tourner autour du tétraèdre afin de voir chacune de ses arêtes à tour de rôle  en vraie grandeur . On regarde par exemple l'arête AD .
A est le point le plus bas et D est le plus haut . AD vu en vraie grandeur forme avec la verticale un angle t  . 
Et les deux points B & C  se trouvent alors sur la médiatrice du segment AD , sur les droites d'équation : z = 7 & z = 8 .
Le segment BC quant à lui , forme un angle t avec l'horizontale .
Mais les 5 autres arêtes ne sont pas vues en vraie grandeur .
soit M le milieu du segment BC .
On trace les trois droites parallèles à AD passant par B , M & C .   
On trace maintenant le tétraèdre  A'B'C'D'  vu suivant DA ; ainsi que le point M' milieu de B'C'  .
On ne connaît pas l'angle t  . On suppose alors que c'est angle est connu et donc qu'il soit tracé correctement .

  L'angle B'C'C sera appelé :  [latex]\beta[/latex] .

Nous devons maintenant calculer ces deux angles pour connaître l'arête du tétraèdre .
Si la figure est correcte , alors : A'M'  est la distance entre les 2 arêtes opposées : B'C' & A'D' qu'on appellera x ( notre inconnue ) .
On connaît la valeur de cette distance entre deux arêtes opposée  :
[TeX]A'M' = \cfrac{\sqrt2}{2}.x[/TeX]
A partir du dessin , on peut formuler :
[TeX]x = \cfrac{1}{\sin{t}.\sin{\beta}}[/TeX]
Comme la distance  OC = A'M'  , et comme la différentielle d'ordonnées de O & C  est de 3 , alors :
[TeX]\cfrac{x.\sqrt2}{2}.\cos{\beta} + \cfrac{1}{2.\sin{t}}  = \cfrac{3}{\sin{t}}[/TeX]
On reporte dans cette dernière formule la valeur de  x , et après simplification et la disparition du  sin t  on trouve cette ligne trigo :
[TeX]\tan{\beta} = \cfrac{\sqrt2}{5}[/TeX]
On en déduit son sinus :
[TeX]\sin\beta = \cfrac{\sqrt6}{9}[/TeX]
Comme on sait aussi que :
[TeX]AD  =  x  = \cfrac{10}{\cos{t}}[/TeX]
Alors :
[TeX]\cfrac{10}{\cos{t}} = \cfrac{9}{\sqrt6.\sin{t}}[/TeX][TeX]\tan{t} = \cfrac{3.\sqrt6}{20}[/TeX]
Il reste à calculer le sin t  en fonction de sa tangente : 
[TeX]\sin{t} = 3.\sqrt\frac{3}{227}[/TeX]
On obtient enfin x :
[TeX]x = \cfrac{1}{\sin{t}.\sin{\beta}}[/TeX][TeX]x = \sqrt{\frac{227}{2}} \approx 10.6536..m[/TeX]
Mais comme au départ on a réduit l'échelle de 1/3 , la distance d séparant chacun des rapaces vaut :d = 31.961 m  arrondi au mm .

N.B.  Avec l'altitude 57 m : même processus mais les équations changent légèrement avec :
[TeX]x = \cfrac{2}{\sin{t}.\sin\beta}[/TeX]
et
[TeX]\cfrac{x.\sqrt2}{2}.\cos{\beta} + \cfrac{1}{\sin{t}}  = \cfrac{4}{\sin{t}}[/TeX]