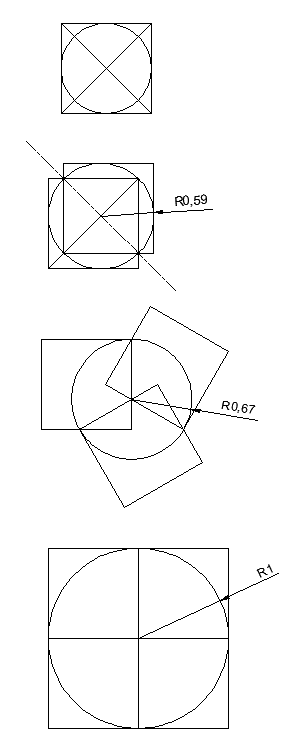
alors je reprends pour le 3 feuilles avec un joli dessin et tout et tout...
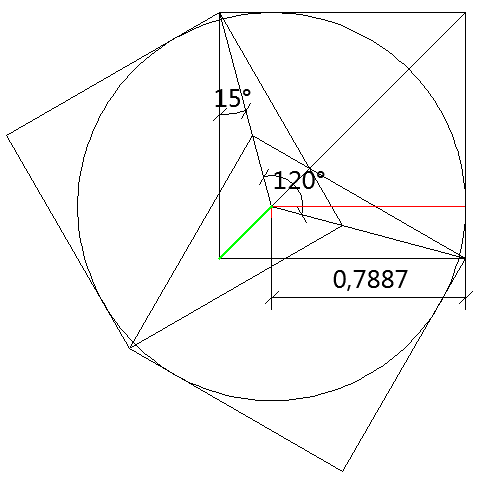
On voit bien sur cette forme que je peux encore disons tirer la feuille d'en bas a gauche un petit peu. Alors apparaitront aux points B,D,F des petits trous, jusqu'a toucher le cercle. Donc je garde cette forme sauf que je dis que le cote des feuilles est en fait ici 1+ε et je vais chercher a enlever le petit morceau qui va bien.
Plus precisement, la droite qui passe par B et G coupe le cercle en un point dont l'abscisse sera 1, ce qui determinera ε.
j'ai donc les coordonnes des points :
A=(0,0)
B=(1+ε,0)
C=((1+ε)(1+√32),1+ε2)
D=((1+ε)(1+√3)2,(1+ε)(1+√3)2)
E=(1+ε2,(1+ε)(1+√32))
F=(0,1+ε)
et celles du centre, en notant
ϕ=1+1/√32,
G=xA+xC+xE3(1,1)=(1+ε)1+1/√32(1,1)=ϕ(1+ε)(1,1)
Je cherche l'intersection H avec
xH=1 entre le cercle et (BG) :
D'abord H est sur BG, donc
BG×BH=0
soit
0=(1+ε)(ϕ−1ϕ)×(−εyH)
donc
(ϕ−1)y+εϕ=0
Et puis H est sur le cercle de centre G de rayon
r=(1+ε)ϕ donc
r2=GH2=(1+ε)2ϕ2
soit
(1−r)2+(y−r)2=r2
la premiere equation donne aussi
(ϕ−1)y+εϕ+ϕ=ϕ
soit
(ϕ−1)y+r=ϕ
en multipliant l'equation du cercle par
(ϕ−1)2, on a
(ϕ−1)2(1−r)2+(y(ϕ−1)⏟=ϕ−r−r(ϕ−1))2=r2(ϕ−1)2
et on a plus qu'a trouver r en fonction de
ϕ , ce qui donne
(ϕ−1)2(1−r)2+ϕ2(1−r)2=r2(ϕ−1)2
soit
((ϕ−1)2+ϕ2)(1−r)2=r2(ϕ−1)2
d'ou l'elimination du membre de droite
((ϕ−1)2+ϕ2)(r2−2r+1)=r2(ϕ−1)2
ϕ2r2−2((ϕ−1)2+ϕ2)r+((ϕ−1)2+ϕ2)=0
et on resoud
Δ=4((ϕ−1)2+ϕ2)2−4ϕ2((ϕ−1)2+ϕ2)=4((ϕ−1)2+ϕ2)(ϕ−1)2
et
r=2((ϕ−1)2+ϕ2)±2(ϕ−1)√(ϕ−1)2+ϕ22ϕ2=((ϕ−1)2+ϕ2)±(ϕ−1)√(ϕ−1)2+ϕ2ϕ2...
y a peut etre plus simple... et je sais toujours pas si j'ai bon...
Accueil
J'éditerai donc si j'avance.
McFlambi, et ton résultat pour deux feuilles.
