 |
#26 - 29-05-2020 14:02:27
- caduk
- Professionnel de Prise2Tete
- Enigmes résolues : 45
- Messages : 398
Echecs 2
Configurations aboutissant à une impossibilité (Je démontre en plus toute l'étendue de mes compétences en arts ascii  ) : ) :
Premier cas de figure : deux quasi boucles reliées (elles peuvent bien évidemment être dans l'autre sens, et être plus grandes, et avec des virages)
Deuxième cas de figure : Une quasi boucle reliée à une boucle fermée sauf en 1 point. Pareil, les deux boucles peuvent être plus grandes, il faut par contre que la quasi boucle se resserre pour que le deuxième mouvement forme toujours une boucle fermée.
Je ne sais pas encore si il y a d'autre configurations. Je pense que l'on peut ramener tout les cas impossibles à ce genre de configurations, et dans le cas contraire, on peut détruire toutes les quasi boucles et procéder à ma méthode pour vider la grille.
#27 - 29-05-2020 19:21:21
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Ehcecs 24
Ca reste tout de même très compliqué , il resterait à voir si ça généralise beaucoup le problème initial . La solution du problème impose simplement que chaque robot sur une ligne paire pointant vers le nord ou le sud ait une case de libre devant lui . On peut remplacer pair par impair ou ligne par colonne ce qui laisse pas mal de possibilités . Est-ce que tu vois des positions types pour lesquelles ta méthode apporte une solution qui ne serait pas fournie par l'autre méthode ? A part bien sûr de libérer de façon évidentes certaines cases avant la première étape .
Et comment caractériser simplement les grilles pouvant être vidées ( j'ai des craintes ) .
Vasimolo
#28 - 29-05-2020 19:36:54
- caduk
- Professionnel de Prise2Tete
- Enigmes résolues : 45
- Messages : 398
ecgecs 24
Ca apporte beaucoup plus de possibilités, car pour être bloqué dans ma méthode, il faut avoir de base des quasi boucles, ou des boucles complètes mises à part un robot, ce qui est très exigeant (il faut qu'il y ait une grande densité de robots) De plus, si ces quasi boucles et boucles quasiment fermées sont suffisamment séparées les unes des autres de manière à ce qu'elle soient indépendantes, on peut les "désamorcées" facilement et se ramener à ma méthode. Les seuls cas où ma méthode ne marche pas sont les cas où pour en désamorçant une quasi boucle, on en amorce une nouvelle, voire on complète une boucle... comme dans les deux exemples que j'ai données ci dessus. On voit que c'est d'ailleurs dans ces cas de figure que l'on a des configurations impossibles non triviales...
Je pense qu'il est possible de lister toutes les configurations impossibles non triviales, et dans les autres cas, de trouver une méthode permettant d'éliminer toutes les quasi boucles et boucles quasiment fermées...
#29 - 31-05-2020 12:39:58
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
rchecs 24
Une solution en couleur :
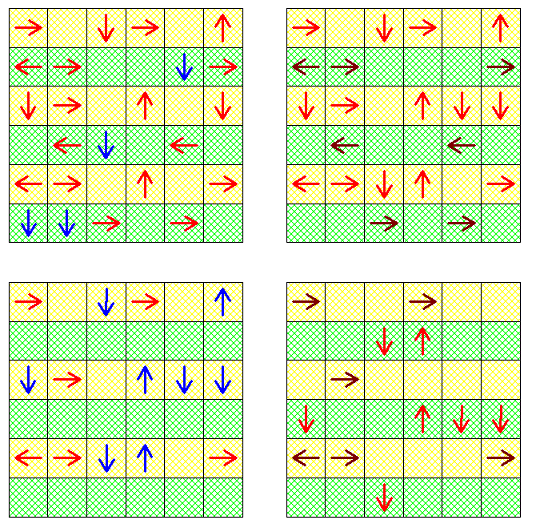
Les bleus se déplacent d'une case et les marrons sortent du jeu .
Merci aux participants 
Il reste la proposition de Caduc .
Vasimolo
#30 - 01-06-2020 12:36:23
- caduk
- Professionnel de Prise2Tete
- Enigmes résolues : 45
- Messages : 398
rchecs 24
Bon, voici la solution dans le cas général, en fait, ce n'était pas si dur.
En fait il s'agit de prendre le problème à l'envers. Il s'agit de trouver la solution d'un jeu à un joueur. Il faut le prendre à l'envers, en partant des positions perdantes où l'on est complètement coincées et en cherchant récursivement toutes les positions qui ne peuvent mener qu'à une solutions perdante.
La démo est un peu longue, mais elle est assez simple (c'est juste que je la détaille bien rigoureusement)
Une propriété remarquable (et relativement évidente) : Si on rajoute des robots à une solution perdante (dans les cases vides), elle reste perdante.
On définit récursivement une structure de base comme suit :
Un cycle de robots est une structure de base (les robots se touchent)
Pour tout angle d'un structure, on retire le robot situé à l'ange et on rajoute un autre cycle de robots au niveau des extrémités libres, tels que les directions des nouveaux robots soient les même que celle du premier cycle.
Exemple de transformation :
Bien entendu, la boucle ajoutée ne doit pas chevaucher la structure préalablement construite. La récurrence n'est possible que si on peut ajouter un cycle au niveau du coin enlevé.
Les structure des bases forment donc une arborescence de cycles reliés entre eux (avec une case vide au niveau des intersections).
On montre facilement par récurrence que les structures de base sont des positions perdantes, puisque tout les mouvements possibles sur une structure de base font apparaître une nouvelle structure de base, et contenant moins de cycles.
On définit les structures généralisée par récursion par récursion :
Les structures de bases sont des structures généralisées.
On définit une intersection comme une case vide où deux robots pointent dessus (éventuellement de loin), et une scission comme une case vide où un seul robot pointe dessus. (ces définitions sont valables seulement pour les structures généralisées, pas pour les positions de robots de manières générales)
Prenons une intersection ou une scission. Si un robot s'éloigne de cette case vide, alors on peut le faire reculer. La structure ainsi obtenue est aussi une structure généralisée.
A nouveau, quelques exemples.
De même, il est très facile de montrer que les structures généralisées sont perdantes, puisque tout mouvement possible créé une nouvelle structure généralisée. (et comme il ne peut y avoir de cycle, on finit par tomber sur une position ou tout mouvement est impossible)
On peut enfin compléter notre famille en disant que toutes les positions contenant au moins une structure généralisée sont perdantes (grâce à notre propriété remarquable)
Théorème : Les solutions perdantes ainsi construites sont les seules positions perdantes de ce jeu.
Soit une position telle que tout mouvement crée une position contenant au moins une structure généralisée. On va montrer que cette position contient alors une structure généralisée.
Effectuons un de ces mouvements et considérons une structure généralisée de la nouvelle position. On va effectuer tout les mouvements inverses possibles et montrer que l'on a toujours une structure généralisée. On a deux cas de figure pour les mouvements. Soit le robot reculé appartient à la structure généralisée considérée, soit pas. Dans le deuxième cas, comme on ne touche pas à la structure généralisée, c'est évident.
Etudions le premier : Les seules robots que l'on peut reculer sont soient au niveau d'une intersection ou d'un scission, soit au niveau d'un angle de l'un des cycles. Dans le premier cas, par construction, on sait que l'on obtient une structure généralisée.
Le deuxième cas est le plus délicat.
En faisant reculer un robot d'un coin d'un cycle, la case libérée par ce robot fait apparaître deux mouvements possibles :
- faire avancer le robot que l'on a reculé (ce qui recrée évidemment la structure généralisée que l'on avait)
- faire avancer le robot qui pointait initialement vers ce robot dans le cycle.
Dans ce cas, soit il existait une autre structure généralisée, auxquelles cas elle existera toujours, soit il faut s'arranger pour que ce déplacement crée une structure généralisée (car on a supposé qu'après tout déplacement, il existe une structure généralisée).
Faisons donc avancer ce robot et construisons une structure généralisée contenant ce robot. Les chemins extérieurs d'une structure généralisée aboutissant toujours à des intersections ou scissions de la structure généralisée, la structure ainsi ajoutée ne peut intersecter la précédente (excepté au niveau du robot avancé. Aussi, le robot avancé appartient forcément à un coin d'un cycle de la nouvelle structure généralisée. En faisant reculer ce robot, les deux structures généralisées se combinent en une plus grande structure généralisée. (Par le même principe que quand on ajoutait des cycles sur les structures de base).
La position initiale comportait donc une structure généralisée.
Pour résumer, les positions perdantes sont les positions contenant une structure généralisée. La stratégie pour vider les robots (à partir d'une position gagnante) est de n'effectuer que des mouvements conduisant à des positions gagnantes. Il existera toujours un tel mouvement car dans le cas contraire, à cause de notre théorème, notre position devrait être perdante.
#31 - 02-06-2020 09:41:55
- godisdead
- Expert de Prise2Tete
- Enigmes résolues : 22
- Messages : 747
Echesc 24
En lisant les réponses de chacun, il me vient une idée.
Si on réfléchit en terme de damier.
Etape 1 : on avance tous les robots de cases blanches (les cases noirs devant sont forcément vide)
Etape 2 : on avance tous les robots de cases noires (on vient de libérer les cases blanche)
Etc.
Je laisse, mais ça ne fonctionne pas ... 
#32 - 02-06-2020 15:06:31
- Migou
- Expert de Prise2Tete
- Enigmes résolues : 17
- Messages : 646
- Lieu: Ville 2/N près 2*i
ecgecs 24
Salut godisdead, attention aux collisions. Deux robots peuvent convoiter la même case cible.
|_|_|
|_|v|
|>|_|
#33 - 02-06-2020 18:50:45
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Echecss 24
@Caduk .
J'ai commencé à regarder ta solution "simple" , c'est vraiment trop compliqué . Oublie un moment la démonstration , comment va tu repérer simplement si une grille est gagnante ou pas .
Après je regarde le détail avec une boîte d'aspirine 
Vasimolo
#34 - 04-06-2020 15:30:11
- caduk
- Professionnel de Prise2Tete
- Enigmes résolues : 45
- Messages : 398
checs 24
Ma démonstration n'est effectivement pas très constructive, et c'est dur d'en extraire un algorithme efficace. Si l'on applique naïvement la démo, la méthode pour reconnaître une position perdante ressemblerait à ça :
prendre tout les les sous-ensembles de robots (Il y en a un nombre exponentiel  ) et regarder s'ils forment une structure généralisée. ) et regarder s'ils forment une structure généralisée.
La question est de savoir reconnaître une structure généralisée.
Pour reconnaître une structure de base, c'est assez simple (et polynomial pour une position donnée, ça s'applique même sur une position quelconque sans avoir à considérer tout les sous ensembles)
- tracer le graphe des robots (on relie chaque robot au robot qu'il pointe). Les structures de bases potentielles sont les cycles de ce graphe. (Sauf si une intersection de l'une des structures de base est obstruée, mais dans ce cas, ça forme une structure de base plus petite, donc on ne loupera pas l'existence d'une structure de base)
Pour chacun de ces cycles :
- Tracer ce chemin (en traçant un trait qui passe successivement par tout les robots du chemin). Le dessin obtenu doit être une arborescence de cycles reliés entre eux, et il doit y avoir des robots sur tout le chemin, excepté aux intersections.
Pour reconnaître les structures généralisées, j'avais une idée (qui ne marchait que si la position est une structure généralisée stricte, donc sans autres robots présent, ce qui implique de tester chaque sous ensemble de robots)
Le principe est de faire avancer les robots devant une scission, ce qui nous ramène à une structure de base, puis on fait comme au dessus.
Cependant, je me suis aperçu que je suis peut-être allé un peu trop vite dans ma démo. En effet, cette position là (perdante) n'est pas clairement décrite dans ma démo :
Ici, on a donc fait reculer l'un des robots à travers deux intersections (là où ma démo ne fait reculer qu'à travers une.
La question est : est ce que la case devant ce robot est une scission ou une intersection. En effet, quand on fait reculer un robot depuis une structure de base, il laisse devant lui une scission, or la case immédiatement devant lui est pointée par un autre robot, ce qui, selon la définition que j'avais donnée, est une intersection. Ce contre exemple ne modifie pas outre mesure ma démo, mis à part que j'ai des difficultés à définir proprement ce qu'est une scission. Ca demanderait clarification dans la démo.
Un autre point un peu trouble dans ma démo est le passage ou je fait reculer un robot situé à un angle et que je me débrouille pour que chaque mouvement possible crée bien une une structure généralisée. On voit sur cette nouvelle position que le robot le plus haut à gauche est un coin, mais qu'il ne rentre pas tout à fait dans le cadre de ma démo. Bien que je n'ai pas trouvé de nouvelle configuration à partir de là, il faudrait rendre cette partie de la démo plus rigoureuse.
Quand à trouver un algo efficace pour reconnaître les questions gagnantes ou perdantes, ça demeure une bonne question 
Je m'aperçois que ma démo n'est en fait pas si simple 
|
 |

 Accueil
Accueil
 Forum
Forum







