Je ne parviens pas à "uniformiser" parfaitement
Le mieux que j'ai trouvé est "2 cases restantes", en 30 changements : 

Je me doute que cela ne marche pas (??) car avec un cache de 3x2, les dimensions utilisées n'ont pas même parité (3 est impair, et 2 pair).

Enfin ce n'est qu'un idée, je ne suis qu'une bête, haha

Soit N le nombre de cases initialement noires.

Le cache va transformer k cases noires en cases blanches, et 6-k cases blanches en cases noires. On aura donc, après cette transformation, N+6-2k cases noires.

Le nombre de cases noires gardera donc sa parité quoi qu'il arrive. Si le nombre de cases noires est initialement impair, impossible de les rendre toutes noires (ou toutes blanches, de la même façon).

La flemme de m'attaquer au cas pair. Demain, peut-être ?

Après la grille 8x8, je me suis essayé à une grille 7x7, avec toujours avec le même "cache" de 3x2 :
- en 22 mouvements, je suis arrivé à blanchir toutes les cases, sauf UNE : la case centrale (4;4)
- en 20 mouvements, idem sauf UNE, dans le coin supérieur droit

Non, mais sur ton conseil, ça le fait bien
En 32 coups, tout l'échiquier 7x7 est noirci :




Edit: Et voici une autre solution du 7*7, un peu plus courte :

@Nodgim

Ta formule est juste mais : "avec un 8*8, pas de solution possible , problème de symétrie" est argument un peu expéditif Tu peux détailler ?

Vasimolo

Bonjour,

Avec tes deux indices, la solution devient accessible pour moi.

On remarque tout d'abord que, quel que soit l'endroit où l'on place le cache 3x2 sur la grille, celui-ci recouvre exactement deux points rouges, pas plus et pas moins. Si les deux points rouges sont sur deux cases blanches, ils deviennent après changement de couleur sur deux cases noires. Et vice-versa. Et si les deux points rouges sont sur deux cases de couleur différente, ils restent après changement de couleur sur deux cases de couleur différente.

Autrement dit, la parité du nombre de points rouges sur case noire est un invariant, ainsi que la parité du nombre de points rouges sur case blanche.

Comme il y a 11 points rouges sur case noire, il ne peut jamais y avoir zéro point rouge sur case noire, donc il y aura toujours au moins une case noire.
=> la grille 8x8 ne peut pas être blanchie.

Si l'on pivote cette grille 8x8 d'un quart de tour, on remarque que les positions blanche et noire sont inversées. Le même raisonnement permet alors de conclure que la grille 8x8 ne peut pas être noircie.

CQFD.

J'attends maintenant la question suivante, qui sera "à quelle condition sur la taille de la grille celle-ci peut-elle être blanchie ou noircie ?"
Merci pour ce problème.
Klim.

Merci pour la participation , je vous laisse lire la réponse de Klim qui est très proche de celle j'aurais pu proposer .

Pour la généralisation , il est clair que la même stratégie montre qu'aucun carré de côté pair ne peut être uniformiser . Il semble ( sans preuve ) que tout carré impair peut être colorié uniformément . Je n'ai pas réfléchi au cas général d'un rectangle mXn , avis aux amateurs

Vasimolo

Vasimolo a écrit:

Pour la généralisation , il est clair que la même stratégie montre qu'aucun carré de côté pair ne peut être uniformisé.

C'était mon premier réflexe, mais j'ai préféré ne pas l'écrire.
En effet, c'est loin d'être évident pour un carré 6x6.

Quelqu'un y a-t-il réfléchi ?

Klim.

Bonjour,

En attendant que quelqu'un se colle à la généralisation, voici comment blanchir une grille 6x6. Utilisez le zoom pour mieux voir les grilles.



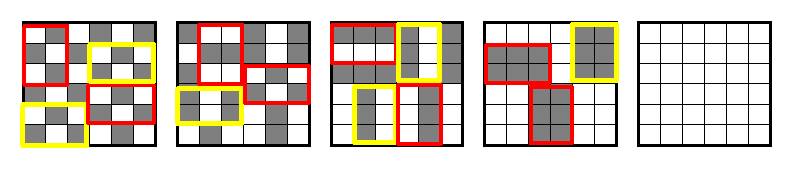
Il va de soi que le même procédé permet de noircir la grille (il suffit de tout permuter d'un quart de tour).

klim.