 |
#1 - 01-06-2012 20:16:58
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
#2 - 01-06-2012 20:33:09
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
Echecs 122
Tu ne dis pas où sont les blancs au départ du jeu ?
#3 - 01-06-2012 23:10:27
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Echcs 12
Une partie de la question est justement de savoir comment disposer les pièces pour pouvoir en éliminer un maximum 
Vasimolo
#4 - 01-06-2012 23:36:31
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3230
- Lieu: Luxembourg
Ecehcs 12
Bonjour à tous,
J'en suis à 4 pièces (2 pions blancs et 2 pions noirs):
N N N N
N B N B
N B N B
N B N B
N B N B
N B N B
N B N B
B B B B
B mange 7N en montant, puis N mange 7B en descendant,
et tout cela une deuxième fois.
Bonne soirée.
Edit: Je suis un âne: j'ai mal lu l'énoncé: on a 64 pions (pas 32):
je reviendrai plus tard sur cette énigme
#5 - 01-06-2012 23:39:03
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Echec 12
Attention Franky toutes les cases sont occupées ( les noires et les blanches ) !
Vasimolo
#6 - 02-06-2012 00:08:29
- alorc63
- Passionné de Prise2Tete
- Enigmes résolues : 47
- Messages : 55
- Lieu: En pleine cambrousse
Ehecs 12
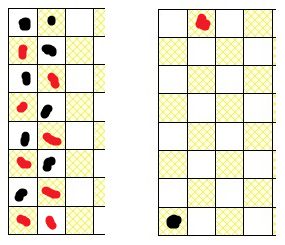
Salut!  est-ce que cette solution est acceptable? est-ce que cette solution est acceptable?
Il resterait 4 pions blancs en haut à droite et 4 pions noirs en bas à droite.
#7 - 02-06-2012 03:18:04
- jeje76360
- Amateur de Prise2Tete
- Enigmes résolues : 0
- Messages : 2
#8 - 02-06-2012 06:54:18
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,039E+3
cEhecs 12
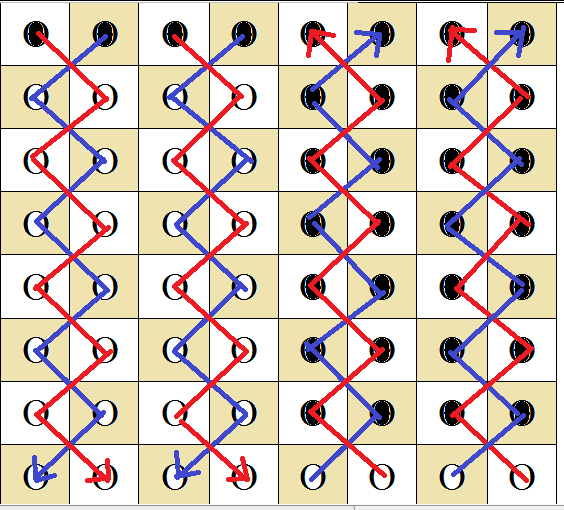
J'ai séparé les deux réseaux qui s'excluent pour plus de clarté.
Il en reste 2 et on peut très bien alterner un coup noir avec un coup blanc avançant d'une seule case à chaque fois , il suffit de changer de réseau à chaque fois...
#9 - 02-06-2012 08:47:08
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
Echesc 12
Dans ces conditions, c'est vraiment trop facile: les blancs peuvent prendre tous les noirs sans prendre un seul pion.
#10 - 02-06-2012 09:57:21
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
exhecs 12
Un petit bilan .
alorc : Spoiler : [Afficher le message] c'est bon mais on peut faire mieux .
jeje : Spoiler : [Afficher le message] je demande à voir 
gwen : Spoiler : [Afficher le message] parfait et superbement illustré 
nodgim : Spoiler : [Afficher le message] le but n'est pas de manger les noirs en préservant les blancs mais de laisser un minimum de pièces sur le plateau ( toutes couleurs confondues ) .
Vasimolo
#11 - 02-06-2012 10:57:12
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
Ehecs 12
Curieusement, c'est à peu près le même problème....
Placement des blancs (qui montent): toute la ligne du bas et depuis le bas, 2 colonnes de 2 rangs qui montent jusqu'à la ligne du haut exclue. Donc montage symétrique pour les noirs.
On joue seulement les pions extrémité des colonnes adverses, soit 4 pions noirs en haut et 4 pions blancs en bas. Chacun de ces pions ramasse la moitié d'une colonne. Au final , il ne reste que 4 blancs et 4 noirs.
#12 - 02-06-2012 17:59:28
- pierreM
- Habitué de Prise2Tete
- Enigmes résolues : 17
- Messages : 49
Echeecs 12
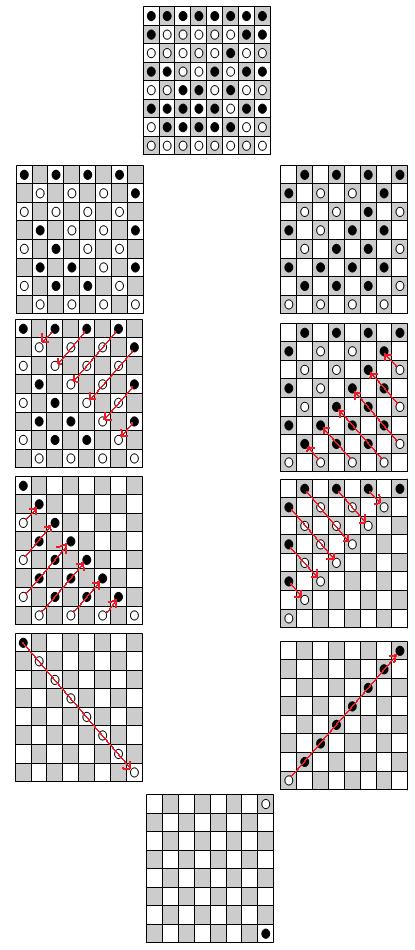
On aura au final 8 pions, avec une disposition contenant 4 colonnes comme celle-ci:
(début ==> fin)
Pour démontrer qu'on ne peut pas faire mieux: un pion ne peut manger que 7 pions au max. Du coup il doit rester au moins n/8 = 8 pions.
édité: j'avais lu 32 pions au total, pas 32 de chaque
édité2: la "démonstration" ne montre rien du tout... C'est plutôt de l'autopersuasion.
#13 - 02-06-2012 18:25:56
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Ehcecs 12
Une seule bonne réponse 
J'ai ajouté un petit indice et un peu de temps 
Vasimolo
#14 - 02-06-2012 20:24:41
- elpafio
- Elite de Prise2Tete
- Enigmes résolues : 43
- Messages : 1017
#15 - 03-06-2012 09:56:59
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
Echhecs 12
Après réflexion, j'arrive à ne laisser que 6 pions, l'africain.
#16 - 03-06-2012 11:30:45
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
ecgecs 12
J'ai ajouté un deuxième indice 
Vasimolo
#17 - 03-06-2012 11:37:25
- shadock
- Elite de Prise2Tete
- Enigmes résolues : 39
- Messages : 3334
Echecs 21
Juste les pions sont disposés de manière aléatoire ?
Sinon je vais faire mon dessin, je pense que 5 est le minimum.
Shadock
"L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
#18 - 03-06-2012 11:41:56
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Echeccs 12
Non Shadock , tu choisis la position pour tâcher d'éliminer le maximum de pièces .
Vasimolo
#19 - 03-06-2012 12:06:17
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
echevs 12
Vu, pourquoi n'ai je pas pensé à ça ?
On pose les pions comme aux dames, chaque couleur dans son camp, sauf que bien entendu on emplit à la fois les cases noires et les cases blanches. En s'y prenant bien, on arrive à ne laisser qu'un seul pion par couleur de case, c'est à dire 2 pions à la fin.
Je suis impardonnable, car je connais très bien le jeu de dames..
#20 - 03-06-2012 13:36:04
- dhrm77
- L'exilé
- Enigmes résolues : 49
- Messages : 3004
- Lieu: Fanning Island-?-Lac Tele,Mali
Echecs 2
Considerant que l'on a 2 jeux independants, Il parait evident que l'on puisse laisser 2 pions seulement a la fin. Ceppendant, si l'on inclu le deplacement vertical tout droit d'un pion normal qui ne mange pas, on doit pouvoir arriver a un pion unique qui reste.
Great minds discuss ideas; Average minds discuss events; Small minds discuss people. -Eleanor Roosevelt
#21 - 03-06-2012 13:40:33
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
#22 - 03-06-2012 17:19:08
- pierreM
- Habitué de Prise2Tete
- Enigmes résolues : 17
- Messages : 49
Echecs 112
Ah j'ai trouvé:

- les blancs remontent jusqu’à la diagonale
- les noirs redescendent de même
- le blanc en bas à gauche remonte la diagonale, il n'en reste qu'un.
Pour les cases jaunes, symétrie
==>il en reste 2, et là c'est évident qu'on peut pas faire mieux.
#23 - 03-06-2012 18:08:24
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Echecs 112
Bravo Pierre !
Vasimolo
PS : Nodgim : Spoiler : [Afficher le message] je crains que ta solution ne tienne pas la route !
#24 - 07-06-2012 22:57:05
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,039E+3
Echecs 1
Je m'interroge toujours sur l'unicité de la solution. A part changer la couleur des 6 cases centrales de chaque diagonale, je ne trouve rien d'autre.
#25 - 08-06-2012 19:17:02
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Echecs 112
Une panne d'ordinateur m'a laissé sans voix pendant quelques jours 
Merci à tous les participants en général et à Gwen en particulier , je vous renvoie à sa solution .
Vasimolo
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum












