 |
#1 - 03-06-2020 07:28:38
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
Beeghin Say
Un curieux problème vu sur un site voisin et pour lequel je n'ai pas de réponse définitive....
Tous les matins, je mets un 1/2 sucre dans mon café. Le dernier morceau du paquet est toujours un demi-morceau, mais celui de la veille ?
On supposera l'équiprobabilité de pioche entre un 1/2 morceau et un morceau entier.
#2 - 03-06-2020 08:03:29
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
beggin say
Il faut supposer qu'on pioche dans une boîte contenant initialement N morceaux tous complets et que la moitié inutilisée est remise dans la boîte ?
Vasimolo
#3 - 03-06-2020 11:12:17
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
Begihn Say
Il faut supposer qu'on pioche dans une boîte contenant initialement N morceaux tous complets et que la moitié inutilisée est remise dans la boîte ?
Vasimolo
Je copie ta question, la réponse est oui.
La question porte surtout sur une boîte contenant beaucoup beaucoup de morceaux...
#4 - 03-06-2020 13:01:59
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,043E+3
beghin day
En théorie, elle est de 1/N 
Si on considère le moment inévitable ou il reste un seul morceau de sucre intact, et qu'on évacue le cas "premier tirage" parfaitement équilibré, chaque morceau a une chance sur N d'être tiré en dernier, y compris le morceau de sucre intact.
#5 - 03-06-2020 16:10:38
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
Begihn Say
@ Gwen: tu ne dis pas ce que ça représente, ce 1/N. Je crains que ce ne soit un peu plus compliqué.
#6 - 03-06-2020 16:17:40
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,043E+3
Beghn Say
N est le nombre de sucres, et, au contraire, je pense que c'est bien plus simple qu'il n'y paraît.
#7 - 03-06-2020 17:47:04
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
beggin say
@ Gwen : c'est possible, mais il faut étayer un peu plus ton idée.
La question réelle est de connaitre la probabilité qu'il reste 2 demi-sucres au lieu de 1 sucre entier dans le paquet.
#8 - 03-06-2020 18:30:39
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,043E+3
BBeghin Say
En fait, non, ça ne marche pas mon truc.
A l'instant "t" il y a de fortes chances que certains sucres soient déjà entièrement mangés, ce qui augmente considérablement les chances.
#9 - 09-06-2020 15:31:57
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
Beghin Sayy
Salut !
Bon j'ai testé avec 4 situations basiques de départ. Je trouve qu'avec :
*Un sucre entier au début on a 0% de chance que celui de la veille soit un demi morceau
*2 sucres entiers au départ on a 50% de chance que l'avant dernier soit un demi morceau
*3 sucres entiers on a 11/18 chances
*4 sucres entiers on a 191/288 chances.
J'espère ne pas avoir fait d'erreurs de calcul, si vous les voulez je peux les joindre.
Avec un grand nombre de morceaux, ça donne :
On commence avec n demi sucres et p sucres entiers. On a n chances sur n+p de prendre un demi sucre et p chances sur n+p d'en prendre un entier. voir les calculs ci-dessous pour connaître le nombre de sucre restant dans chaque cas.
En supposant que la proportion se stabilise à partir d'un nombre assez grand de répétition, alors le rapport n/p ne devrait pas changer.
En égalant cette proportion avant piochage d'un sucre à celle d'après, on trouve p² = 0 donc p = 0.
Avec un très grand nombre de sucres entiers au départ (peu importe celui de demi sucre), on trouve que le nombre de grand sucre va tendre vers 0, et qu'il ne restera proportionnellement que des demi-sucres.
J'espère ne pas m'être trompé dans mon raisonnement et mes calculs...
#10 - 09-06-2020 18:35:04
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
Beghi Say
Le problème se situe ailleurs, je crois.
Il est assez évident que, avec beaucoup de morceaux, le rapport entre 1/2 morceaux et morceaux entiers va tendre vers 1. Ce qui est demandé, c'est ce qu'il se passe juste avant le final.
On peut avoir une idée de la solution avec un bête tableur, la formulation est assez simple. Pour 300 morceaux, je suis arrivé à une proba de près de 0,88 pour le 1/2 morceau. Donc net avantage pour lui. Ce n'est pas intuitivement évident, qu'avec beaucoup de morceaux on donne plus de chance d'avoir 2 demis plutôt qu'un entier sur le final.
On peut toutefois observer sur tableur que la ligne qui joint les cases égalitaires (autant de 1/2 que de 1 ) a une pente 2, alors que la répartition sur ces cases a une pente 1 : La proba est alors plus favorable pour les 1/2.
Le plus incertain est la limite. Je pencherais bien pour 1, mais sans aucune certitude.
#11 - 09-06-2020 19:58:05
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
Beghi nSay
J'ai quand même bien l'impression que ma démonstration est bonne si la limite existe...
Peut-être mon schéma n'est-il pas clair :
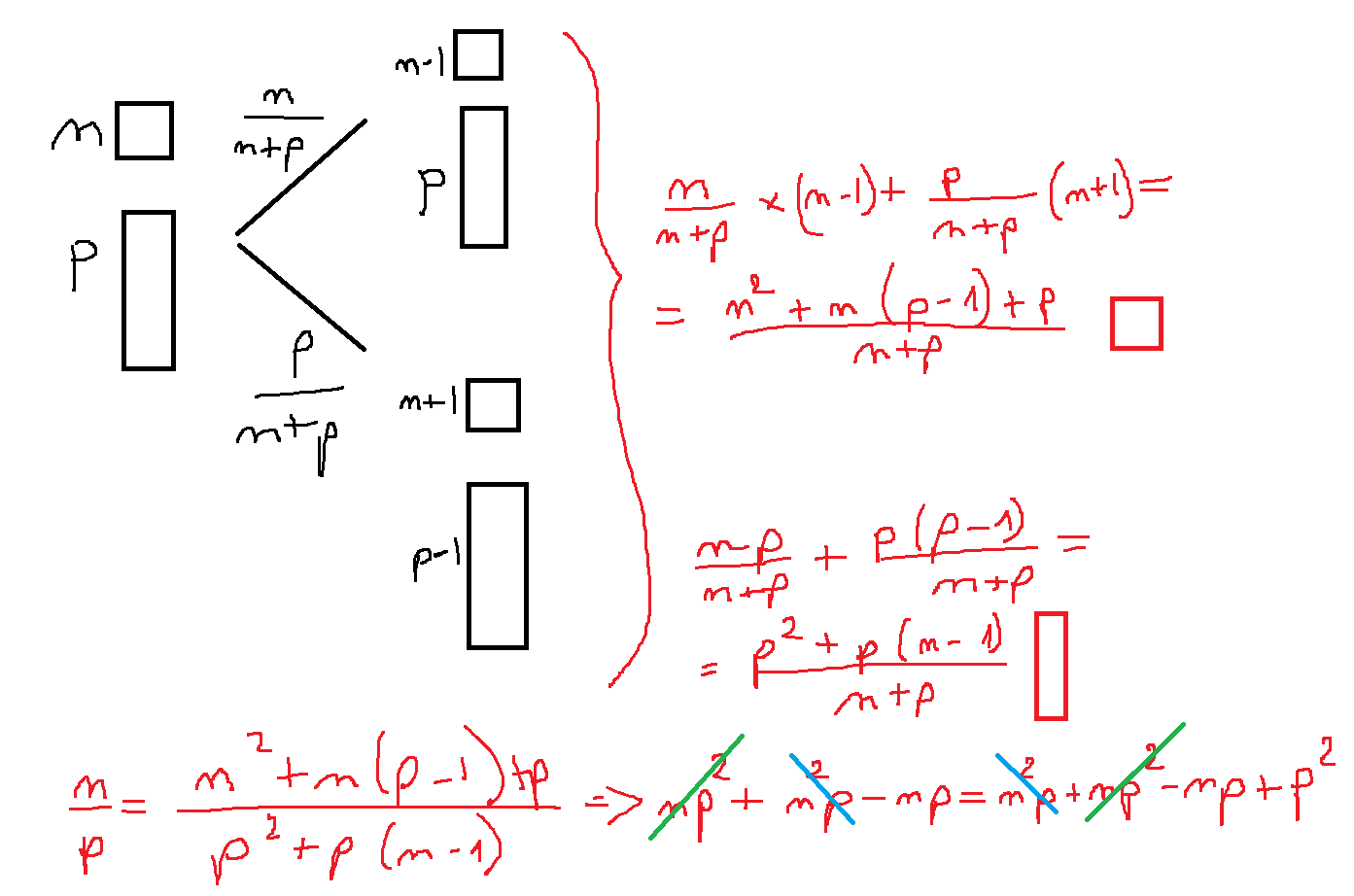
Au départ j'ai pris n demi-sucres et p sucres entiers.
*On a n/(n+p) chance de piocher un demi sucre dans la boîte. Il nous reste alors n-1 demi sucre et p sucres entiers
*On a p/(n+p) chance de prendre un sucre entier. Il nous reste alors n+1 demi-sucre et p-1 sucres entiers.
L'espérance du nombre de demi sucre après prélèvement vaut donc [n/(n+p) * (n-1)] + [p/(n+p) * (n+1)]. C'est à dire [n²+n(p-1)+p] / (n+p).
De même l'espérance du nombre de sucres entiers vaudra [p²+p(n-1)] / (n+p)
Si on considère qu'avec le temps, après un nombre de prélèvement suffisamment grand, la proportion de sucre entiers par rapport aux demi-sucres tend vers un rapport stable, alors on trouve que le rapport avant et après tirage doit rester stable.
Le rapport n/p doit donc être égal à [n²+n(p-1)+p] / [p²+p(n-1)], ce qui après simplification donne p = 0 (et aucune indication sur n).
J'ai quand même l'impression que cela prouve que pour un très grand nombre de sucre entiers au départ ces derniers vont finir par disparaître (si une limite pour la proportion est atteinte).
Qu'est-ce qui ne va pas dans ce raisonnement ?
#12 - 10-06-2020 08:57:18
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
veghin say
2 choses ne vont pas :
- En quoi le fait d'avoir un rapport limite pour un grand nombre de morceaux te donne t'il une information sur ce qu'il se passe à l'avant dernier tirage ? Bon, tu trouves par chance p = 0, ce qui te fait dire que, évidemment, si p = 0 pour un grand nombre, alors p = 0 aussi sur la fin. Mais p = 0 pour un grand nombre, c'est tout simplement absurde !
- Si p = 0 dans ton équation, il y a un souci, puisque les 2 dénominateurs de ton équation sont à 0, c'est plutôt gênant.
#13 - 10-06-2020 09:33:16
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
Behin Say
OK, je comprends mieux ce qui te dérange. Je vais réfléchir pour voir si je ne parviens pas à résoudre le point n° 1. C'est sûr que dire que si je suppose que p est très grand, alors p=0, c'est un problème...
En revanche, pour ton point 2 il suffit de calculer p/n au lieu de n/p et il n'y a plus de dénominateur nul.
#14 - 10-06-2020 13:52:29
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
Beghin Sa
Pas sûr de trouver quoi que ce soit d'intéressant...
J'ai utilisé le tableur comme toi et j'ai trouvé en démarrant avec uniquement des sucres entiers :
Avec 10 sucres : 81,41% de chance d'avoir un demi sucres en avant dernier
100 sucres : 87,1%
300 : 88,78%
500 : 89,42%
1000 : 90,18%
...
Ca fleure bon le 100% avec un grand nombre au départ, mais pas de démo en vu...
Edit : Un petit programme python me donne :
Spoiler : [Afficher le message]
u=0
u1=u
v1=100000000
v=v1
for i in range(1,2*v1):
u1=u
u=(u*(u-1)+v*(u+1))/(v+u)
v=(u1*v+v*(v-1))/(u1+v)
print((1-v/u)*100)
10.000 : 92.08%
100.000 : 93.36%
1.000.000 : 94.27%
10.000.000 : 94.97%
#15 - 10-06-2020 19:50:57
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
Beghin Sa
Voilà, la limite doit être 1.
Ce n'est pas intuitif du tout ce résultat, j'ai trouvé, d'où la présentation ici. J'ai vu cette question posée sur un site voisin, l'auteur est un mec balèze, il n'avait aucun justificatif.
Merci pour la participation.
#16 - 14-06-2020 00:27:51
- enigmatus
- Expert de Prise2Tete
- Enigmes résolues : 0
- Messages : 561
beghun say
Bonsoir,
@golgot59 :
Je suis d'accord avec les valeurs que tu obtiens en #9 pour 1, 2, 3 ou 4 sucres, mais pas avec celles qui correspondent à ton programme en #14.
Première colonne : nombre de sucres entiers au départ (et 0 demi-sucre)
Deuxième colonne : calcul exact en fractions rationnelles (long et consommateur de mémoire). La valeur est convertie en flottant pour l'impression.
Troisième colonne : calcul en flottant (beaucoup plus rapide, concorde avec la valeur précédente pour les petites valeurs de N, il pourrait y avoir des erreurs d'arrondi pour les grandes valeurs).
Quatrième colonne : résultats du programme de golgot en #14
Quant à la limite de la probabilité lorsque N tend vers l'infini, c'est difficile d'être affirmatif. La croissance est de toute façon très lente.
#17 - 14-06-2020 09:32:12
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
Beghinn Say
Je suis d'accord, il n'est pas du tout certain que la limite soit 1. On ne sait pas la calculer.
Ce que j'ai pu remarquer :
Vers 300 sucres, la dérivée première (écart entre 2 valeurs successives) est de l'ordre de 10^-5.
La dérivée seconde est de l'ordre de -10^-7.
La dérivée 3ème est de l'ordre de -10^-9.
etc....
Par ailleurs, l'utilisation des moyennes successives, qui permet évidemment d'accélérer le calcul, ne garantit pas l'exactitude du résultat, à mon sens.
#18 - 14-06-2020 13:19:53
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
beghin sat
Exact enigmatus, mon programme ne fonctionne pas. J'ai oublié les cas ou un type de sucre est absent. Désolé. Je vais voir si je peux corriger ça.
Sinon je suis aussi d'accord avec vos observations.
#19 - 15-06-2020 09:39:34
- Migou
- Expert de Prise2Tete
- Enigmes résolues : 17
- Messages : 644
- Lieu: Ville 2/N près 2*i
beghib say
Bonjour, je vois des probabilités qui tendent vers un. Mais pour moi, la répartition entre nombre de sucres et de demi-sucres doit tendre vers 50%-50%.
Argument : si le nombre de demi-sucres est plus important, il est plus probable d'en tirer un donc la proportion de demisucres baisse en moyenne. Inversement, si le nombre de demi-sucres est moins importante que celle de sucres, il est plus probable de tirer un sucre entier et la proportion de demi-sucres augmente.
Je m'attends donc à du 50/50.
#20 - 15-06-2020 10:52:46
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
Beghin Sayy
C'est précisément parce que le résultat est totalement contre-intuitif que j'ai présenté cette question. Le fait que la limite est proche de 1 ( très proche de 0,95 pour l'instant ) n'est plus à remettre en question, il y a recoupements de calculs indépendants qui conduisent tous à ce résultat. Ce qu'on ne sait pas faire pour l'instant, c'est calculer cette limite de façon précise.
#21 - 15-06-2020 11:08:02
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
beghib say
Salut Migou !
Prendre un demi-sucre enlève juste un demi-sucre alors qu'en prendre un entier en enlève un entier mais ajoute aussi un demi-sucre dans la boîte.
Du coup la proportion de demi-sucre dans la boîte augmente avec les prélèvements.
Perso ma première intuition était une limite qui aurait tendue vers 1/3 2/3 en faveur des demi-sucres pour la raison que tu évoques : Une fois stabilisé, il y aurait eu 2 fois plus de chances de prélever un demi-sucre qu'un sucre, mais puisque prendre un entier en rajoute un demi, ça "compensait".
Les calculs montre très rapidement qu'il n'en est rien...
(Encore une fois, on se rend mieux compte du phénomène en l'exagérant : Si dans une boîte tu as des plaques de chocolat composées chacune de 24 petits carrés, et que lorsque tu en prélèves une, tu ne manges qu'un carré et que tu remets dans la boîte les 23 restants un par un, le raisonnement du 50/50 ne tient plus.)
#22 - 16-06-2020 01:51:34
- Sydre
- Professionnel de Prise2Tete
- Enigmes résolues : 15
- Messages : 245
behhin say
A mon avis l'astuce de base est de représenter le problème sous la forme d'un arbre de probabilités cyclique. Après c'est "juste" une histoire de calcul.
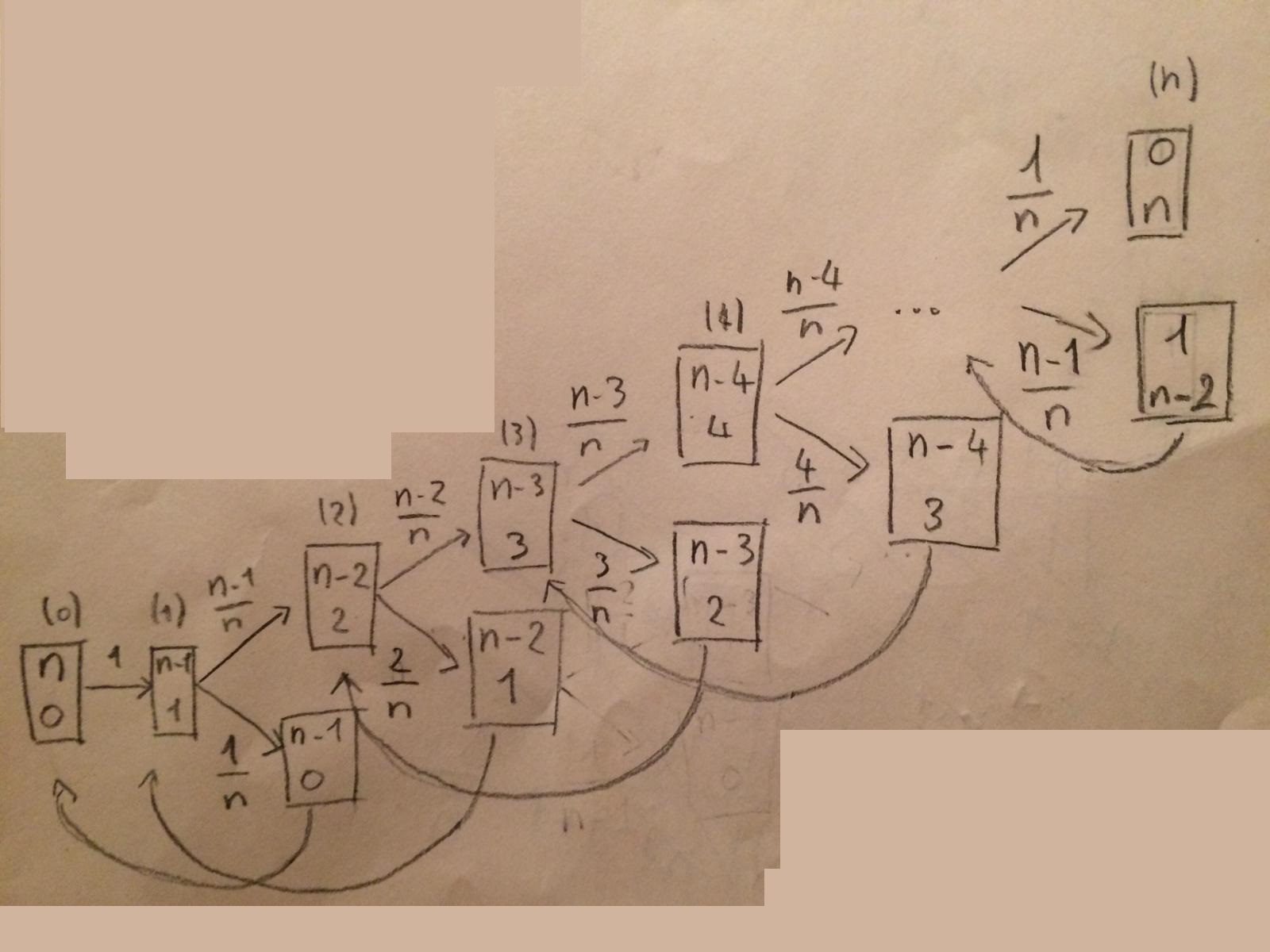
Pour élaborer un peu de mon coté ça donne :
Probabilité d'arriver au nœud i de la branche supérieure en partant du nœud 0 :
Sni=(n−1)!(n−i)!ni−1
Probabilité d'arriver au nœud i de la branche supérieure en partant du nœud j :
Sni→j=SnjSni
Probabilité de boucler après le nœud i :
Bni=1−Sni+1Sni
Probabilité d'avoir un sucre entier la veille :
Pn=n−1∑a=1(Sn1→aBna(n−2∑b=a−1Sn−1a−1→bBn−1b(…)))
Explicitons Sni→jBnj :
Sni→jBnj=SnjSni(1−Snj+1Snj)=Snj−Snj+1Sni
Ce qui conduit à :
Pn=1Sn1n−1∑a=1(Sna−Sna+1Sn−1a−1(n−2∑b=a−1Sn−1b−Sn−1b+1(…)))
Or Sn1=1 et explicitions Sna−Sna+1Sn−1a−1 :
Sna−Sna+1Sn−1a−1=(n−1)!(n−a)!na−1−(n−1)!(n−a−1)!na(n−2)!(n−a)!(n−1)a−2=(n−1n)a−1an
Ce qui conduit à :
Pn=1nn−1∑a=1((n−1n)a−1a(n−2∑b=a−1Sn−1b−Sn−1b+1(…)))
En développant jusqu'au bout on obtient :
Pn=2n!n−1∑a=1n−2∑b=a−1…2∑y=x−1((n−1n)a−1(n−2n−1)b−1…(23)y−1ab…y(S21−S22))
Or S21−S22=12 et par conséquent :
Pn=1n!n−1∑a=1n−2∑b=a−1…2∑y=x−1((n−1n)a−1(n−2n−1)b−1…(23)y−1ab…y)
Je n'ai pas poussé le calcul plus loin pour l'instant mais on doit sans doute pouvoir encore simplifier, ou au moins démontrer que lim à partir de cette dernière expression. La suite à plus tard 
Quelques rapides vérifications :
A la main on trouve P_2=\frac{1}{2}, P_3=\frac{7}{18} et P_4=\frac{97}{288}.
En utilisant la formule on retrouve bien :
P_2=\frac{1}{2!}=\frac{1}{2}
P_3=\frac{1}{3!}\sum_{a=1}^2\left(\frac{2}{3}\right)^{a-1}a=\frac{7}{18}
P_4=\frac{1}{4!}\sum_{a=1}^3\sum_{b=a-1}^2\left(\frac{3}{4}\right)^{a-1}\left(\frac{2}{3}\right)^{b-1}ab=\frac{97}{288}
#23 - 16-06-2020 10:47:34
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1971
Beghin Saay
Il y avait un projectEuler où un papetier coupait une feuille jusqu'à obtenir la bonne taille et remettait les chutes, ça ressemblait.
Tu peux résoudre facilement avec un processus de Markov : considérant le nombre de sucres et de demi-sucres tu as une matrice quasiment pleine de zéro et qui de toutes les façons atteindra sa limite au 2Nième tour par construction
On peut aussi le faire en dynamique programming. Tu peux donc connaitre chaque probabilité en passant à l'étape d'après en temps linéaire - c'est même beaucoup plus efficace.
En effet, la matrice est de l'ordre de N^2 sur N^2, et donc sa puissance 2N-2ème sera de l'ordre de O(N^4,752.log(N)) - et en DP juste en O(N^2)
#24 - 16-06-2020 15:17:12
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1971
#25 - 17-06-2020 09:46:55
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1971
Beghin Sa
golgot59 a écrit:mon programme ne fonctionne pas. J'ai oublié les cas ou un type de sucre est absent.
A mon sens a complexité est en N². Ton code est en O(N), et franchement si tu arrives à le faire marcher c'est très intéressant !
En O(N²) le dernier résultat met une dizaine de minutes à sortir avec mon code
10: 0.761443
100: 0.857820
1.000: 0.896716
10.000: 0.918266
100.000: 0.932128
On verra pour le million demain 
En tous les cas, c'est une suite qui semble croissante (et en plus bornée, donc il existe forcément une limite si la croissance peut être prouvée)
|
 |

 Accueil
Accueil
 Forum
Forum








