 |
#1 - 20-10-2023 19:11:08
- aunryz
- Elite de Prise2Tete
- Enigmes résolues : 17
- Messages : 1074
- Lieu: Nicastro / Tronville
Pur obtenir un carré
(précision supplémentaire le 21/10)
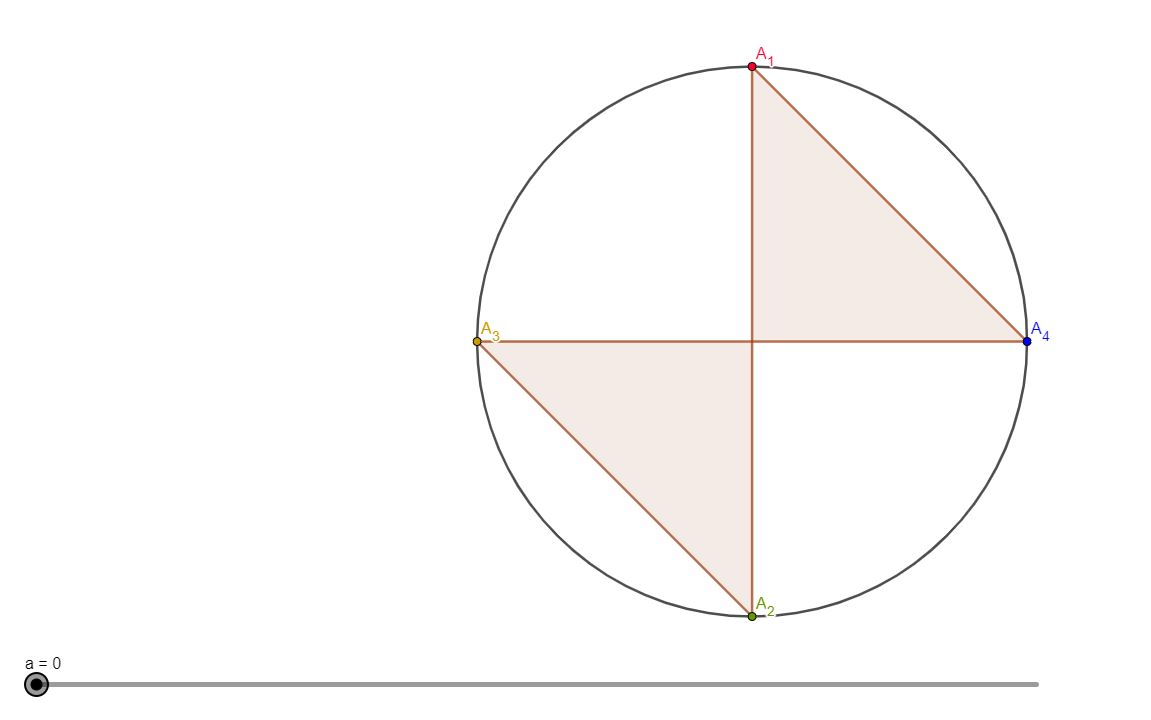
A quelle(s) condition(s) minimales sur les vitesses relatives(Vn) des points An (relation qui les lie) obtiendra-t-on un carré à partir de la figure de départ, les points se déplaçant sur le cercle à vitesse constante.
Dans cet exemple (animation), avec les vitesses données, on ne parvient pas à un carré
la figure boucle quand le curseur est sur 36000, après avoir fourni
deux demi-carrés opposés
et
un évanouissement.
L'animation se met en route en cliquant sur le petit symbole en bas à gauche (lecteur)
le lien :
https://www.geogebra.org/classic/kpfxpqsr
Lélio Lacaille - Du fagot des Nombreux
#2 - 21-10-2023 10:45:46
- Migou
- Expert de Prise2Tete
- Enigmes résolues : 17
- Messages : 642
- Lieu: Ville 2/N près 2*i
pour obtenir un catré
Salut Aunryz,
Tu penses à une condition nécessaire ou suffisante ?
#3 - 21-10-2023 20:11:05
- aunryz
- Elite de Prise2Tete
- Enigmes résolues : 17
- Messages : 1074
- Lieu: Nicastro / Tronville
PPour obtenir un carré
Merci Migou de m'aider à préciser
Il s'agit des conditions minimales sur les vitesses des points An
pour obtenir, à un instant donné de la rotation de ces points
un carré parfait.
De même qu'ici avec les vitesses données
on obtient par deux fois
un triangle isocèle rectangle
(mais jamais de carré)
Lélio Lacaille - Du fagot des Nombreux
#4 - 22-10-2023 08:28:03
- clanelle
- Passionné de Prise2Tete
- Enigmes résolues : 0
- Messages : 77
PPour obtenir un carré
Bonjour,
Je ne suis pas certain de bien comprendre, mais si on devait toujours tout comprendre pour se lancer, je ne me lancerais jamais 
Si je donne une vitesse quelconque à A1 et une vitesse opposée à A4, en laissant A2 et A3 à leur position de départ (vitesse = 0), j'obtiendrai que A1 et A4 échangent leurs positions respectives.
S'il s'agit de trouver l'impulsion minimale, alors je donne la plus petite impulsion possible à A1 et à A4 (en sens opposé).
Mais a-t-on le droit au sens opposé ?
Bien cordialement,
Lionel
#5 - 22-10-2023 23:40:14
- Migou
- Expert de Prise2Tete
- Enigmes résolues : 17
- Messages : 642
- Lieu: Ville 2/N près 2*i
Pour obteenir un carré
soient (θ1,θ2,θ3,θ4) les coordonnées angulaires initales (en quart de tour pour simplifier les calculs) de A1, A2, A3 et A4 = (0, 2, 1, 3). et v1,v2,v3,v4 les vitesses angulaires (en quart de tour/s)
Pour faciliter les calculs, on fixe A1 au point de coordonnées (1,0) et on note v'2,v'3,v'4 les vitesses angulaires relatives de A2..A4 par rapport à A1, c'est à dire v′i=vi−v1
Il y a deux façons de former un carré : soit le carré se forme avec A1 A2 A3 A4 dans le sens horaire, soit dans le sens horaire, soit dans le sens anti-horaire, dit aussi sens direct ou trigonométrique.
Petit dessin de la position de départ :
A3
|
A2 --+-- A1
|
A4
Prenons par exemple le cas du sens trigonométrique.
A2 se trouvera à sa place à chaque temps ci=3+4iv′2 et ce quelle que soit la valeur de v′2
Reste à choisir les vitesses angulaires v′3 et v′4 pour cela, on peut fixer la valeur de i à sa convenance. Et on aura un carré ssi
v'_3.c_i = \frac{v'_3.(3+4i)}{v'_2} \equiv 1 \pmod 4
et
v'_4.c_i = \frac{v'_4.(3+4i)}{v'_2} \equiv 0 \pmod 4
Que peut-on en conclure ? Je ne vois pas trop.
D'abord, qu'il y a tout un tas de solutions.
Je peux dire qu'une condition nécessaire à la formation du carré est que le rapport entre deux vitesses angulaires relatives soient rationnelles.
#6 - 23-10-2023 22:52:52
- aunryz
- Elite de Prise2Tete
- Enigmes résolues : 17
- Messages : 1074
- Lieu: Nicastro / Tronville
Pur obtenir un carré
Oui, Migou il y a des tas de solutions et ton approche le montre
Bien parti clanelle : mais considérons que les vitesses ne sont acceptées que positivement (au sens large) donc mouvement sinistrogyre.
Ceci dit, il y a dans ta proposition un élément qui permet de simplifier effectivement le problème.
Disons que l'on recherche la solution la plus "simple" ("économique")
La relation entre les vitesses qui utilise des nombres (positifs) dont la somme est minimale.
Merci Migou et clanelle d'avoir aidé à préciser la question.
Lélio Lacaille - Du fagot des Nombreux
#7 - 25-10-2023 08:59:47
- Migou
- Expert de Prise2Tete
- Enigmes résolues : 17
- Messages : 642
- Lieu: Ville 2/N près 2*i
Pour oobtenir un carré
A3
|
A2 --+-- A1
|
A4
une solution évidente pour les vitesses angulaires (toujours en quart de tour par s est (v1..v4) = (-1, 0, 0, +1), ce qui aura pour effet de permuter A1 et A4.
A3
|
A2 --+-- A4
|
A1
Pour donner des vitesses positives, on peut ajouter une vitesse de rotation arbitraire de +1, identique à tous les points.
(v1..v4) = (0, 1, 1, 2)
#8 - 25-10-2023 14:56:58
- aunryz
- Elite de Prise2Tete
- Enigmes résolues : 17
- Messages : 1074
- Lieu: Nicastro / Tronville
Pour oobtenir un carré
Oui Migou
Ta réponse avec valeur négative rejoint celle de clanelle
et
effectivement on peut l'utiliser pour trouver une solution ne comportant que des valeurs positives
Celles que tu donnes sont effectivement très simples.
Spoiler : [Afficher le message] https://www.geogebra.org/geometry/zkt6vpnh
Ceci dit
tu peux aussi déduire de ta première étape une solution pour laquelle les points immobiles le demeurent, en utilisant ce que tu as donné dans ta première approche
à savoir que les valeurs s'entendent modulo 4.
____
PS: une question : comme je suis identifié comme l'auteur du script j'y accède et peux le modifier. Est-ce qu'en cliquant sur le lien, vous avez eu accès dans la page d'énoncé, à l'animation ?
Lélio Lacaille - Du fagot des Nombreux
#9 - 26-10-2023 16:19:21
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3230
- Lieu: Luxembourg
Pour obtenr un carré
Le lien va bien sur GeoGebra, mais la mention "non autorisé" apparait et l'animation ne se lance pas.
#10 - 26-10-2023 16:41:07
- aunryz
- Elite de Prise2Tete
- Enigmes résolues : 17
- Messages : 1074
- Lieu: Nicastro / Tronville
Pour otbenir un carré
Franky1103 a écrit Le lien va bien sur GeoGebra, mais la mention "non autorisé" apparait et l'animation ne se lance pas.
Merci de ton retour
j'ai vérifié sur une tablette où je ne suis pas connecté,
à présent cela devrait fonctionner.
Lélio Lacaille - Du fagot des Nombreux
#11 - 26-10-2023 18:18:05
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3230
- Lieu: Luxembourg
pour obrenir un carré
Salut,
Sans pénaliser la généralité de l’énigme, je peux considérer que le point A4 est immobile (ou, si on préfère, que le référentiel tourne à la vitesse opposée à celle de A4).
Les points A1, A2 et A3 sont initialement situés par rapport à A4 à respectivement ¼, ½ et ¾ de tour et ils ont respectivement une vitesse (en tours par unité de temps) de V1, V2 et V3.
Pour les positions finales (au temps T) de ces points, on aura alors six cas à étudier (k1; k2 et k3 sont des nombres entiers):
1°) A1, A2 et A3 reviennent à leurs positions initiales
V1.T = k1; V2.T = k2; V3.T = k3
=> V2 = V1.k2/k1 et V3 = V1.k3/k1
2°) A1 revient à sa position initiale et A2 / A3 intervertissent leurs positions
V1.T = k1; V2.T = k2+¼; V3.T = k3-¼
=> V2 = V1.(k2+¼)/k1 et V3 = V1.(k3-¼)/k1
3°) A2 revient à sa position initiale et A1 / A3 intervertissent leurs positions
V1.T = k1+ ½; V2.T = k2; V3.T = k3-½
=> V2 = V1.k2/(k1+½) et V3 = V1.(k3+½)/(k1+½)
4°) A3 revient à sa position initiale et A1 / A2 intervertissent leurs positions
V1.T = k1+¼; V2.T = k2-¼; V3.T = k3
=> V2 = V1.(k2-¼)/(k1+¼) et V3 = V1.k3/(k1+¼)
5°) A1 vient en A2, A2 vient en A3 et A3 vient en A1
V1.T = k1+¼; V2.T = k2+¼; V3.T = k3-½
=> V2 = V1.(k2+¼)/(k1+¼) et V3 = V1.(k3-½)/(k1+¼)
6°) A1 vient en A3, A2 vient en A1 et A3 vient en A2
V1.T = k1+½; V2.T = k2-¼; V3.T = k3-¼
=> V2 = V1. (k2-¼)/(k1+ ½) et V3 = V1. (k3-¼)/(k1+ ½)
Mais le manque de ’’formule plus générale’’ me gêne dans mon développement.
#12 - 27-10-2023 00:23:05
- aunryz
- Elite de Prise2Tete
- Enigmes résolues : 17
- Messages : 1074
- Lieu: Nicastro / Tronville
Poru obtenir un carré
Chacun a ici donné une/des réponses qui correspond à la question posée.
La réponse la plus complète étant celle de Franky1103
(mais il ne faut conserver que les 2 et 5 pour que la figure ne soit pas un quadrilatère croisé.
On peut partir de la considération de Migou
et la réduire dans un premier temps à
Pour obtenir le carré 1234 (sens trigo)
les vitesses respectives des points A1, A2, A3 et A4 : 1;2;2;3
équivalentes à 2;3;3;0, à 3;0;0;1 et à 0;1;1;2
Pour obtenir le carré 1432 (idem)
les vitesses respectives des points A1, A2, A3 et A4 : 2;1;3;2
équivalentes à 3;2;0;3, à 0;3;1;0 et à 1;0;2;1;
La forme générale étant celle que propose Franky1103
Merci Migou, clanelle et Franky1103 de votre participation.
REM :
L'énoncé qui aurait permis des réponses plus nettes aurait été
"le cas le plus simple pour des vitesses toutes positives"
Lélio Lacaille - Du fagot des Nombreux
|
 |

 Accueil
Accueil
 Forum
Forum







