A première vue pour T=5, il existe une période de 5h pendant laquelle il a marché 20km et pour T=0 il existe une période de 0 seconde pendant laquelle il a marché 0 km.

Si on trace la courbe de la vitesse en fonction du temps, on peut tracer une bande de T heures et la faire défiler jusqu'à trouver une zone ou l'aire sous la courbe fasse 4T km.

Mathématiquement, ça donne : soit [latex]v(t)[/latex] la vitesse en fonction du temps.
On cherche si il existe [latex]t_a[/latex] et [latex]t_b[/latex] tels que [latex]\int_{t_a}^{t_b}v(t)dt = 4T[/latex].

A partir du moment ou 4T est inférieur ou égal à 20, il existera toujours un intervalle [latex](t_a,t_b)[/latex] tel que :
[TeX]\int_{0}^{t_a} f(x) dx +\int_{t_a}^{t_b} f(x) dx + \int_{t_b}^{20} f(x) dx = \int_{0}^{20} f(x) dx[/TeX]
Ma réponse est donc oui.

je pense que c'est toujours possible.
Si le marcheur marche à la moyenne de 4 km/h alors on peut définir la fonction sur [0;5] tel que f(x)=4x
Soit g la fonction décrite par le marcheur. Ce que l'on sait c'est que g(0)=0        g(5) =20 et  g est continu et toujours croissante donc la dérivé de g est toujours positive.

Montrons qu'il existera T appartenant à [0;5] tel que g'(T)>=4
Supposons que pour tout T appartenant à [0;5] g'(T)<4
On décompose l'intervalle [0;5] en n intervalles de dimention h=5/n et  on définit g sur tous les intervalle [[latex]{5k\over n};{5(k+1)\over n[/latex]] pour tout k entre 0 et n-1
alors pour tout k entre 0 et n-1 [latex]g({{5(k+1)}\over n})-g({{5k}\over n})<4h[/latex] cela veut dire que si on additionne tous les membres de l'inégalité [latex]\sum_{k=0}^{k=n-1}g({{5(k+1)}\over n})-g({{5k}\over n})<n\times 4h[/latex]c'est à dire g(5) - g(0)<20 or g(0)=0 et donc g(5) <20 ce qui est contradictoire

Donc il existera T appartenant à [0;5] tel que g'(T)>=4

Super intéressant à résoudre, surtout que l'intuition, une fois n'est pas coutume, m'a trompée.

Alors, on va commencer par définir les variables utilisées...
C = vitesse moyenne du marcheur (ici 4km/h), D = durée de la marche (5 h), L = longueur du parcours (20 km).
T = période d'observation continue sur laquelle on voudrait une vitesse moyenne = C.
P(t) : position du marcheur à l'instant t.

Première étude : si D/T est un entier n (dans le cas, T = 1 heure, n=5)

On pose f(t) = P(t) - C t, par construction f(0) = f(D)=0.
(l'étude sur f à la place de P revient à faire le problème avec une vitesse moyenne nulle).

On pose gT(t) = f(t+T) - f(t), gT est définie pour t € [0, D-T].

Résoudre le problème revient à trouver une valeur de t0 qui annule gT.

Si gT(0) = 0, alors t0=0.
Sinon, on va supposer gT(0) < 0 (toujours possible en remplaçant f par -f). Soit f(T) < 0

Supposons que pour tout t € [0;D-T], gT(t) < 0.
Donc g(T) < 0 donc f(2T) < f(T) < 0 et par récurrence f(iT) < f(iT-T) < 0.
Or f(nT)=f(D)=0 donc 0<0, c'est impossible
Donc, il existe t1 tel que gT(t1)>=0.

Par continuité entre 0 et t1, il existe t0 tel que gT(t0)=0.

Donc si T = 1 heure, ou plus généralement si T est tel que D/T est entier, alors il existe t0 tel que (P(T+t0) - P(t0))/T = C.

Seconde étude : si D/T n'est pas entier.
On pose n=E(D/T) (partie entière) et R= D-nT.

On définie le mouvement du marcheur de la façon suivante (pour i = 0 à n-1):
sur [iT;iT+T/2] : arrêt (Vit=0)
sur [iT+T/2;IT+T], Vit = Vc constante.
Et on poursuit sur [nT;nT+R] :
Si R <=T/2 : sur [nT;R] : arrêt et on pose A = 0 (on a A<R/2)
Si R >T/2 : sur [nT;nT+T/2] : arrêt et sur [nT+T/2;nT+R] : Vit=Vc et on pose A=R-T/2, soit R/2 + R/2 = T/2 + A comme R<T on a aussi A<R/2

rem : A correspond au temps de marche à vitesse Vc après nT.

Calculons Vc pour que la vitesse moyenne du parcours soit C :
C= (0 x (n x T/2 +min(R;T/2)) + Vc (n x T/2 + A))/D
donc : Vc = C D / (n * T/2 + A)

Comme nT+R= D et A<R/2, on a Vc/2 > C

Sur chaque période I de temps de durée T, on a exactement T/2 temps d'arrêt et T/2 temps de marche à la vitesse Vc, la vitesse moyenne sur I est Vc/2 (> C).

Pour le déplacement que nous avons construit, Il n'y a donc aucune période de durée T sur laquelle la vitesse moyenne est la vitesse moyenne du parcours total.

Et comme un petit dessin vaut mieux qu'un long disours, voici pour T=0,88 h :

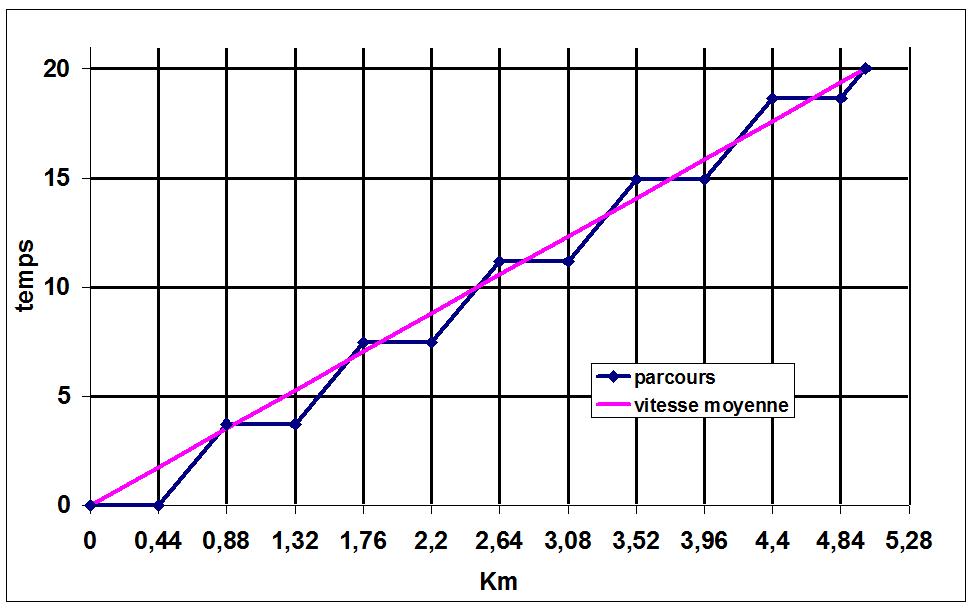
oup ! le lecteur attentif aura corrigé de lui même : en X le Temps et Y les km

Je me permets humblement de commenter les réponses faites :

EfCEba a tout à fait raison : on va trouver ta et tb pour que la vitesse moyenne de ta à tb soit égal à 4T. Par contre, rien ne dit que tb - ta = T, donc ça ne répond pas à la question !

Gabriel montre qu'on va trouver T pour que la vitesse moyenne pendant un temps T soit égale à 4T, mais la question n'est pas là : T est fixé et il faut le placer sur le parcours. Ou alors j'ai pas tout compris !

Vasimolo et Scarta montrent que pour T=1 heure, il y aura un intervalle où la vitesse moyenne sera égale à la vitesse moyenne du parcours total. Très bien.

Par contre : pour T quelconque, on ne trouvera pas forcement d'intervalle de ce type (voir mon exemple).

Pour ddpm Existe-t-il nécessairement une période continue de 2 heures durant laquelle il a parcouru 8 km ? , oui, car d = 4t ?

Je ne suis pas convaincu car il faut raisonner sur les heures ( pas sur les distances ) et 2 ne divise pas 5 . Je te donnerai un contre-exemple demain si tu n'es pas convaincu d'ici là .

Vasimolo

Bonjour,

Pour dylasse :
"Cette formule n'est valable que si les 2 trajets aux vitesses V1 et V2 sont réalisés sur la même distance (exemple aller-retour)."
Oui, en effet je suis allé un peu vite, mais le résultat d=4t est toujours valable (Pas le temps de voir pourquoi !).
Plus simplement :
Si il existe une période de temps t durant laquelle il aura marché 4t => d=4t (Comme avant...)...

"Seconde étude : si D/T n'est pas entier."
Une période de temps t durant laquelle il aura marché 4t
Oui car D/T = 4

Pour Vasimolo :
"Je ne suis pas convaincu car il faut raisonner sur les heures ( pas sur les distances )"
Je ne comprends pas : La vitesse moyenne, les heures et les distances sont liées ?
"Existe-t-il nécessairement une période continue de 2 heures durant laquelle il a parcouru 8 km ?"
Pour moi :
Vm= 4km/h = Vitesse moyenne du parcours
V1 = 12/3 = 4km/h
d=12km t=3h => 1 période de 3 heures sur 12 km à la Vitesse moyenne de 4km/h
V2 = d/t => v2 = 8/2 = 4km/h
d=8km t=2h => 1 période de 2 heures sur 8 km à la Vitesse moyenne de 4km/h

Note :
Je ne passe ici qu'occasionnellement (Souvent absent, pas beaucoup de temps..) pour me distraire, c'est pourquoi je ne peux participer régulièrement.
Encore merci pour vos énigmes.