yeah je viens de comprendre l'énoncé

J'opte pour la soucoupe transparente avec indication du centre. Là, je sais faire des rosaces depuis belle lurette

Bonjour

Après avoir tracé le cercle "de base" avec la soucoupe, on trace avec le même gabarit un cercle extérieur tangent en A au cercle de base.
Puis on continue en continuant de tracer successivement des cercles extérieurs tangents à la fois au cercle de base et au cercle extérieur précédemment tracé.

Le quatrième cercle extérieur (en comptant le premier) ainsi tracé est tangent au cercle de base au point "soucoupement opposé à A"     

Bonne journée
Nicolas

bonjour
autour d'un cercle de diametre a, on peut placer exactement 6 cercles adjacents à celui ci et qui son adjacents entre eux, donc pour obtenir le point diametralement opposé au tien, il faut:
-tracer le premier cercle
-placer le point A
-tracer un second cercle adjacent au premier en A
-tracer un troisieme adjacent au 2 premiers
-un quatrieme adjacent au 1er et au dernier
-un cinquieme adjacent au quatrieme et au premier, pile poil diametralement opposé à A


ou sinon, si on a plusieurs soucoupes de taille identique, on les pose cote à cote comme je l'ai décrit (je sais pas si c'est clair,mais ça l'est dans ma tête)

bonne journée

alors d'accord si on ne peut pas tracer de cercler adjacent sans compas, comment on trouve le centre d'un cercle tracé avec une soucoupe sans instrument? je veux bien une liste du matos auquel on a droit avant de poursuivre ma reflexion

Un dernier indice a été ajouté ( et pratiquement la réponse ) .

Une solution sans difficulté particulière mais quasiment hors d'atteinte tant elle s'éloigne de nos habitudes : à méditer

Vasimolo

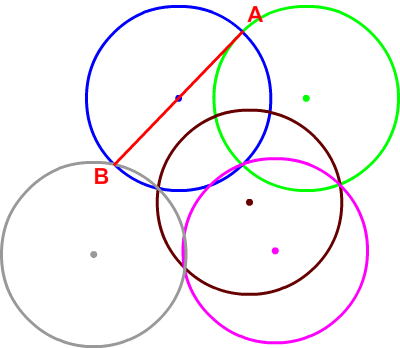
On va d'abord montrer que pour 2 cercles $C_a$ et $C_b$ de même rayon R, de centres $O_a$ et $O_b$, et sécants en 2 points $M_1$ et $M_2$, on a $\vec{O_aM_1}$ = $\vec{M_2O_B}$
Tout d'abord, $O_a$ (tout comme $O_b$) est sur la médiatrice de [$M_1$$M_2$], puisque $O_aM_1 = O_aM_2 = O_bM_1 = O_bM_2 = R$
Donc le quadrilatère $O_aM_1O_bM_2$ a d'une part 4 côtés égaux, et d'autre part des diagonales qui se coupent en angles droits, c'est donc un losange et de ce fait $\vec{O_aM_1} = \vec{M_2O_B}$



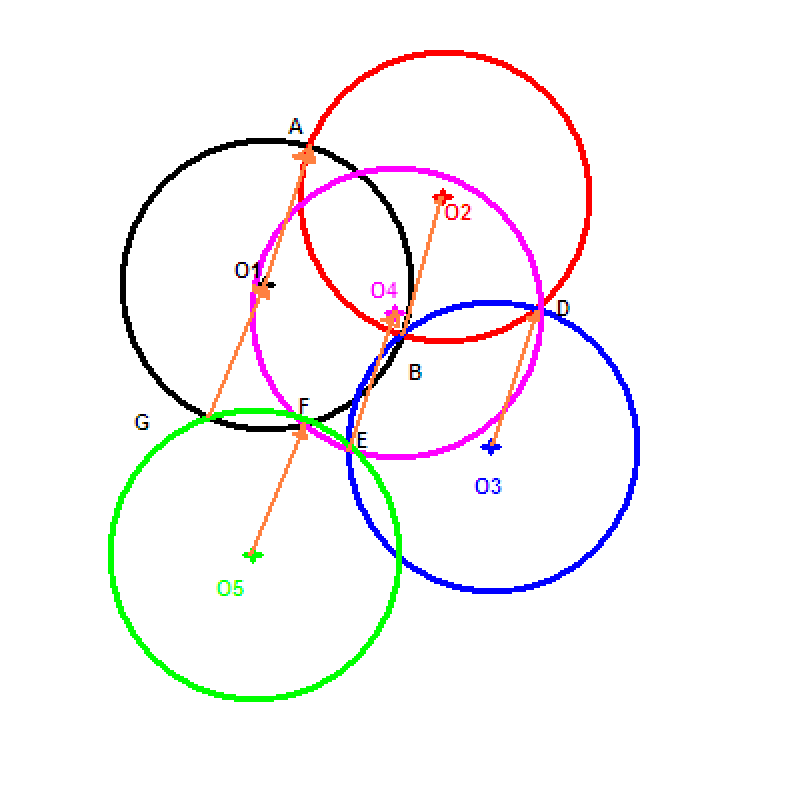
On construit un premier cercle $C_1$ de centre $O_1$, et on place un point A sur ce cercle.
On construit ensuite un cercle $C_2$ de centre $O_2$ qui coupe $C_1$ en A et en un autre point B, $\vec{O_1A} = \vec{BO_2}$
On construit ensuite un cercle $C_3$ de centre $O_3$ qui coupe $C_1$ et $C_2$ en B et $C_2$ en un autre point D, $\vec{BO_2} = \vec{O_3D}$
On construit ensuite un cercle $C_4$ de centre $O_4$ qui coupe $C_2$ et $C_3$ en D, $C_3$ en un autre point E, et enfin qui coupe $C_1$ en F $\vec{O_3D} = \vec{EO_4}$
On construit enfin un cercle $C_5$ de centre $O_5$ qui passe par E et F. Il coupe $C_1$ une seconde fois en G.
Il coupe donc $C_3$ en E, $C_4$ en E et F, et $C_1$ en F et G. $\vec{EO_4} = \vec{O_5F}$ d'une part et $\vec{O_5F} = \vec{GO_1}$ d'autre part.

Au final, $\vec{O_1A} = \vec{GO_1}$ donc [AG] est un diamètre de $C_1$

Bonne réponse de scarta et dhrm77 mais je refuse celle de FRiZMOUT qui n'a pratiquement rien fait que copier et qui se permet en plus de s'autocongratuler

J'aurais sûrement dû ajouter une étape avant la dernière en indiquant qu'il ne restait plus qu'un cercle à construire !!!

J'espère quand même que l'exercice vous a plu

Vasimolo

Pourquoi faire simple quand on peut faire compliqué!Spoiler : [Afficher le message] il suffit tous simplement de leur apprendre notre technique et dans 2 ou 3 millions d'années tu reposes le même problème et on fera avec la leur mais on ne sera certainement plus qu'a la base s'eût été la nôtre!