Forum dédié aux énigmes et à toutes formes de jeux de logique. | Déconnexion |
|
Tu n'es pas identifié sur Prise2tete : s'identifier.  Accueil Accueil
 Forum Forum
|
 |
#1 - 10-01-2011 18:17:42
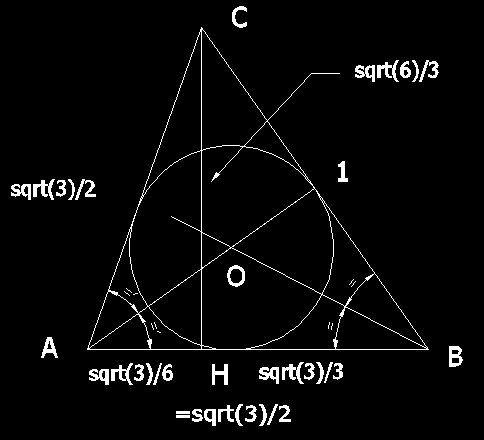
Qui sera le pharaon ed la géométrie ?On place une sphère de rayon 1 dans un tétraèdre régulier de façon à ce qu'elle soit tangente aux trois faces issues du sommet. C'est à l'intelligence d'achever l'oeuvre de l'intuition.
#0 Pub#2 - 10-01-2011 19:13:12
Qui sera le pharaon dee la géométrie ?La formule donnant le rayon de rayon de la sphère inscrite à un tétraèdre régulier est r=h/4 où h est la hauteur du tétraèdre. La distance que l'on cherche est donc 4-1=3. La paix dans le monde n'est pas menacée par les révoltés, mais par les soumis. Georges Bernanos #3 - 12-01-2011 09:57:54#4 - 12-01-2011 13:14:48
qui sera le pharain de la géométrie ?ça serait pas 3 ? #5 - 13-01-2011 14:08:26
qui sera lr pharaon de la géométrie ?Le centre de la sphère de rayon 1 se trouve à √3≈1.7 du sommet des trois faces à la quelle elle est tangente. The proof of the pudding is in the eating. #6 - 13-01-2011 19:15:28#7 - 13-01-2011 20:01:52
Qui sera l pharaon de la géométrie ?Bah, Google => sphère inscrite tétraèdre régulier => 3ème lien... La paix dans le monde n'est pas menacée par les révoltés, mais par les soumis. Georges Bernanos #8 - 13-01-2011 20:31:40#9 - 13-01-2011 20:38:29
Qui sera le pharaon de la géométrie
Ok j'ai vu... tu fais confiance à ce genre de page ? Et puis la typographie est tellement pourrie que je n'aurais même pas pris la peine de la lire en détail :-) #10 - 13-01-2011 21:16:06
Qui sera lle pharaon de la géométrie ?
Bah, c'est pas non plus pour envoyer des hommes sur la lune hein ! La paix dans le monde n'est pas menacée par les révoltés, mais par les soumis. Georges Bernanos #11 - 13-01-2011 21:53:58
qui sera le pharaon de la héométrie ?Ah parce qu'EN PLUS tu fais confiance à SaintPierre quant à l'utilisation de nos calculs ??? Réponse rapideSujets similaires
Mots clés des moteurs de recherche |
 | |||||||||||||||||||||||||||||||||
| Prise2Tete Forum Statistiques Liste des membres Hall of Fame Contact | |||||||||||||||||||||||||||||||||||
Un jeu où seules la réflexion, la logique et la déduction permettent de trouver la solution.