On trace AB puis une droite quelconque passant par A, puis à l'équerre la perpendiculaire à cette droite passant par B, on a le point C, puis la perpendiculaire à BC passant par B, puis la perpendiculaire passant par A qui détermine E, le segment CE coupe AB au milieu.

Au compas on reporte la distance AC pour trouver A', A'E coupe AB au tiers de sa longueur en F, on reporte BF au compas pour trouver B'.

Est-ce minimal ?, je ne sais pas.

Question n°1 :

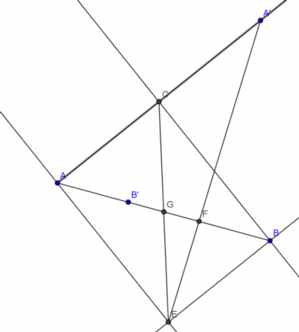
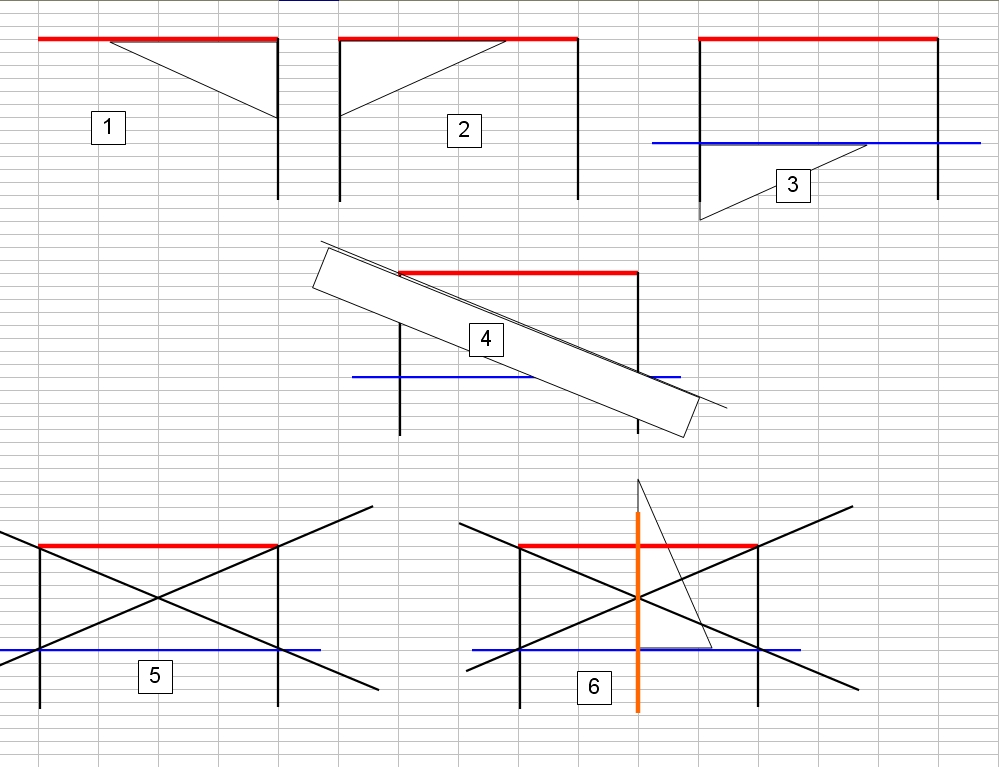
On trace un segment [AB] grâce à la règle non graduée.
Ensuite, avec un des angles non droits de l'équerre, on trace une demi-droite [Ax). Avec le deuxième angle non droit, on trace une deuxième demi-droite [By) "du même côté".
Ces demi-droites se coupent en un point C.

On reproduit ce programme de l'autre côté du segment de manière à reproduire un parallélogramme ACBD, avec D le croisement des deux autres demi-droites.

[AB] et [CD] sont donc des diagonales, et par définition du parallélogramme, elles se coupent en leur milieu. On a donc le milieu du segment [AB], et donc sa moitié.

Question n°2 :

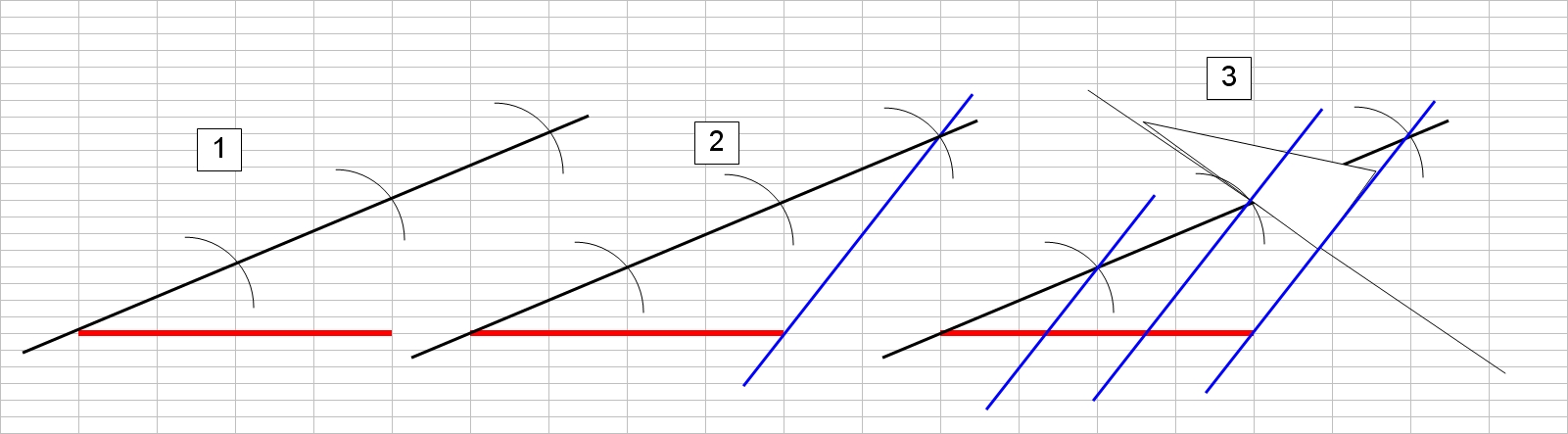
On trace un nouveau segment [IJ] et une demi-droite [Iz). Soit K un point de la demi-droite [Iz). Avec le compas, on prend la longueur IK.
On reporte la pointe sur K et on trace un cercle qui coupe [Iz) en un nouveau point (pas I ) L. On a donc IK = KL.
On reproduit cette action en plaçant la pointe du compas sur L, et on obtient un point M. On a donc IK = KL = LM.
On trace (JM) et ses parallèles qui passent par K et L, à l'aide de la règle et de l'équerre.
Notons N le point de croisement entre [IJ] et la parallèle à (JM). On a donc IN = (1/3)*IJ par le théorème de Thalès.

Voilà !

Merci pour cette énigme !

Alexein41

P.S. : J'ai droit au bonus ?

Bonjour

Pour la moitié d'un segment, je propose de construire un rectangle à l'équerre, puis tracer ses diagonales à la règle.
La perpendiculaire au segment passant par l'intersection des diagonales du rectangle ainsi construit est la médiatrice du segment.


Pour diviser un segment en 3, on applique Thalès, on trace donc au compas 3 segments égaux sur une droite passant par une extrémité du segment.
On joint le point le plus éloigné à l'autre extrémité du segment
On construit les parallèles à cette droite à la règle et à l'équerre et cela divise le segment en 3.


J'ai le bonus ?

1) Je suppose donc qu'on ne reporte aucune mesure. Voici une solution sans reporter de mesure: construire un rectangle à l'équerre et à la règle dont un coté est le segment de départ (tracer la droite support du segment, les 2 perpendiculaires la cette droite passant chacune par une extremité du segment et ensuite une parallele la la droite d'origine ou une perpendiculaire a une des 2 droites tracees).
Tracer les diagonales (regle). L'intersection des diagonales est sur la médiatrice du segment.
Projeter (orthogonalement) l'intersection des diagonales sur le segment de départ pour obtenir son milieu. Si cette méthode n'est pas assez "précise", recommencer la construction d'un second rectangle (par exemple de l'autre coté du segment) pour avoir un second point de la médiatrice et tracer la médiatrice. Son intersection avec le segment donne le milieu

2) Thales
Tracer une droite inclinée avec le segment (non confondue, non orthogonale) coupant le segment à une de ses extrémités. De préférence formant un angle aigu avec le segment du coté du segment pour plus de praticité. Reporter 3 fois la même longueur (quelconque) sur cette droite à partir de l'extrémité du segment. Joindre le dernier point porté à la deuxieme extremité du segment.
On a alors un triangle dont un coté est le segment, un deuxieme cote est DEJA divisé en 3 longueurs egales et un troisieme cote qui joint l'extremite du second cote au segment initial. En tracant les 2 // a ce troisieme cote passant par chacune des 2 marques de report de la distance choisie, chaque parallele coupe le segment initial dans le meme rapport (Thales) soit 1/3 et 2/3 de sa longueur. Bon le texte est un peu "lourd" mais un petit dessin serait plus simple mais je ne suis pas trop a l'aise avec ni faire le dessin ni le mettre en ligne.

comment résoudre l'énigme posée à un élève de 6e :
10 segments 20 points d'intersection ?
10 semi droites 20 points d'intersection ?
10 droites 20 points d'intersection ?

En fait, je crois que je n'ai même pas compris l'énoncé

bonjour  a tout le monde
  j'ai un devoir maison a rendre et ya un bonus et il disent  "comment retrouver le centre d'un cercle a l'équerre non graduée "

et aussi comment retrouver le centre d'un cercle  au compas et a la règle  non graduée !!! si vous plait  aider moi

Toujours aussi viandard, le Shadock

Pour ma part, j'aurais bien gentiment laissé de côté les fautes d'orthographe et filé un coup de main, mais j'ai toujours été pourri en géométrie

bin faut tracer deux cordes du cercle, puis leurs mediatrices se coupent en le centre. Pour la mediatrice au compas c'est facile. Avec l'equerre, utiliser la technique pour trouver le milieu plus haut et bingo !

2 tangentes et les perpendiculaires aux points de contact avec le cercle
l'intersection donne le centre

si je ne me trompe,

C'est pas un réflexe, enfin j'ai plus vraiment ce problème maintenant que j'enfonce convenablement le compas -_- (omg la discuss)