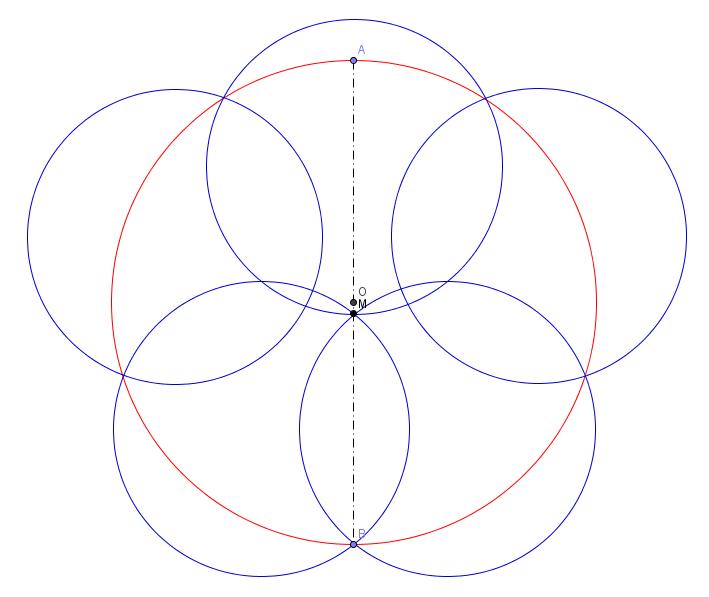
Bonjour
Merci schaff60 pour tes précisions par MP + le lien de Kosmogol.
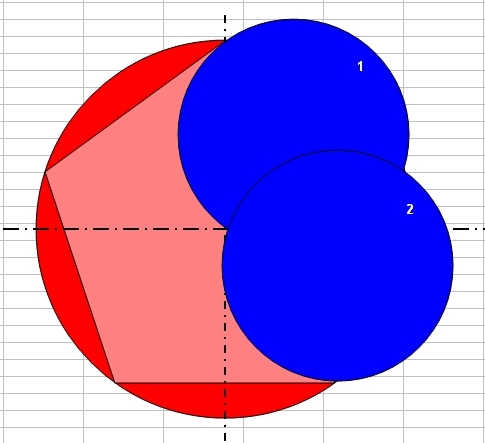
On doit placer 5 disques "bleus", donc je vais raisonner avec un pentagone inscrit dans le disque "rouge"
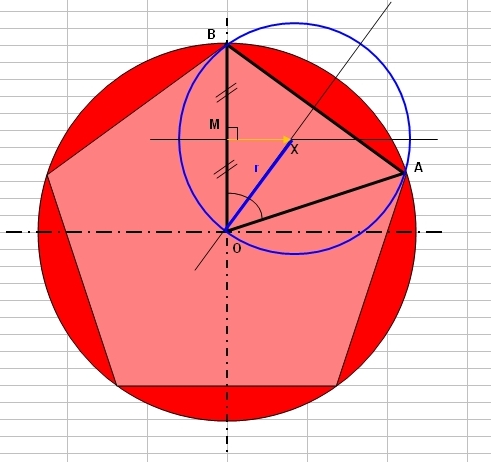
Soit un pentagone inscrit dans un cercle de rayon unitaire et de centre O
Ce pentagone décompose en 5 triangles isocèles juxtaposés de sommets O.
Soit OAB l'un de ces triangles, dont l'angle Ô vaut 72° (ou 2Pi /5)
Une première approche de solution de recouvrement du disque unitaire par 5 disques de rayon r est de centrer ce cercle en un point X situé sur la médiatrice de [AB] qui passe donc par O, la circonférence de ce disque passe par O, A et B
On a r = OX
M milieu de [OB]
OM = 1/2
on a ainsi r * cos (72°/2) = OM =1/2
i.e. r * cos (2*pi /10) = 1/2
r vaut donc [(1/2) / cos (36°)] soit 0.618
Ramené aux unités de l'énoncé, on conclut que :
5 disques bleus de 61 cm de diamètre disposés sur les 5 médiatrices ne suffisent donc pas à recouvrir le disque rouge de 1 m de diamètre
> il faudrait 61,8 cm.
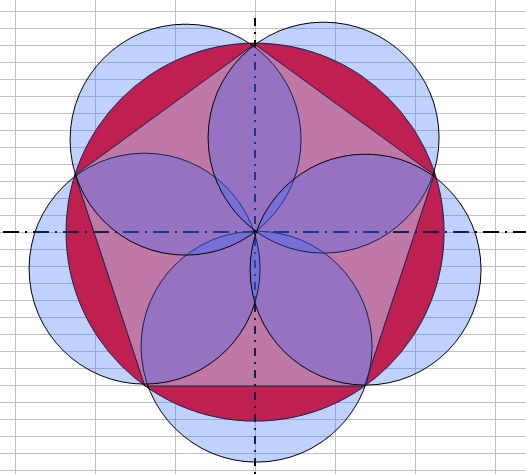
La figure ci-dessous est avec 61.8 cm :
Au passage, on a la dimension d'un côté du pentagone inscrit :
2*sin(36°) soit 1,176
> soit 58,5 cm avec les données de l'énoncé.
Si on retente avec 61.8 cm (au lieu de 61) :
Avec 61,8 cm, les 4 premières arêtes du pentagones sont "couvertes" et on remarquera néanmoins que le "4ème" disque posé et le premier disque recouvrent déjà le centre et une portion du cinquième "triangle", donc poser un 5ème disque de 61.8 cm est aisé et recouvrira sans peine la dernière portion.
On y arriverait aussi bien avec un 5ème disque de diamètre égal à un côté du pentagone inscrit soit 58.5 cm.
(merci Schaff pour le MP)
La figure ci-dessous est toujours avec 61.8 cm pour les 4 premiers disques "bleus"
Intéressant !
A bientôt

 Accueil
Accueil
 Forum
Forum