|
#1 - 06-10-2010 22:42:07
- luthin
- Professionnel de Prise2Tete
- Enigmes résolues : 36
- Messages : 124
Dénomrbement des familles d'accords
{DO-RE-MI} est un accord à trois sons de la même famille que {RE-MI-FA#} (il y a les mêmes intervalles), de même que {RE-DO-MI} ou tout autre permutation.
D'autre part, on ne peut pas doubler les sons, {DO-DO-RE}={DO-RE} est un accord à deux sons.
Je vous demande alors de me dénombrer les familles d'accords à 4 et 6 sons.
Pour les non-musiciens, je vous donne les sons possibles:
DO-DO#-RE-RE#-MI-FA-FA#-SOL-SOL#-LA-LA#-SI, que l'on peut remplacer indifféremment par 1-2-3-4-5-6-7-8-9-10-11-12. Avec cette notation, on a:
{DO-RE-MI}={1,3,5}={RE-MI-FA#}={3,5,7}.
Spoiler : Indices
#2 - 06-10-2010 22:53:47
- laura
- Professionnel de Prise2Tete
- Enigmes résolues : 49
- Messages : 252
- Lieu: Angleterre
dénombremznt des familles d'accords
Si les accords type {do-do-do-do} sont autorisés il y a 12^4 accords à 4 sons possibles (soit 20736) et 12^6 a six temps (soit 2985984).
Si tu n 'utilise qu'une fois chaque note tu en as 12*11*10*9 (= 11880) à 4 temps et 12*11*10*9*8*7 (=665280) à 6 temps.
#3 - 06-10-2010 23:06:53
- luthin
- Professionnel de Prise2Tete
- Enigmes résolues : 36
- Messages : 124
Dénombrement des famillse d'accords
J'ai oublié de préciser qu'on ne peut pas doubler un son. {DO-DO-RE}={DO-RE} est un accord à deux sons. D'autre part, je demande le nombre de familles d'accords, pas le nombre d'accords.
Par exemple, il y a 1 famille "d'accords" à 1 son, 6 familles à 2 sons...
#4 - 06-10-2010 23:08:50
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
dénombrement ded familles d'accords
C'est quand même assez compliqué , surtout si on reconnait que théoriquement Do# et Reb ne sont pas les même notes 
Vasimolo
#5 - 06-10-2010 23:16:16
- luthin
- Professionnel de Prise2Tete
- Enigmes résolues : 36
- Messages : 124
dénombrement des falilles d'accords
Ici, on se place dans le tempérament égal où DO# est strictement équivalent en terme de hauteur à REb. Ce n'est pas là le problème, Il y a douze sons que l'on note comme on veut. Oui, c'est assez difficile.
#6 - 06-10-2010 23:47:54
- MthS-MlndN
- Hors d'u-Sage
- Enigmes résolues : 49
- Messages : 12,414E+3
- Lieu: Rouen
dénombrement des damilles d'accords
On va essayer.
Une famille d'"accords à une note", puisque chaque note est équivalente aux autres "à une transposition près" (ça fait toujours aussi bizarre, en maths, d'aller tendre vers les cas limites). Une seule famille d'accords à 11 notes également, car jouer onze notes revient à en éliminer une, donc un accord à 11 notes est "un non-accord à une note", et il y a autant de familles d'"accords à une note" que de "non-accords à une note". Ce genre de "parallélisme" est un grand classique dans tout ce qui ressemble à de la combinatoire.
Pour les accords à deux notes : on choisit de partir de la note 1 (qui est équivalente à toutes les autres, voir ci-dessus). On peut lui ajouter la note 2 (accord de deux notes voisines), ou 3 (un ton d'écart), ou 4 (un ton et demi), ou 5 (deux tons), ou 6 (deux tons et demie), ou 7 (trois sons). L'accord 1-8 est équivalent à l'accord 8-1 qui est un accord à deux tons et demie tout comme 1-6, et de la même façon, 1-9 est équivalent à 1-5, 1-10 à 1-4, 1-11 à 1-3, et 1-12 à 1-2. Oh tiens, encore de jolies symétries... Vive la combinatoire sur ensemble tournant  En tout cas, ça nous fait six familles d'accords à deux notes, et donc six familles d'accords à dix notes. En tout cas, ça nous fait six familles d'accords à deux notes, et donc six familles d'accords à dix notes.
Et comme je ne trouve pas encore de règle de construction itérative, je m'assieds dessus et je tourne. A demain 
Podcasts Modern Zeuhl : http://radio-r2r.fr/?p=298
#7 - 07-10-2010 15:08:41
- luthin
- Professionnel de Prise2Tete
- Enigmes résolues : 36
- Messages : 124
Dénombrement des famillees d'accords
Mathias, pour l'instant, je suis entièrement d'accord avec toi! Tu as compris que les symétries jouent un rôle important dans ce problème Spoiler : indice , les invariances par rotation en particulier
.
J'ai ajouté des indices dans le sujet.
Bonne continuation.
#8 - 09-10-2010 08:11:13
- luthin
- Professionnel de Prise2Tete
- Enigmes résolues : 36
- Messages : 124
Dénombrement des familles d'accods
Question intermédiaire plus directe: Combien y a t-il de familles invariantes par rotation? (On peut les dénombrer "à la main" et elles se comptent sur les doigts d'une main dans les deux cas).
Après, il ne reste plus qu'à raisonner sur le nombre d'aspects...
#9 - 10-10-2010 10:06:20
- luthin
- Professionnel de Prise2Tete
- Enigmes résolues : 36
- Messages : 124
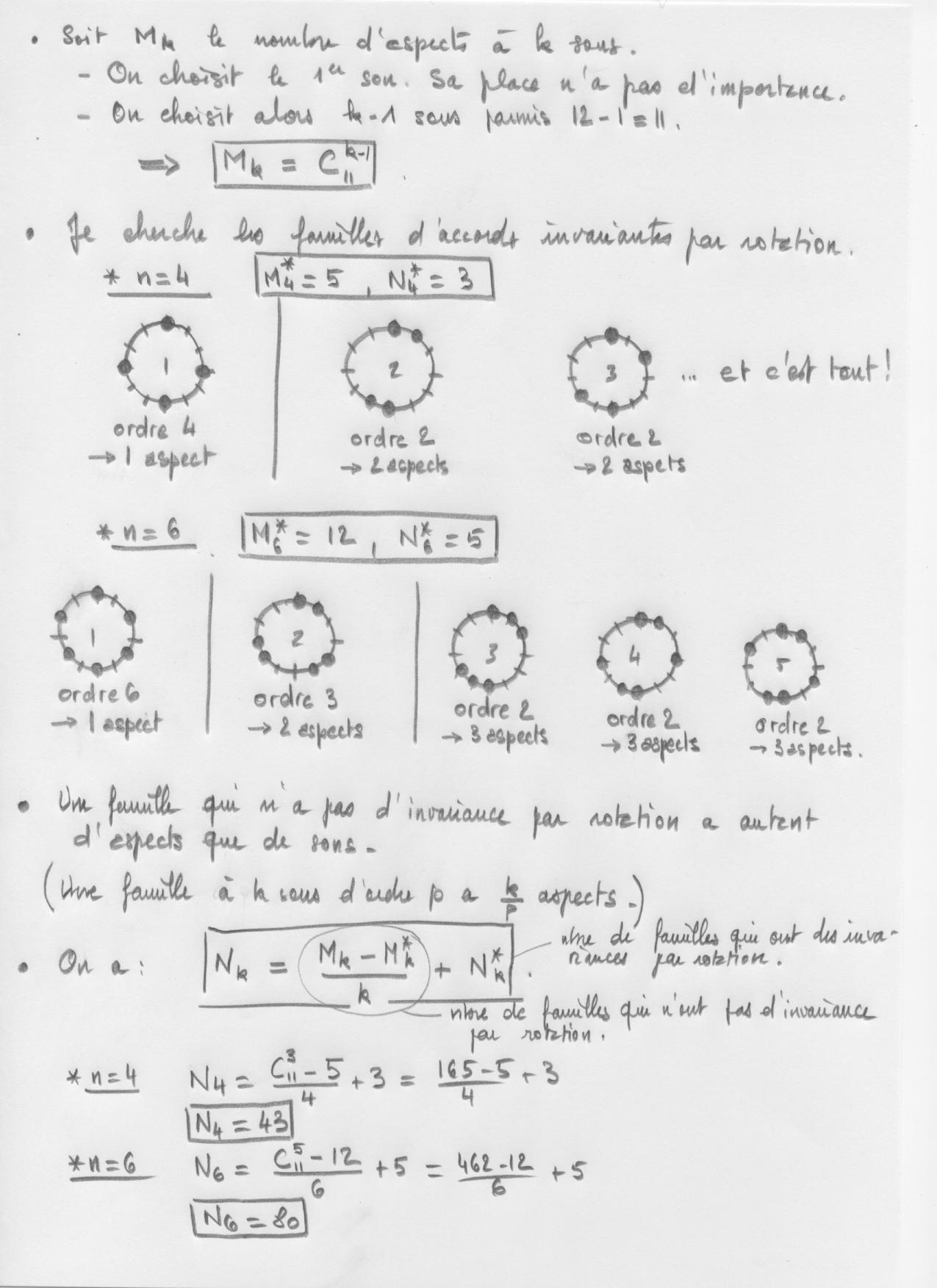
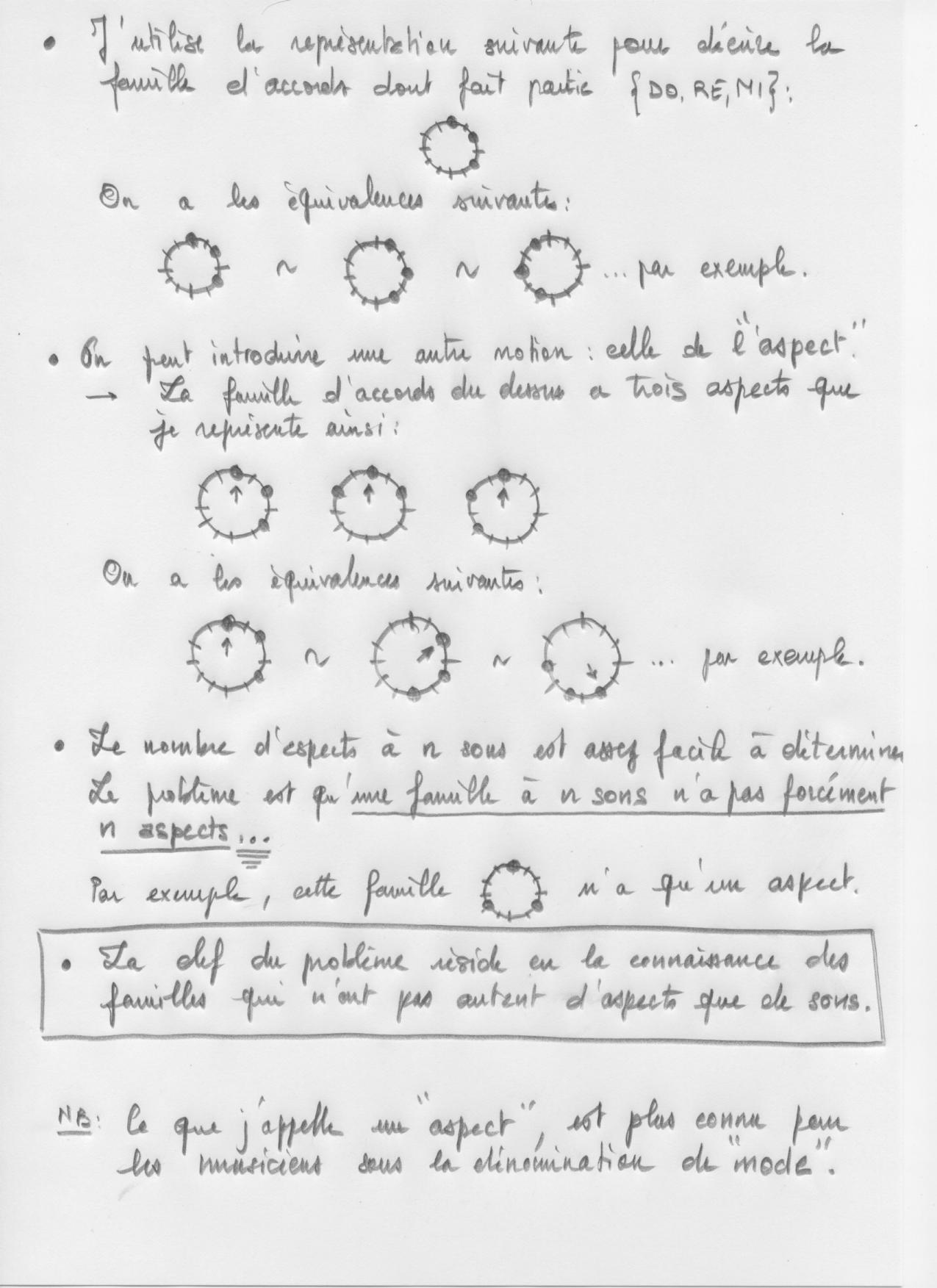
Dénombrement des famillles d'accords
#10 - 10-10-2010 10:09:37
- emmaenne
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3073
- Lieu: Au sud du Nord
dénombrzment des familles d'accords
Pour moi, c'est surtout que je n'ai rien compris du tout à la question. 
Dans le cadre de la quinzaine du beau langage, ne disez pas disez, disez dites. (Julos Beaucarne)
#11 - 10-10-2010 10:31:09
- McFlambi
- Professionnel de Prise2Tete
- Enigmes résolues : 48
- Messages : 144
dénomvrement des familles d'accords
non moi je trouve ca interessant mais long a faire et je manque de temps la
#12 - 10-10-2010 12:25:45
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Dénombremment des familles d'accords
C'est marrant , tes disques me rappellent un petit appareil que j'avais bricolé il y a quelques temps avec deux disques et qui donnait tous les accords ( 3 , 4 , 5 tons ) sans confondre les do# et les réb ni même les do* et les ré .
Par exemple Fa#7Maj=Fa#,La#Do#,Mi# .
J'étais un peu fou à l'époque 
Vasimolo
#13 - 10-10-2010 12:27:09
- MthS-MlndN
- Hors d'u-Sage
- Enigmes résolues : 49
- Messages : 12,414E+3
- Lieu: Rouen
Dénombreement des familles d'accords
Tout comme McFlambi, j'ai manqué de temps pour finir... Grâce à ton premier indice, j'aurais sans doute pu y arriver sans difficulté majeure, en plus...
Podcasts Modern Zeuhl : http://radio-r2r.fr/?p=298
#14 - 01-04-2012 23:37:55
- shadock
- Elite de Prise2Tete
- Enigmes résolues : 39
- Messages : 3334
Dénmbrement des familles d'accords
Vasimolo a écrit:C'est marrant , tes disques me rappellent un petit appareil que j'avais bricolé il y a quelques temps avec deux disques et qui donnait tous les accords ( 3 , 4 , 5 tons ) sans confondre les do# et les réb ni même les do* et les ré .
Par exemple Fa#7Maj=Fa#,La#Do#,Mi# .
J'étais un peu fou à l'époque 
Vasimolo
Je suis curieux de voir à quoi ça ressemble. Est-ce possible ? 
"L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
#15 - 01-04-2012 23:54:12
- Klimrod
- Elite de Prise2Tete
- Enigmes résolues : 40
- Messages : 4050
- Lieu: hébesphénorotonde triangulaire
Dénombrement des familles d'accord
Vasimolo a écrit:J'étais un peu fou à l'époque 
Shadock a raison : je suis curieux de voir à quoi ça ressemble. Est-ce possible ? 
J'ai tant besoin de temps pour buller qu'il n'en reste plus assez pour bosser. Qui vit sans folie n'est pas si sage qu'il croit.
#16 - 02-04-2012 00:03:19
- SHTF47
- Imprnnçbl de Prs2Tt
- Enigmes résolues : 39
- Messages : 1629
- Lieu: Autre nom du colin
Dénombrement des familles d'accordds
Ne vous attendez pas à quelque chose d'extraordinaire... A mon humble avis, c'est juste une tourtière aux pommes, avec des traits tirés à la règle un peu partout, et des notes de musique en crème patissière. 
La musique est une mathématique sonore, la mathématique une musique silencieuse. [Edouard HERRIOT]
#17 - 02-04-2012 23:06:00
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
dénombrement des familled d'accords
J'ai retrouvé ça dans un vieux carton :

les deux disques peuvent tourner autour du bouton pression . j'avais une fiche donnant les degrés composant les différents accords mais maintenant on doit trouver ça à peu près partout sur la toile .
Sur l'image le disque supérieur est positionné sur une tonique de LA et on peut lire par exemple que l'accord de La avec 7ème majeure est constitué des notes :
La , Do#,Mi,Sol# .
Je vous laisse deviner la composition du disque inférieur 
Vasimolo
#18 - 03-04-2012 03:47:28
- Moriss
- Professionnel de Prise2Tete
- Enigmes résolues : 37
- Messages : 460
énombrement des familles d'accords
Bon grosso modo :
Le cercle inférieur est divisé à peu près en 7 parts, avec à l'intersection entre 2 parts les différentes altérations d'une note (ex : do b, do, do#).
Pour construire le cercle, il faut en fait le diviser en des parts d'un peu plus de 1/7 pour inclure toutes les notes possibles. Par exemple, on peut le diviser tous les 52° (52°x7=364° au lieu de 360°).
Plus précisément, il vaut mieux faire des parts par groupe de 4 (pour s'accorder sur la quinte qui est constante quel que soit l'accord) :
fa + 208° = do ; +208°=sol ; +208°=ré ; +208°=la ; +208°=mi ; +208°=si ; +208°=fa# (eh oui, on ne retombe pas sur fa puisqu'un tour des 7 notes fait ici 364°...) et ainsi de suite.
C'est un peu long à démontrer mais ça marche  . Bien sûr, le choix de commencer par fa n'est pas hasardeux ; ceci dit, si on veut la plupart des notes usuelles, il vaut mieux commencer par fa bémol (et finir par si#). . Bien sûr, le choix de commencer par fa n'est pas hasardeux ; ceci dit, si on veut la plupart des notes usuelles, il vaut mieux commencer par fa bémol (et finir par si#).
Le disque présenté ci-dessus semble commencer par fa bb et finir par si*.
Edit : je n'ai pas trouvé ça sur la toile mais en reprenant mes vieux cours de solfège et en essayant de les appliquer à la fabrication du disque (je n'avais jamais rien vu de tel auparavant mais je trouve ça formidable !).
#19 - 03-04-2012 10:46:20
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
dénombrement des famikles d'accords
Voilà le disque inférieur .

Vasimolo
#20 - 03-04-2012 19:36:10
- shadock
- Elite de Prise2Tete
- Enigmes résolues : 39
- Messages : 3334
Dénombrement des afmilles d'accords
Merci beaucoup 
Je vais imprimer ça et essayer de comprendre comment ça marche. ^^
Parce que là tu t'es placé sur la tonique de "la" mais les autres notes elles sont où  ? ?
"L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
#21 - 03-04-2012 21:04:56
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Dénombrement des familles d'aaccords
Le disque supérieur :

Vasimolo
#22 - 03-04-2012 21:07:43
- shadock
- Elite de Prise2Tete
- Enigmes résolues : 39
- Messages : 3334
dénombrement des familles d'accordq
A oui d'accord et bien tout s'explique merci pour cette trouvaille ingénieuse même si je n'en ai pas besoin, à force de jouer ça devient une évidence.
PS : Je confire il faut être un peu fou, mais quand on s’ennuie et qu'on veut faire quelque chose d'utile...
Shadock
"L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
#23 - 03-04-2012 21:42:09
- shadock
- Elite de Prise2Tete
- Enigmes résolues : 39
- Messages : 3334
Dénombrement des familles da'ccords
Petit oubli, il manque les 11ème mais bon ce n'est qu'un détail je vais faire la version 1.1 de ta création. ^^
"L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
#24 - 03-04-2012 22:02:17
- SHTF47
- Imprnnçbl de Prs2Tt
- Enigmes résolues : 39
- Messages : 1629
- Lieu: Autre nom du colin
dénombeement des familles d'accords
En tant que guitariste, et puisqu'en ce moment je prépare des cours pour un élève, tout ça m'a donné une idée pour apprendre les accords, quelle que soit la tonalité.

Ici, c'est la représentation pour un guitariste droitier d'un accord majeur, avec la tonique en rouge, la tierce majeure en vert et la quinte en noir. L'accordage est standard, soit Mi-La-Ré-Sol-Si-Mi.
Les cercles sont en fait les cordes de la guitare, du Mi grave pour le plus petit cercle au Mi aigu pour le plus grand. Les douze segments représentent des frettes, chaque espace entre deux segments consecutifs fait donc un demi-ton.
On voit ainsi d'un seul coup d'oeil toutes les façons possibles de jouer l'accord, sachant qu'en général un accord de guitare occupe 3 ou 4 cases successives, voire 5.
Je ne sais pas si cette représentation existe déjà pour les accords (ou les gammes) de guitare, en tous cas je compte bien recenser tout ce que je peux avec. Je me demande seulement si mon élève va trouver ça pratique, et si il va progresser de manière plus efficace qu'avec des méthodes traditionnelles...
La musique est une mathématique sonore, la mathématique une musique silencieuse. [Edouard HERRIOT]
#25 - 03-04-2012 22:11:47
- shadock
- Elite de Prise2Tete
- Enigmes résolues : 39
- Messages : 3334
Dénombrrement des familles d'accords
Ca à l'air pas mal, mais je n'y connais rien en guitare et par curiosité pour rester dans la simplicité comment on lit l'accord de do majeur sur ce joli cercle ?
"L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum