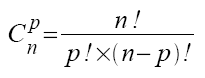Forum dédié aux énigmes et à toutes formes de jeux de logique. | Déconnexion |
|
Tu n'es pas identifié sur Prise2tete : s'identifier.  Accueil Accueil
 Forum Forum
|
 |
#1 - 25-09-2011 12:48:09
Dénombrement sur échiquirBonjour à tous.
#0 Pub#2 - 28-09-2011 11:19:03
dénombrement sur écgiquierBonjour, #3 - 28-09-2011 11:59:32
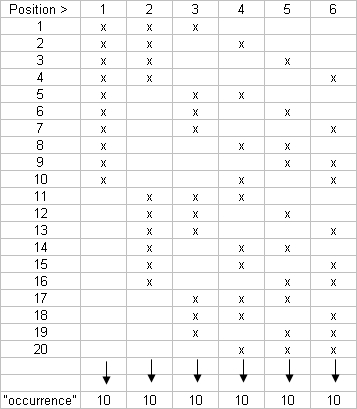
dénomnrement sur échiquierJe pense qu'il existe 20 manière de positionner les jetons sur une ligne. #4 - 28-09-2011 13:03:21
Dénnombrement sur échiquierBonjour Il aurait pu pleuvoir, con comme il est ! (Coluche) #5 - 28-09-2011 18:07:03
Dénombrement sur échiqquier@Nicko: ton tableau est bien renseigné, il permet de voir qu'il y a qq chose de pas compris, ou que j'ai mal expliqué: il faut bien 1 pion dans la colonne 1, 2 dans la colonne 2, ...et 6 dans la colonne 6, ce qui fait bien 6*7/2=21 pions en tout. Et donc comme il y a 7 lignes, il faut 3 pions par ligne. #6 - 29-09-2011 07:33:17
Dénombrement sur échiquerBonjour ! Il aurait pu pleuvoir, con comme il est ! (Coluche) #7 - 29-09-2011 13:46:21
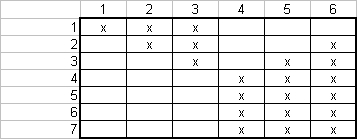
dénolbrement sur échiquierNickoGecko, je me trompe peut-etre car je n'ai pas tout compris au problème, mais je pense qu'il n'y a pas qu'un seul motif de base. #8 - 29-09-2011 14:36:10
dénombrement syr échiquierAh oui ! tu as raison ! Il aurait pu pleuvoir, con comme il est ! (Coluche) #9 - 29-09-2011 17:23:11
Dénombrement sur céhiquier
Je confirme bien cette remarque. #10 - 30-09-2011 06:54:28
Dénmbrement sur échiquierBonjour, Il aurait pu pleuvoir, con comme il est ! (Coluche) #11 - 30-09-2011 17:37:39
Dénombreent sur échiquierPour NickoGecko: Réponse rapideSujets similaires
Mots clés des moteurs de recherche |
 | |||||||||||||||||||||||||||||||||
| Prise2Tete Forum Statistiques Liste des membres Hall of Fame Contact | |||||||||||||||||||||||||||||||||||
Un jeu où seules la réflexion, la logique et la déduction permettent de trouver la solution.