 |
#1 - 21-01-2018 20:10:51
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Dénombrement ptissier
Bonjour à tous,
n'ayant pas abandonné le gâteau 149, je suis tombé sur un problème intéressant de dénombrement.
On dispose 12 pépites de chocolat sur un gâteau en forme de grille de 6x6 cases, de sorte que chaque ligne et chaque colonne contienne exactement 2 pépites.
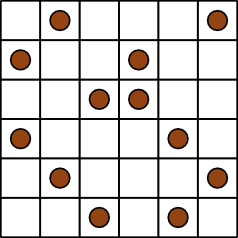
Combien y a-t-il de façons de procéder, si l'on considère que deux gâteaux symétriques sont différents ?
Je précise pour les allergiques qu'il est possible de résoudre ce problème sans ordinateur 
#2 - 22-01-2018 17:38:21
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
Dénombremnet pâtissier
67950 tombe bien !
Bon, je n'ai pas cherché à finasser, enfin si un peu au début, mais je me suis perdu.
Alors j'ai défini un nombre en commençant par le plus petit :
12 12 34 34 56 56
et en échangeant les chiffres, et en y allant toujours dans le sens croissant, avec bien entendu jamais 2 chiffres dans la même paire. En remarquant les redondances, il ne m'a fallu qu'une seule page A3 pour en venir à bout.
Mais bon, j'ai eu du bol de ne pas faire d'erreurs de calcul, ni d'en oublier !
#3 - 22-01-2018 18:43:48
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Dénombrement pâttissier
@nodgim : bravo ! Il y avait moyen de finasser, la preuve dont je dispose est nettement plus compacte, mais l'essentiel c'est d'aboutir.
#4 - 24-01-2018 17:26:47
- enigmatus
- Expert de Prise2Tete
- Enigmes résolues : 0
- Messages : 561
dénombrement pâtisqier
Bonjour,
Si on part d'une pépite, et qu'on se déplace jusqu'à la suivante alternativement horizontalement et verticalement, on finit par revenir au point de départ.
Les seuls cycles possibles ont pour longueur 4, 6, 8 ou 12.
Avec 12 pépites, on peut avoir un des 4 cas suivants :
1) 3 cycles de 4
2) 1 cycle de 4 + 1 cycle de 8
3) 2 cycles de 6
4) 1 cycle de 12
Si on appelle A(n,p) le nombre d'arrangements de n éléments pris p à p, le nombre de possibilités dans chaque configuration est :
soit un total de 67950 possibilités.
J'ai vérifié le résultat avec un script en python3 qui place les pépites dans toutes les positions possibles.
#5 - 24-01-2018 19:24:18
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Dénombreent pâtissier
Félicitations ! Très jolie méthode de dénombrement, et très efficace 
enigmatus a présenté une solution qui ne nécessite que 4 calculs pas trop compliqués.
#6 - 25-01-2018 17:41:57
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
dénombrement pâtidsier
Bonsoir Ebichu
Je n'ai pas eu beaucoup de temps libre cette semaine , si tu pouvais laisser caché jusqu'à samedi 
Vasimolo
#7 - 25-01-2018 17:52:50
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
dénombrement pâtisdier
Bien sûr, je rajoute du temps.
#8 - 26-01-2018 08:35:54
- nobodydy
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1677
#9 - 26-01-2018 19:15:45
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
dénombrement pâtissizr
@nobodydy : je n'y avais même pas pensé, bravo 
#10 - 27-01-2018 16:19:58
Dénoombrement pâtissier
Salut
Je dirais (C(6,2).C(4,2).C(2,2))^2=8100
#11 - 28-01-2018 10:00:13
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Dénombreent pâtissier
J'ai quand même fini par en venir à bout 
Je n'ai pas trouvé d'astuce combinatoire , je me suis rabattu sur les probabilités en choisissant au hasard une paire sur chaque ligne :
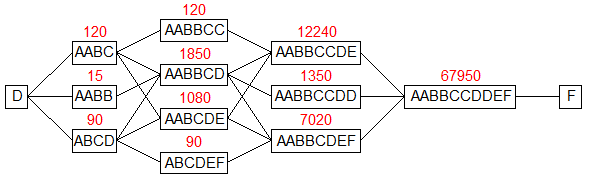
C'est "un peu" lourd , on doit pouvoir faire plus simple .
Vasimolo
#12 - 28-01-2018 11:54:43
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Dénombrement pâtissire
@Flight : salut, non, ce n'est pas ça. C'est un peu plus compliqué.
@Vasimolo : très bien ! La méthode dont je dispose est du même niveau de complexité, j'ai l'impression que c'est la méthode "duale" de la tienne. Je doute que l'on puisse faire beaucoup plus simple.
#13 - 30-01-2018 09:21:40
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
DDénombrement pâtissier
C'est terminé, merci à tous les participants.
Voici ma façon de voir les choses. On remplit les colonnes une par une, de gauche à droite, de toutes les façons possibles.
Pour la première colonne, il y a [latex]\binom{6}{2}=15[/latex] façons de procéder. Puis il faut maintenant remplir 5 colonnes, de sorte que 2 des lignes contiennent 1 pépite, et 4 des lignes contiennent 2 pépites. Pour remplir la 2e colonne, il faut donc distinguer 3 cas :
* les 2 pépites de la colonne tombent chacune sur une des 2 lignes où 1 pépite manque (1 façon de procéder).
* les 2 pépites de la colonne tombent l'une sur une des 2 lignes où 1 pépite manque, l'autre sur une des 4 lignes où 2 pépites manque (2*4=8 façons de procéder).
* les 2 pépites de la colonne tombent chacune sur une des 4 lignes où 2 pépites manque ([latex]\binom{4}{2}=6[/latex] façons de procéder).
Il faut ensuite continuer récursivement le procéder. Pour généraliser, appelons [a,b] le nombre de façons de remplir un rectangle où a représente le nombre de lignes où 1 pépite manque, et b le nombre de lignes où 2 pépites manquent.
Le nombre de lignes du rectangles est alors (a+b), tandis qu'il comporte (a+2b)/2 colonnes.
Le raisonnement ci-dessus se généralise par la relation [latex][a,b]=\binom{a}{2}[a-2,b]+\binom{a}{1}\binom{b}{1}[a,b-1]+\binom{b}{2}[a+2,b-2][/latex], soit [latex][a,b]=a(a-1)/2[a-2,b]+ab[a,b-1]+b(b-1)/2[a+2,b-2][/latex].
On recherche dans ce problème la valeur de [0,6], et on peut l'obtenir à l'aide du tableau suivant.
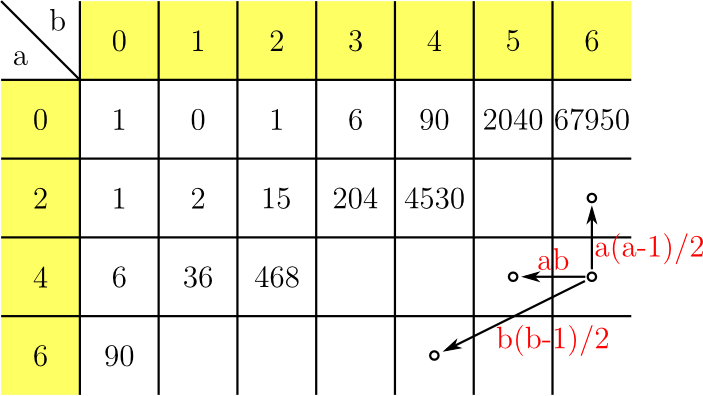
On initialise [0,0] à 1, puis on remplit le tableau de haut en bas, puis de gauche à droite. En bas à droite, j'ai indiqué comment remplir une case à partir de 3 cases précédentes (ou moins si on est près du bord du tableau). Par exemple, pour la case [2,4], on fait 2(2-1)/2[0,4]+2*4[2,3]+4(4-1)/2[4,2]=1*90+8*204+6*468=4530.
La solution était donc 67950, bravo à ceux qui ont trouvé. Comme observé par nobodydy, OEIS connaissait...
En question bonus, en généralisant ce raisonnement, j'arrive à calculer le nombre de façons de remplir une grille 9x9 de sorte que chaque ligne et chaque colonne contienne exactement 3 pépites, mais comme cela représente plusieurs dizaines de calculs, j'ai eu recours à un programme. On doit trouver un nombre à 14 chiffres ne comportant ni 3 ni 4, et OEIS le connaît.
|
 |

 Accueil
Accueil
 Forum
Forum









