 |
#1 - 11-10-2010 17:11:19
- Promath-
- Elite de Prise2Tete
- Enigmes résolues : 18
- Messages : 1416
- Lieu: Au fond de l'univers
les tauprs
J'ai adorééééééé ce problème, issu du championnant des jeux mathematiques2005
18 - LA TAUPINIÈRE (coefficient 18)
Cinq trous de taupe, assimilés à des points, se trouvent à l’intérieur,
bord compris, d’un carré de pelouse dont le côté mesure
12 mètres de longueur. Trois trous quelconques ne sont jamais
alignés.
Au maximum, quelle est la plus petite surface de tous les triangles
formés par trois trous ?
Vous donnerez la réponse exacte en m2, même si elle est irationnelle.
Un promath- actif dans un forum actif
#2 - 11-10-2010 17:35:21
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Les taueps
C'est sûrement 36cm² mais il faudrait vérifier 
Vasimolo
#3 - 11-10-2010 23:01:45
- luthin
- Professionnel de Prise2Tete
- Enigmes résolues : 36
- Messages : 124
Les tuapes
Je ne comprends pas la question.
On a 5 points, avec lesquels on peut former 10 triangles. La surface dont tu parles est-elle la somme des surfaces des 10 triangles?
Je ne comprends pas ce que veut dire "au maximum, quelle est la plus petite ..."!
#4 - 16-10-2010 19:42:30
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Les taupe
Si je peux me permettre une petite remarque 
Ce sujet comme plusieurs autres est clos depuis un moment sans aucune réaction de la part de l'auteur .
Ouvrir une énigme exige un minimum de service après-vente 
Vasimolo
#5 - 16-10-2010 19:45:49
- emmaenne
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3073
- Lieu: Au sud du Nord
les taypes
A force de se disperser on se perd.
Dans le cadre de la quinzaine du beau langage, ne disez pas disez, disez dites. (Julos Beaucarne)
#6 - 16-10-2010 19:53:17
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Les taupe
Surtout quand on ne voit quasiment rien dans ses galeries sombres ...
Ca me rappelle une chanson de Maurane 
Vasimolo
#7 - 16-10-2010 21:49:50
- rivas
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1106
- Lieu: Jacou
Les tupes
Vasimolo a écrit:Ouvrir une énigme exige un minimum de service après-vente 
Vasimolo
Je plussoie.
luthin a écrit:Je ne comprends pas ce que veut dire "au maximum, quelle est la plus petite ..."!
Voici ce que j'en comprends (mais je n'ai pas trop le temps de chercher la solution):
Pour chaque configuration des 5 trous, un des triangles à la surface la plus petite entre tous les triangles de cette configuration. On cherche la configuration telle que cette plus petite surface au sein de cette configuration soit la plus grande d'entre toutes les configurations.
Bon pas simple à expliquer clairement. J'espère que je n'ai pas embrouillé les choses...
#8 - 16-10-2010 22:34:38
- dhrm77
- L'exilé
- Enigmes résolues : 49
- Messages : 3004
- Lieu: Fanning Island-?-Lac Tele,Mali
Les atupes
Merci a Rivas pour les précisions.
Ce probleme est similaire a l'Entassement maximal de sphères dans un cube, sauf que c'est en 2 dimensions, et que l'on s'interresse aux triangles tormés par les points au lieu des distances entre les points.
La restriction que "Trois trous quelconques ne sont jamais alignés." élimie la solution de Vasimolo ou apparement il place 4 points sur les 4 coins du carré et un point au centre.
Donc, il est clair que les 5 points vont etre placés en "étoile a cinq branches" autour du carré par 3 points consecutifs (A, B, C par exemple) ils ont une petite aire., avec au moins 1 axe de symmetrie.
Si on nomme les points A, B, C, D, E dans le sens des aiguille d'une montre autour du carré.
Il est probable que les 10 triangles soient de 2 type:
- formés par 3 points consecutifs (A, B, C par exemple) ils ont une petite aire.
- formés par 3 points non-consecutifs (A, B, E par exemple) ils ont une aire plus grande.
On a ensuite 2 choix:
- une disposition ou un sommet de l'etoile sur trouve sur un coin du carré
- ou une disposition ou un sommet de l'etoile sur trouve au milieu d'un segment du carré.
ensuite pour chaque disposition, il suffit de calculer les segments pour que les petites aires soient egales, et garder la disposition qui donne la plus gande aire...
A suivre...
Great minds discuss ideas; Average minds discuss events; Small minds discuss people. -Eleanor Roosevelt
#9 - 16-10-2010 23:25:18
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
lzs taupes
Mon cher Dan:)
C'est bien comme ça que j'avais vu le problème et la solution que je proposais est "limite" dans le sens qu'on ne peut pas l'atteindre ni la dépasser mais on peut l'approcher d'aussi près que l'on veut . N'est-ce pas le maximum attendu ?
Vasimolo
#10 - 16-10-2010 23:41:18
- dhrm77
- L'exilé
- Enigmes résolues : 49
- Messages : 3004
- Lieu: Fanning Island-?-Lac Tele,Mali
Les aupes
Ha, oui effectivement, je ne l'avais pas vu comme ca.
Mais je dirais que ta solution est donc 36 - 1/∞ 
Mais, enfin la notion de non-alignement est poussé a ses limites... dans mes solutions, qui certes apparement donneront des aires plus petites, aucun groupe de 3 points ne sera VISIBLEMENT aligné..
Je pense que le probleme demanderais a etre clarifié.
Great minds discuss ideas; Average minds discuss events; Small minds discuss people. -Eleanor Roosevelt
#11 - 17-10-2010 00:57:02
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Les taues
En fait le problème n'est pas si simple et Dan avait raison , décaler le point central fait apparaître des petits triangles et le max du min n'est évident .
Vasimolo
#12 - 17-10-2010 04:46:06
- dhrm77
- L'exilé
- Enigmes résolues : 49
- Messages : 3004
- Lieu: Fanning Island-?-Lac Tele,Mali
Les taupse
Tiens, le fait de mettre le 5eme point pres du centre nous donne 8 triangles visibles. Il manque donc 2 triangles plats qui sont en fait tres petits. Ca m'avais échappé.
On en revient donc a une de mes solutions:
Pour la 2eme disposition (un sommet de l'etoile sur trouve au milieu d'un segment du carré),
je trouve une aire de 12*12*(2-sqrt(3))/2 = 19.292341855
Pour la 1ere disposition (un sommet de l'etoile sur trouve sur un coin du carré), je trouve une aire pour 5 des triangles de 12×12×((√5−1)÷2)²÷2 = 27.50155281
les autres 5 triangles on une aire de 44.49844719
Y a-t-il mieux?
Great minds discuss ideas; Average minds discuss events; Small minds discuss people. -Eleanor Roosevelt
#13 - 17-10-2010 12:45:24
- luthin
- Professionnel de Prise2Tete
- Enigmes résolues : 36
- Messages : 124
les taupeq
Ca y est, j'ai compris le principe, merci Rivas. 
Intuitivement, je placerai les points aux sommets d'un pentagone régulier.
Ma meilleure configuration est alors la suivante:
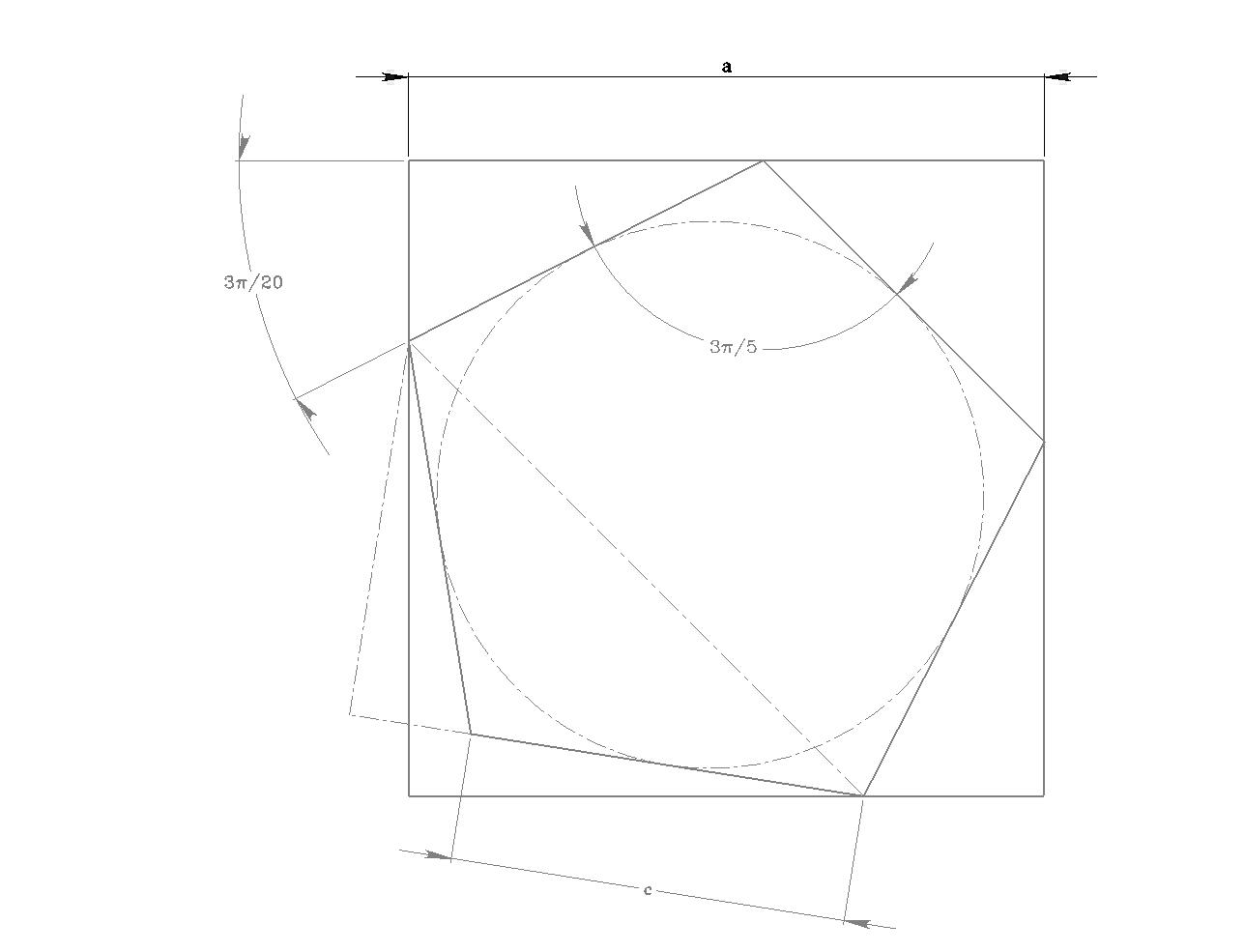
Pour le coté du pentagone, je trouve:
[TeX]c=\frac{a}{\frac 1 \sqrt 2 +\cos \frac{3\pi}{20}}[/TeX]
La plus petite aire des triangles est alors:
[TeX]\mathcal A =\frac 1 2 c^2\sin\frac{2\pi}{5}[/TeX]
Ce qui donne pour [latex]a=12[/latex]:
[TeX]\mathcal A \approx 26,812[/TeX]
Sinon, dhrm77, je ne comprends pas comment tu peux mettre un sommet de ton étoile (qui a l'air "régulière", puisque tu parles de deux types de triangle) dans un coin du carré...
#14 - 17-10-2010 14:33:13
- luthin
- Professionnel de Prise2Tete
- Enigmes résolues : 36
- Messages : 124
les taupeq
dhrm, je pense avoir compris...
Il est effectivement impossible de faire coïncider un sommet du pentagone régulier avec un sommet du carré, mais on peut mettre un sommet du pentagone dans un coin (c'est assez vague mais possible), ce que j'ai fait, d'ailleurs. Du coup, il y a une (ou deux) erreurs de calcul quelque part (puisqu'on ne trouve pas le même résultat... 
#15 - 17-10-2010 16:57:48
- dhrm77
- L'exilé
- Enigmes résolues : 49
- Messages : 3004
- Lieu: Fanning Island-?-Lac Tele,Mali
les yaupes
Non, je place effectivement un sommet dans le coin du carré, et le pentagone n'est pas régulier. Il a effectivement un angle droit. Mais il est symmétrique par la diagonale qui passe par ce coin.
Je fais mes calculs de maniere à ce que les triangles formés par 3 points consecutifs aient la meme aire.
Comme ceci:
 La distance du coin au trou suivant est 12 * (√5−1)÷2 = 7.416407865m La distance du coin au trou suivant est 12 * (√5−1)÷2 = 7.416407865m
Precisions:
Je parle de 2 types de triangles, non pas par forme, mais par surface.
Numerotons les sommets A, B, C, D, E en commencant par l'angle droit.
les "petits" triangles (ABC, BCD, CDE, DEA et EAB) ont tous une aire de 144×((√5−1)÷2)^2÷2 = 27.50155281000757092926974
les grands triangles (ABD, BCE, CDA, DEB et EAC) ont tous une aire de 144×((√5−1)÷2)÷2 = 44.49844719
PS: veuillez excuser les dimensions sur le dessin, elles sont en decimetres....
Great minds discuss ideas; Average minds discuss events; Small minds discuss people. -Eleanor Roosevelt
#16 - 18-10-2010 19:34:33
- luthin
- Professionnel de Prise2Tete
- Enigmes résolues : 36
- Messages : 124
Les taues
Je pense avoir trouvé une meilleure configuration.
Je fais les hypothèses suivantes:
- un point coïncide avec un sommet du carré.
- un point sur chaque coté du carré.
- la configuration est symétrique par rapport à la diagonale du carré qui passe par le premier point.
Voici la disposition:
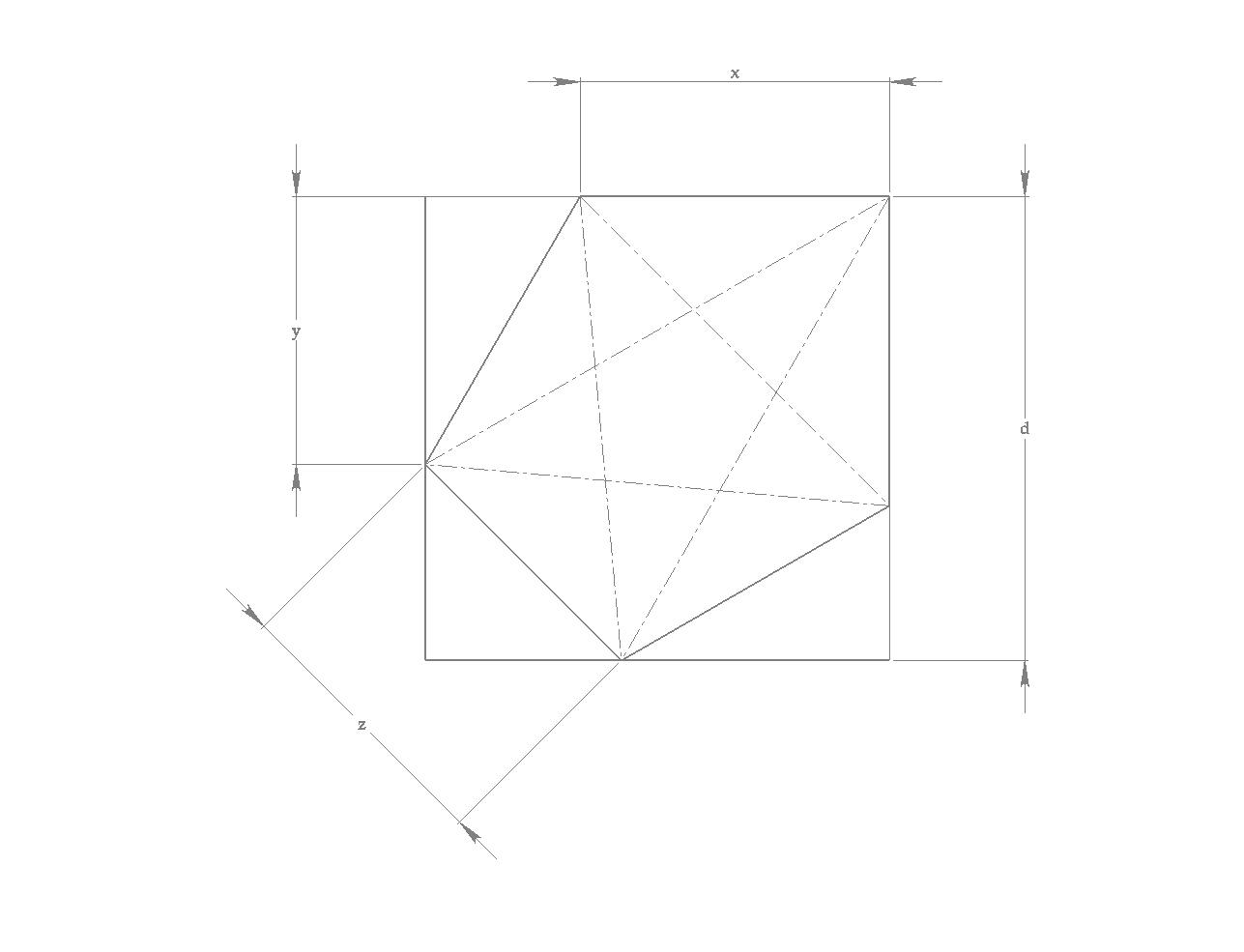
La configuration est entièrement déterminée par les deux cotes [latex]x[/latex] et [latex]y[/latex].
On a alors six aires différentes pour les triangles, qui sont:
[TeX]
\mathcal A_1=\frac 1 2 x^2
\mathcal A_2=\frac 1 2 xy
\mathcal A_3=\frac 1 2 (d-y)(d-x+y)
\mathcal A_4=\frac 1 2 xd
\mathcal A_5=\frac 1 2 x(d-x+y)
\mathcal A_6=\frac 1 2(d^2-y^2)
[/TeX]
On peut alors constater que [latex]\mathcal A_4[/latex], [latex]\mathcal A_5[/latex] et [latex]\mathcal A_6[/latex] ne sont jamais les plus petites.
Supposons [latex]y\le x[/latex]. Cela exclu [latex]\mathcal A_1[/latex] pour être l'aire la plus petite.
Dans ce cas, (...), la plus petite aire est maximum lorsque [latex]\mathcal A_2=\mathcal A_3[/latex]. Ceci implique que:
[TeX]x=d-\frac{y^2}d[/TeX]
L'aire minimale s'exprime alors sous la forme:
[TeX] \mathcal {A_{min}=\frac 1 2 (d-\frac{y^2}d)y[/TeX]
On trouve alors qu'elle passe par un maximum pour:
[TeX]\fbox{y=\frac d{\sqrt{3}}\quad \Leftrightarrow x=\frac 2 3 d}[/TeX]
Sa valeur est alors (pour [latex]d=12[/latex]):
[TeX]\fbox{\mathcal A_{min/max}=\frac{d^2}{3\sqrt 3 } \approx 27,713}[/TeX]
Pour le cas [latex]x\le y[/latex], (...), on retrouve la solution de dhrm qui est légèrement moins bonne.
#17 - 18-10-2010 23:14:00
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Les tauppes
@luthin
J'avais envisagé la même configuration que toi ( le pentagone régulier me semblait un peu léger ) mais je n'avais pas fini les calculs .
Bravo pour ton développement , si on peut faire mieux ça ne doit pas être énorme 
Vasimolo
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum








