 |
#1 - 19-02-2011 12:53:31
- halloduda
- Professionnel de Prise2Tete
- Enigmes résolues : 24
- Messages : 495
- Lieu: Ardèche
eLs 4 taupes
4 taupes vivent aux sommets d'un tétraèdre régulier dont les arêtes ont pour longueur 1.
Elles voudraient pouvoir toutes se rencontrer, elles décident donc de creuser des galeries.
Mais bien sûr, afin d'économiser leur effort, elles veulent creuser la plus petite longueur possible.
Quelle est cette plus petite longueur ? (Donner la formule exacte).
Spoiler : [Afficher le message]
La formule exacte étant difficile à entrer de façon unique dans la case de vérification,
la case n'accepte que la valeur numérique, avec un point décimal, (pas une virgule)
et trois décimales, dont la dernière est un arrondi.
Spoiler : [Afficher le message]
Même problème plus connu : relier au plus court les 4 sommets d'un carré de côté 1.
La réponse n'est pas 2√2.
Spoiler : [Afficher le message] arbre de Steiner
#2 - 19-02-2011 13:37:51
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,039E+3
Lees 4 taupes
La distance à l'orthocentre du tétraèdre.
Racine ( 3/4 - 1/12 ) * 3/4 = 0,612 pour chaque taupe.
4 taupes donc 2,449
#3 - 19-02-2011 13:53:58
- halloduda
- Professionnel de Prise2Tete
- Enigmes résolues : 24
- Messages : 495
- Lieu: Ardèche
eLs 4 taupes
Non, gwen27, les galeries doivent les relier toutes les quatre.
On demande la longueur optimisée de l'ensemble des galeries.
Qu'elles ne creusent pas 4 tunnels pour s'évader comme les Dalton.
Avec un point décimal pour la case de vérification.
#4 - 19-02-2011 13:58:20
- MthS-MlndN
- Hors d'u-Sage
- Enigmes résolues : 49
- Messages : 12,414E+3
- Lieu: Rouen
les 4 yaupes
http://fr.wikipedia.org/wiki/T%C3%A9tra%C3%A8dre
Les taupes se rejoindront au centre du tétraèdre, situé à un quart de la hauteur. Chacune aura donc parcouru trois quarts de la hauteur, et cette hauteur vaut √23 ; par conséquent, la distance parcourue est 34√23=√64 soit environ 0,612.
Si on compte les quatre galeries ensemble, on obtient une longueur globale de \sqrt 6 qu'on peut arrondir à 2,449 (la case réponse ne valide aucune des deux, même avec des points à la place des virgules... me suis-je trompé quelque part ? il ne me semble pas o_0')
Podcasts Modern Zeuhl : http://radio-r2r.fr/?p=298
#5 - 19-02-2011 14:41:56
- L00ping007
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 2010
- Lieu: Paris
led 4 taupes
En considérant que le point de rencontre est le centre de gravité du tétraèdre, la distance parcourue est 4 fois la distance d'un sommet au centre, c'est-à-dire :
d=4.(34√23)≈2.449
Non validé par la case réponse ...
#6 - 19-02-2011 15:26:24
- halloduda
- Professionnel de Prise2Tete
- Enigmes résolues : 24
- Messages : 495
- Lieu: Ardèche
les 4 raupes
Déjà 3 réponses équivalentes tombées dans le même piège.
Pourquoi aurais-je posé ce problème s'il était aussi banal ?
La case de vérification est juste.
#7 - 19-02-2011 15:34:56
- MthS-MlndN
- Hors d'u-Sage
- Enigmes résolues : 49
- Messages : 12,414E+3
- Lieu: Rouen
Les 4 taaupes
halloduda a écrit:Pourquoi aurais-je posé ce problème s'il était aussi banal ?
Eh, oh, sur un autre ton, mon p'tit bonhomme 
D'accord, mon cher, eh bien nous allons y réfléchir derechef, et avec le sourire 
Podcasts Modern Zeuhl : http://radio-r2r.fr/?p=298
#8 - 19-02-2011 15:50:44
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,039E+3
Les 4 taueps
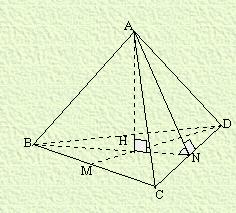
AN^2 - HN^2 = AH^2
AH= racine ( 3/4 - 3/12)
Le baricentre est aux 3/4 de cette distance, donc 3 fois la distance pour 4 taupes.
La distance est donc de : racine ( 8 / 12 ) * 3 = 2,4494897....
donc 2.449 Mais Non validé.
Conclusion : Soit je ne sais pas compter, soit ce n'est pas le barycentre.
#9 - 19-02-2011 21:02:22
- franck9525
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1935
- Lieu: 86310
Les 4 tauupes
J'aurais bien choisi le point point équidistant des sommets comme etant le point de minimal distance car il est le centre de symetrie et à la verticale du point de Fermat. Ce point se trouve au quart de la hauteur et a √6/4 d'un sommet ce qui fait une distance totale a creuser pour nos amies les taupes de √6.
Je suppose que suis tombé dans le même piège que les autres, au moins je ne serais pas tout seul 
The proof of the pudding is in the eating.
#10 - 20-02-2011 02:41:59
- mitsuidewi
- Professionnel de Prise2Tete
- Enigmes résolues : 49
- Messages : 250
- Lieu: dans une chambre universitaire
Les 4 atupes
La réponse est sur google en tapant "tétraèdre", mais je vais quand même faire les calculs.
Les 4 chemins doivent se rencontrer au centre de gravité du tétraèdre, qui représente le chemin le plus court. voici la position de ce point :

Pour calculer la position de ce point, il faut passer par le barycentre d'un des triangles, puis remonter jusqu'au point H :
Soit M, le barycentre du triangle :
Calcul de FC :
FC=CDcos(π6)=asqrt32
Car dans un triangle équilatérale, les angles font chacun 60°...
Calcul de CM:
D'après la relation de Chasles on a :
→EM+→CM+→DM=→0→EC+→CM+→CM+→DC+→CM=→02→FC−3→CM=→0→CM=−23→FC⇒CM=a√33
Calcul de AM :
D'après Pythagore :
AM2=a2−CM2AM2=2a23⇒AM=a√23
Maintenant pour trouver le point G, on réfléchit en terme de volume. On sait que le volume EDGC est le quart du volume AEDC :
13ED×CF2×MG=112ED×CF2×AMMG6=AM24MG=AM4=a4√23
Comme a=1 ,on a approximativement MG = 0.204
#11 - 20-02-2011 02:47:47
- mitsuidewi
- Professionnel de Prise2Tete
- Enigmes résolues : 49
- Messages : 250
- Lieu: dans une chambre universitaire
Les 4 taueps
Je me suis rendu compte que mon erreur est de considérer le centre de gravité comme le point de rencontre le plus rapide.
Docn si j'ai bien compris, une taupe peut très bien creuser un tunnel plus petit que les autres ? le but étant de trouver le "point de rencontre tel que la somme des 4 chemins soit la plus petite possible ?"
Si c'est juste, je pense que tu devrais modifier ton poste afin d'améliorer la compréhension.
#12 - 20-02-2011 10:52:29
- L00ping007
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 2010
- Lieu: Paris
Les 4 tuapes
J'ai trouvé l'astuce  Ce que l'on cherche n'est pas la distance parcourue par les taupes, qui est bien au minimum √6, mais la longueur creusée ! Ce que l'on cherche n'est pas la distance parcourue par les taupes, qui est bien au minimum √6, mais la longueur creusée !
La réponse est : √3+√22
EDIT
Donc, un peu de temps pour écrire ma démo.
Par contre j'ai pas encore vraiment réfléchi au problème de montrer qu'il était impossible de faire moins, mais je m'y penche 
L'idée c'est de faire se rejoindre les taupes 2 à 2 avant le centre, histoire qu'à 2 elles empruntent la même galerie. Non seulement elles font pas la fin du trajet toutes seules, mais en plus au final elles creuseront moins ... à condition de trouver la bonne configuration !
Après quelques tâtonnements :
- A et B se rejoignent au milieu de [AB], puis ensemble vont au centre. Et idem pour C et D. Mais la longueur des galeries est encore trop longue.
- A,B et C se rejoignent au centre de gravité du triangle ABC, et rejoignent D au centre : idem trop long.
En notant O le centre du tétraèdre, l'idée est de faire se déplacer A et B dans le plan (OAB). Pour des raisons de symétrie, le mieux est qu'ils se rejoignent sur la médiatrice de (AB) qui passe par O. Ce sera la même chose pour C et D, avec les mêmes distances, donc je ne traite que le cas A et B.
J'ai utilisé un repère de centre A, (AB) axes des x, et axe des y dans le plan (ABC) (D est ainsi le sommet du tétraèdre)
Les coordonnées des points A,B,C,O et I (milieu de AB) sont donc :
A(0,0,0)B(1,0,0)C(12,√32,0)I(12,0,0)O(12,12√3,12√6)
(calculs assez faciles à faire en remarquant que D est à la verticale du centre de gravité de ABC)
Je peux ainsi caculer la distance OI :
OI=√112+124OI=12√2
Il ne reste plus qu'à trouver un point M, sur (OI), tel que la distance : AM + BM + MO soit minimale. Comme AM=BM, on veut que d=2AM+MO soit minimale.
Je me place maintenant dans le triangle ABO, et je note x la distance IM
Avec un peu de Pythagore :
d(x)=2√14+x2+12√2−xd(x)=√4x2+1+12√2−x
On dérive par rapport à x :
d′(x)=4x√4x2+1−1
Cette dérivée s'annule pour : x0=12√3 (on doit pouvoir montrer proprement que c'est bien un minimum)
d(x0)=2√3+12√2−12√3d(x0)=√32+12√2
On fait la même chose pour C et D, et on trouve la même valeur. Donc on double la distance qu'on vient de trouver pour avoir la longueur totale des galeries :
L=√3+1√2
Y a besoin de montrer que cette longueur est la plus petite qu'on puisse trouver ?
#13 - 20-02-2011 11:28:56
- halloduda
- Professionnel de Prise2Tete
- Enigmes résolues : 24
- Messages : 495
- Lieu: Ardèche
Les 4 aupes
Bravo L00ping007, tu es le premier.
#14 - 20-02-2011 11:46:32
- gabrielduflot
- Expert de Prise2Tete
- Enigmes résolues : 34
- Messages : 609
Lse 4 taupes
le chemin le plus court le trouve au centre de la sphere circonconscrite au tetraedre.
ABCD le tetraedre
G le centre de gravité de la face ABC alors si H est le pied de la hauteur de A alors AH=√32 d'après le théorème de Pythagore
donc AG=23AH=√33
Soit O le centre de la sphere circonscrite alors DO=34DG car O est la barycentre (A;1)(B;1)(C;1)(D;1) et G barycentre de (A;1)(B;1)(C;1) d'où O barycentre (G;3)(D;1)
le triangle ADG est rectangle en G d'où DG²=1-13=23 d'après le théorème de Pythagore donc DG=√23 donc DO=34×√23=√38
#15 - 20-02-2011 23:59:01
- gasole
- Elite de Prise2Tete
- Enigmes résolues : 40
- Messages : 1117
- Lieu: Toulouse
eLs 4 taupes
Après avoir réfléchi un peu, j'ai entrepris des recherches... Je vais tâcher d'utiliser le moins de formules possibles.
Pour un triangle équilatéral (=donnée de 3 points), si l'on conserve 2 arêtes du triangle, la distance sera de 2. La solution optimale est connue, il faut ajouter un point (au centre du triangle) qui rejoint chacun des sommets pour une distance totale de 3^(1/2).

Ce point qu'on ajoute s'appelle un point de Steiner, c'est un point de jonction autre qu'un des points donnés initialement.
Pour le carré, la solution optimale consiste à ajouter 2 points de Steiner.

En dimension 2, un point de Steiner PS est toujours relié à exactement 3 autres points A1,A2,A3, et les angles (Ai,PS,Aj) sont tous égaux à 2π3=120∘ (sinon on peut faire mieux).
En dimension 3, je n'ai pas trouvé grand chose...
Il s'agit ici de déterminer un arbre de Steiner pour un tétraèdre régulier (cf. http://fr.wikipedia.org/wiki/Arbre_de_Steiner ).
On appelle degré d'un sommet le nombre de sommets auxquels il est relié.
Un PS a un degré au moins égal à 3 (sinon il est inutile).
Le problème est de déterminer le nombre de points de Steiner noté p qu'il faut ajouter... Il en faut au moins un dans la mesure où, tracer directement les galeries entre sommets, et donc passer uniquement par les arêtes du tétraèdre, donne une distance totale de 3 pour relier tous les sommets, alors qu'ajouter le point de Steiner pour la base du tétraèdre puis relier ce point au sommet est moins couteux.
Cas p=1
La première idée (très symétrique) est d'ajouter un PS au milieu du tétraèdre, et en effet, avec un seul PS c'est le mieux qu'on puisse faire. Pas besoin de calculs, on s'en sort avec une "démonstration" mécanique  . .
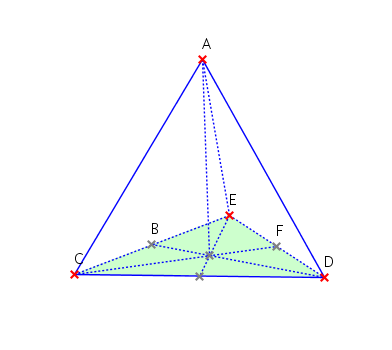
Soit M ce PS (voir figure), fixons les distances DM et AM (imaginons que les segments DM et AM soient des barres de fer librement articulées en D, en M et en A), les positions possibles du point M sont représentées par l'ellipse du diagramme.

Le long de cette ellipse, AM+DM est fixe, et seuls varient CM et BM. Il est évident que CM+BM est minimal quand CM=BM (Pour s'en convaincre, imaginons une corde fixée en A, passant dans un anneau en M, et on tire dessus depuis B pour la raccourcir, M se fixera naturellement au point de l'ellipse à égale distance de C et B). On a aussi CF=BF, mais c'est clairement moins bon.
On peut réitérer le processus sur tous les couples de sommets, et on en conclut donc que M est à égale distance des 4 points, soit au milieu du tétraèdre, à distance √38 de chaque sommet pour un total de √6∼2.4495.
Cas p=2
Voyons ce qu'on peut faire avec 2 PS M1 et M2. On a nécessairement deux sommets initiaux (disons A et B) reliés à M1, et les deux autres à M2.

Pour les mêmes raisons que dans le cas p=1, M1 doit être à égale distance de A et de B, et M2 de C et de D.
On peut imaginer que l'angle (A,M,D) est articulé en M1, et (B,M2,C) en M2, la distance totale ne change pas lorsque les angles tournent autour des PS. Faisons les tourner jusqu'à ce que A,B,M1,C,D,M2 soient coplanaires.
En ce cas, on sait que les angles autour de M1 et de M2 sont de 2π3, on en tire la distance entre chacun des sommets et le PS auquel il est relié : 12sinπ3=√33. Reste à calculer la distance séparant M1 de M2. Soient X le milieu de AB et Y le milieu de CD, X,M1,M2 et Y sont alignés pour les raisons mécaniques évoquées plus haut. Or on a d(X,M1)=d(Y,M2)=√d(A,M1)2−d(A,X)2=√1/3−1/4=1√12.
Il suffit de calculer d(X,Y) en appliquant Pythagore on trouve : d(X,Y)=√22.
D'où un total de 4.d(A,M1)+(d(X,Y)−2d(X,M1))=√3+√22∼2.439 ce qui est effectivement mieux qu'avec un seul PS.
Reste à examiner p>2.... aïe aïe aïe
Supposons qu'on ait M1, M2, M3,...,Mk, et disons que M1 est relié à A et B (entre autres) et M2 à C et D (c'est un minimum nécessaire), alors M3,...,Mk sont superflus, le moins couteux consistant à relier directement M1 et M2.
CQFD. Ouf !
#16 - 21-02-2011 00:51:14
- dhrm77
- L'exilé
- Enigmes résolues : 49
- Messages : 3004
- Lieu: Fanning Island-?-Lac Tele,Mali
Le 4 taupes
Solution 1:
Je positionne les quatre taupes (A,B,C,D) dans un systeme cartesien aux coordonnées suivantes:
A=[0, √3/3, 0]
B=[1/2, -√3/6, 0]
C=[-1/2, -√3/6, 0]
D=[0, 0, √3/6]
Le point d'origine O se trouve donc directement au dessous du sommet de la pyramide.
On peut facilement verifier que les distance A-B, A-C, A-D, B-C, B-D et C-D sont de 1.
Ensuite, je calcule les équations de la droite qui va de A a G, G etant l'epicentre du triangle BCD
(comme O est l'epicentre du triangle ABC)
Les équations sont X=0 et Z=-√2/4Y+√6/12
Le centre de gravité G de la pyramide est le point qui coupe cette droite avec la verticale qui passe par D.
On obtient donc les coordonées de ce point, en combinant ces équations:
G= [0, 0, √6/12]
La distance de G a A est √( (√3/3)^2 + (√6/12)^2 ) = √6/4 = 0.612372436
La distance de G a B est √( (1/2)^2 + (√3/6)^2 + (√6/12)^2 ) = √6/4 = 0.612372436
La distance de G a C est √( (1/2)^2 + (√3/6)^2 + (√6/12)^2 ) = √6/4 = 0.612372436
La distance de G a D est √6/3-√6/12 = √6/4 = 0.612372436
la somme des tunnels est donc √6 = 2.449489743
Cependant ni 0.612 ni 2.449 ne valident....
PS: il m'a fallu griffoner 4 pages de diagrames et calculs pour trouver cette solution....
Solution 2:
Les taupes se retrouvent 2 a 2 quelque part en direction du centre de la pyramide.
Je construit donc entre les points A, B et G un triangle isocele de base 1, et de coté √6/4.
M étant la distance de G a X, et N la distance de X a A, le point X de rencontre d'un groupe de 2 taupes est tel que la distance M + 2 * N est minimale. Apres de long calculs je trouve:
M = (3×√2−2×√3)÷12 = 0.064878256
N = √(1÷12+1÷4) = 0.577350269
d'ou la distance totale des taupes a parcourir = 2*M+4*N = 2.439157588
Great minds discuss ideas; Average minds discuss events; Small minds discuss people. -Eleanor Roosevelt
#17 - 21-02-2011 11:50:08
- gasole
- Elite de Prise2Tete
- Enigmes résolues : 40
- Messages : 1117
- Lieu: Toulouse
les 4 taupeq
Merci pour tes messages, mais je ne les ai vus après avoir abouti, ma solution n'est donc sans doute pas la plus claire possible.
J'ai en effet compris que le site se trompait en découvrant une solution meilleure, mais je n'irai pas jusqu'à généraliser hors du cadre du tétraèdre régulier même s'il me semble que tu as raison avec un tétraèdre quelconque.
Mais es-tu sûr que quelque soit le nombre de points, on va n'utiliser que des PS de degré 3 (par exemple avec des polyèdres bizarres... ) ?
En tout cas, merci de m'avoir fait découvrir cette problématique très intéressante d'optimisation, j'ai appris plein de choses 
#18 - 21-02-2011 12:05:39
- halloduda
- Professionnel de Prise2Tete
- Enigmes résolues : 24
- Messages : 495
- Lieu: Ardèche
#19 - 21-02-2011 12:23:29
- gasole
- Elite de Prise2Tete
- Enigmes résolues : 40
- Messages : 1117
- Lieu: Toulouse
Les 44 taupes
Une dernière remarque histoire de faire du mal aux mouches  On pourrait s'attendre à ce que des taupes cherchent davantage à minimiser le temps passé à creuser qu'à minimiser la distance totale de galeries non ? Or après une jonction elles ne creusent pas deux fois plus vite On pourrait s'attendre à ce que des taupes cherchent davantage à minimiser le temps passé à creuser qu'à minimiser la distance totale de galeries non ? Or après une jonction elles ne creusent pas deux fois plus vite  (au mieux elles creusent une galerie deux fois plus large) (au mieux elles creusent une galerie deux fois plus large)
Pour minimiser le temps, le centre du tétraèdre est un meilleur choix.
#20 - 21-02-2011 17:25:46
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3230
- Lieu: Luxembourg
Les 4 taupe
Bonjour,
J'étais persuadé que la réponse était 4 fois la distance d'un sommet au centre de gravité du tétraèdre (soit V6=2.449 env.), mais cette réponse est refusée.
Et effectivement, cette réponse serait trop simple, mais je sèche complètement.
Je ne vois pas comment la solution ne pourrait pas être "symétrique". Pour le carré, la réponse est plus "visible" (1+V3=2,732 env. et pas 2V2=2,828 env.).
Bonne journée.
Frank
#21 - 22-02-2011 13:29:56
- halloduda
- Professionnel de Prise2Tete
- Enigmes résolues : 24
- Messages : 495
- Lieu: Ardèche
les 4 taupzs
Il était tentant de relier le centre G aux quatre sommets. Ce n'était pas l'optimum.
D'abord une évidence pour interconnecter 3 points ABG avec une longueur minimale.
PA+PB+PG est plus court que GA+GB, pour peu que l'angle AGB soit < 120 degrés.

Appliquons-la avec ABG et CDG dans le tétraèdre, où les angles G valent environ 109 degrés.

AM=√32
MO2=MA2−OA2 ; MO=1sqrt2.
Les noeuds P et Q de la figure sont appelés "points de Steiner".
Comme PO=AO√3, on trouve alors :
longueur creusée = √3+1sqrt2≈2.43916....
La case de vérification validait "2.439".
Cela peut aussi s'appliquer dans un plan (ABCD carré),
pour lequel la distance minimale est 1+√3 et non 2√2.
L'exemple en est donné sur Wikipedia "arbre de Steiner" (donné en indice).
#22 - 22-02-2011 13:36:43
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,039E+3
les 4 taupeq
Désolé, j'ai abandonné avant la fin. Trop dur pour moi. Mais mes préconçus en prennent un coup.
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum











