5^5  =   3125  = 5^(2x3-1)
5^6  =  15625  = 5^(2x6-1-5)
5^7  =  78125  = 5^(2x7+1-8)
5^8  =  390625 = 5^(0+3+9+2-6)
5^9  = 1953125 = 5^(9+5+1-1-2-3)
5^10 = 9765625 = 5^(2x7+5-9+6-6)

Ceci sans utiliser la division ou des parenthèses.

5^1 = 5 = 5
5^2 = 25 = 5^2
5^3 = 125 = 5^(1 + 2)
5^4 = 625 = 5^(6 - 2)
5^5 = 3125 = 5^(3 + 2 * 1)
5^6 = 15625 = 5^((5+1+6) / 2)
5^7 = 78125 = 5^((7+8-1) / 2)
5^8 = 390625 = 5^((9-30/6) * 2)
5^9 = 1953125 = (5^3)^2 * (5*(1+1)-9)
5^10 = 9765625 = 5^(9 + (6+5+2)/(7+6))

Par exemple (mais il y a sans doute plein d'autres possibilités).

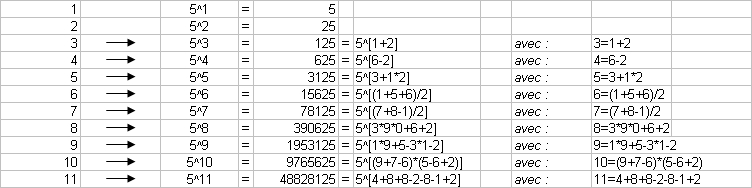
5^1 = 5 = 5
5^2 = 25 = 5^2
5^3 = 125 = 5^(1 + 2)
5^4 = 625 = 5^(6-2)
5^5 = 3125 = 5^(3+1*2) = (3+1*2)^5 (dans l'ordre)
5^6 = 15625 = 5^((1+5+6)/2)
5^7 = 78125 = 5^(17-8-2)
5^8 = 390625 = 5^(9+0-6/2/3)
5^9 = 1953125 = 5^(19-5-3-1*2) = (1+9-5)^((3+1)*2)*5 (dans l'ordre)
5^10 = 9765625 = 5^((9+7+6)/2+5-6) = (9+7+6-5+6+2)^5 (dans l'ordre)
5^11 = 48828125 = 5^(4+8+8+2-8-1-2) = (48/8/2-8)^12/5 (dans l'ordre)
5^12 = 244140625 =5^(2*4+4+1*4+0-6+2) = (((2+4)*4+1)^4+0)*625 (dans l'ordre)
5^13 = 1220703125 =5^(1*2-2+0+7+0+3+1+2) = ((1-2)*2+0+7+0)^(3*1+2*5) (dans l'ordre)
                                                                           = (1+2+2-0-7-0-3)^12*5 (dans l'ordre)
5^14 = 6103515625 =5^(6+1+0+3+5-1*5+6-2) = ((6-10+3)*5)^(1+5+6)*25 (dans l'ordre)
5^15 = 30517578125 =5^(3+0+5-1+7+5+7-8-1-2) = (30+5+1+7*5+7*8-1*2)^5 (dans l'ordre)
5^16 = 152587890625 =5^(1*5-2+5+8-7+8-9+0+6+2) = (1+5+2-5+8-7-8+9+0)^(6+2*5) (dans l'ordre)
5^17 = 762939453125 = 5^(7+6+2+9+3-9+4-5+3-1-2) = (7*6-29-3-9+4)^(5*3*1)*25 (dans l'ordre)
5^18 = 3814697265625 = 5^(38-14+69-72+6-5-6+2) = (3*8-1-4-6-9-7+2+6)^(5+6*2)*5 (dans l'ordre)
etc...
En fait, plus on avance dans les puissances, plus on a de chiffres, et plus ca devient facile de le faire en gardant les chiffres dans l'ordre.

5^4 = 625 = 5^(6-2)
5^5 = 3 125 =5^(2*1*3)
5^6 = 15 625 = 5^((1+5+6)/2)
5^7 = 78 125 = 5^((7+8-1)/2)
5^8 = 390 625 = 5^((2*9+6+0)/3)
5^9 = 1 953 125 = 5^(2+1*3-5+9*1)
5^10 = 9 765 625 = 5^((2+6+5)/(6+7)+9)

5^4 = 625 = 5^(6-2)
5^5 = 3125 = 5^(3*2-1)
5^6 = 15625 = 5^(6*2-5-1)
5^7 = 78125 = 5^(2*7+1-8)
5^8 = 390625 = 5^(9-6+3+2+0)
5^9 = 1953125 = 5^(1*9*2-5-3-1)
5^10 = 9765625 = 5^(6*5-9-7-6+2)

Bravo à tous le monde, comme Tromaril, je me demande comment une telle démonstration peut être possible.
Bravo également à dhrm77, NickoGecko et scarta qui ont fait un peu de zèle en allant au delà de la limite que j'avais fixée.