 |
#1 - 24-01-2011 22:00:51
- Alexein41
- Professionnel de Prise2Tete
- Enigmes résolues : 29
- Messages : 119
Passera passera pas ?
On dispose du circuit électrique suivant :
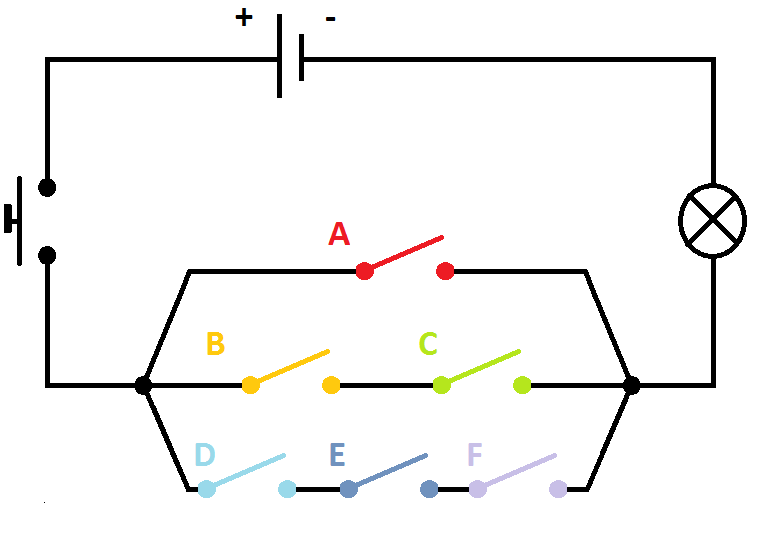
Le bouton poussoir de ce circuit est un peu spécial. Il arrive que quand on appuie dessus, les interrupteurs se ferment.
Les probabilités pour que les interrupteurs A ; B ; C ; D ; E ; F restent ouverts quand on appuie sur le bouton poussoir sont respectivement de 0,3 ; 0,5 ; 0,1 ; 0,8 ; 0,4 ; 0,1.
→ Quelle est la probabilité pour que la lampe s'allume ?
Alexein41. 
#2 - 24-01-2011 22:22:31
- L00ping007
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 2010
- Lieu: Paris
passeta, passera pas ?
Appelons L l'événement la lampe est allumée.
[TeX]L = A \vee (B \wedge C) \vee (D \wedge E \wedge F)[/TeX]
Pour calculer P(L), on va utiliser la formule générale pour X et Y événements :
[TeX]P(X \vee Y) = P(X) + P(Y) - P(X \wedge Y)[/TeX]
On accroche nos ceintures, et on y va ...
[TeX]P(L) = P(A \vee (B \wedge C)) + P(D \wedge E \wedge F) - P((A \vee (B \wedge C)) \wedge D \wedge E \wedge F)[/TeX]
On suppose que les événements sont indépendants (l'énoncé le stipule maintenant, donc c'est OK  ), donc ), donc
[TeX]P(X \wedge Y) = P(X).P(Y)[/TeX]
On obtient donc la formule suivante :
[TeX]P(L) = P(A) + P(B)P(C) - P(A)P(B)P(C) + P(D)P(E)P(F)
- (P(A)+P(B)P(C)-P(A)P(B)P(C))P(D)P(E)P(F)[/TeX]
(j'ai inversé dans mes notations les événements et leur complémentaire, donc pour moi P(A)=0,7 et pareil pour les autres)
P(L) = 0,85282
(que ce fut laborieux ...)
#3 - 24-01-2011 22:46:27
- gasole
- Elite de Prise2Tete
- Enigmes résolues : 40
- Messages : 1117
- Lieu: Toulouse
Passera, passera pas
ça doit être quelque chose comme 0,35628 non ?
Edit :
lol j'ai pris ouvert pour fermé... bon, en parallèle c'est un "ou" et en série un "et", après y plus qu'à prendre les bonnes valeurs. Disons que [latex]P(A)[/latex] est la probabilité que A se ferme (idem pour B,C,...) et [latex]P(on)[/latex] celle que la lampe soit allumée.
Bien sûr on suppose les interrupteurs indépendants, sinon on ne peut rien dire.
En ce cas, on a :
[TeX]P(X\cap Y)=P(X)*P(Y)[/TeX]
et
[TeX]P(X\cup Y) = P(X)+P(Y)-P(X\cap Y) = P(X)+P(\overline{X})*P(Y)[/TeX]
Pour nous, ça donne :
[TeX]P(on)[/TeX][TeX]=P(A\cup (B\cap C) \cup (D\cap E\cap F))[/TeX][TeX]= P(A)+P(\overline{A})*(P(B\cap C)+P(\overline{B\cap C})*P(D\cap E\cap F))[/TeX]
[latex] = 0,85282[/latex] environ
Voici tous mes chiffres significatifs, néanmoins, je m'insurge : si l'expérimentateur n'est pas capable d'estimer la probabilité de fonctionnement des ses interrupteurs au-delà de la première décimale (je doute qu'elles soient exactement égales à des dixièmes) il n'y a aucun sens à calculer la proba globale avec ce degré de précision ! Na ! Bah je rigole, je le pense mais je rigole 
#4 - 24-01-2011 23:02:52
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 5,996E+3
Passera, pssera pas ?
La probabilité qu'elle ne s'allume pas est de
premier circuit 1-0,3 = 0,7
Second circuit 1-(0,5*0,1)= 0,95
Troisième circuit 1 - (0,8*0,4*0,1)= 0,968
Donc 0,7*0,95*0,968 = 0,64372
La probabilité qu'elle s'allume est donc le complément: 35,628 %
ZUT je ne sais pas lire: reste ouvert = pas de lumière !
La probabilité qu'elle ne s'allume pas est donc de
premier circuit (1-0,3) = 0,7
Second circuit (1-0,5)(1-0,1) = 0,45
Troisième circuit (1-0,8)(1-0,4)(1-0,1) = 0,108
Soit 0,7 x 0,45 x 0,108 = 0,03402
La probabilité qu'elle s'allume est de 96,598 %
#5 - 24-01-2011 23:13:49
- fred101274
- Professionnel de Prise2Tete
- Enigmes résolues : 48
- Messages : 163
- Lieu: devant mon écran
PPassera, passera pas ?
Bon alors... en utilisant la formule :
P(XUYUZ) = P(X) + P(Y) + P(Z) - P(XetY) - P(XetZ) - P(YetZ) + P(XetYetZ), cela donne
85,282%
On n’est jamais très fort pour ce calcul...
#6 - 24-01-2011 23:49:24
- fix33
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1198
- Lieu: Devant un clavier depuis 1748
Passea, passera pas ?
Pour 2 relais A et B en parallèle :
Proba[Lampe éteinte] = Proba[A ouvert] x Proba[B ouvert]
Pour 2 relais A et B en série :
Proba[Lampe éteinte] = 1 - Proba[Lampe allumée]
= 1 - Proba[A fermé] x Proba[B fermé]
D'où ici :
Proba[Lampe éteinte] = 0,3 x [1-(1-0,5)x(1-0,1)] x [1-(1-0,8)x(1-0,4)x(1-0,1)]
= 0,3 x 0,55 x 0,892
= 0,14718
Proba[Lampe allumée] = 0,85282
Est-ce bon ?
Telle est la question !

Je ne vien sur se site que pour faire croir que je suis treise intélligens.
#7 - 25-01-2011 01:00:30
- dhrm77
- L'exilé
- Enigmes résolues : 49
- Messages : 3004
- Lieu: Fanning Island-?-Lac Tele,Mali
Passer, passera pas ?
Par ligne, les probabilités que le courant passe sont de .7, .45 et .108
Donc la probabilité que le courant ne passe pas est de .3, .55 et .892
Ce qui donne une probabilite globale de 0.85282 que la lampe s'allume.
Great minds discuss ideas; Average minds discuss events; Small minds discuss people. -Eleanor Roosevelt
#8 - 25-01-2011 03:51:45
- mitsuidewi
- Professionnel de Prise2Tete
- Enigmes résolues : 49
- Messages : 250
- Lieu: dans une chambre universitaire
pasqera, passera pas ?
Je dirai, (en utilisant simplement mes souvenirs de proba, donc ya des chances pour que ce soit très très faux ^^)
Donc, on multiplie chaque ligne indépendamment (B*C et D*E*F), et on additionne les probas de chaque ligne. Ce qui donne 0,382 chances sur 1 que l'ampoule s'allume. Ça me parait plutôt cohérent...
#9 - 25-01-2011 06:54:00
- Fireblade
- Habitué de Prise2Tete
- Enigmes résolues : 0
- Messages : 34
pasdera, passera pas ?
Nous avons besoin de P(BnC) et P(DnEnF) puis P(Au(BnC)u(DnEnF)). En ayant seulement les probabilités citées, on ne peut conclure qu'en cas d'indépendance. Est-ce le cas?
#10 - 25-01-2011 13:10:43
- toni77
- Passionné de Prise2Tete
- Enigmes résolues : 10
- Messages : 65
Passer, passera pas ?
[TeX]\begin{array}{rl}
P(\{la\quad lampe\quad s'allume\})&=P(A)+P(\bar{A}\cap B\cap C)+P(\bar{A}\cap \bar{ B\cap C}\cap D\cap E\cap F)\\
&=P(A)+P(\bar{A})P(B)P(C)+P(\bar{A})(1-P(B)P(C))P(D)P(E)P(F)\\
&=0.7+0.3\times 0.5\times 0.9+0.3\times 0.55\times0.2\times 0.6\times 0.9\\
P(\{la\quad lampe\quad s'allume\})&=\fbox{0.85282}
\end{array}[/TeX]
#11 - 25-01-2011 16:59:27
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3222
- Lieu: Luxembourg
passera, passeta pas ?
Bonjour,
Appelons respectivement a, b, c, d, e et f les probabilités que les interrupteurs A, B, C, D, E et F se ferment (= 1 - celle qu'ils se ferment).
Nous avons a=0,7; b=0,5; c=0,9; d=0,2; e=0,6 et f=0,9.
Il nous faut p(A ou (B et C) ou (D et E et F)).
Comme p(X ou Y ou Z) = p(X) + p(Y) + p(Z) - p(X)*p(Y) - p(X)*p(Z) - p(Y)*p(Z) + p(X)*p(Y)*p(Z), nous avons:
p = a + bc + def - abc - adef - bcdef + abcdef
p = 0,7 + 0,45 + 0,108 - 0,315 - 0,0756 - 0,04860 + 0,034020 = 0,85282
soit p = 85,282 %
Bonne journée.
Frank
#12 - 25-01-2011 17:16:33
- Emigme
- Professionnel de Prise2Tete
- Enigmes résolues : 43
- Messages : 318
passera, oassera pas ?
Il n'y a pas de problèmes : il n'y a que des solutions. Si il n'y a pas de solution, il n'y a pas de problème.
#13 - 25-01-2011 17:54:14
- Nicouj
- Professionnel de Prise2Tete
- Enigmes résolues : 27
- Messages : 330
Passera passera pas ?
edit: merci j'avais lu trop vite fermé au lieu de ouvert.
edit2: j'ai du caca dans les yeux ^^
0.7 + 0.3 * (0.45 + 0.55*0.0.108 ) = 0.85282
#14 - 25-01-2011 19:40:42
- Alexein41
- Professionnel de Prise2Tete
- Enigmes résolues : 29
- Messages : 119
Passera, pasera pas ?
Oula, que de réponses déjà  . .
@L00ping007 : Le principe est bon (même si je n'ai jamais vu cette notation pour la probabilité de l'évènement L ^^) mais ta seconde probabilité est malheureusement vraie. 
@gasole : Non  , je pense que tu as mal lu un petit quelque chose de l'énoncé. , je pense que tu as mal lu un petit quelque chose de l'énoncé.
@gwen27 : Ce n'est malheureusement pas la bonne réponse, relis l'énoncé  . .
@fred101274 : Réponse exacte ! Bravo ! 
@fix33 : C'est exact ! 
@dhrm77 : Exactement ! 
@mitsuidewi : Non, malheureusement  . Relis bien l'énoncé ! . Relis bien l'énoncé ! 
@Fireblade : Oui, désolé, pour moi c'était sous-entendu qu'ils l'étaient, mais il est vrai que ce n'est pas clair. Merci de le préciser  . Je vais le mettre en information supplémentaire. . Je vais le mettre en information supplémentaire.
@toni77 : Ce n'est pas ça. Relis les informations  . .
@Franky1103 : Que dire de plus ? ^^ C'est la bonne réponse  . .
@Enigme :  Très très bien tenté ! Mais on appuie sur le bouton poussoir, ce qui fait que le circuit se ferme à cet endroit-là Très très bien tenté ! Mais on appuie sur le bouton poussoir, ce qui fait que le circuit se ferme à cet endroit-là  . .
@Nicouj : Non  , relis l'énoncé , relis l'énoncé  . .
Spoiler : Indication N'oubliez pas, la probabilité que le courant ne passe pas en A (par exemple) est de 0,3.
NB : Fireblade a eu raison de me demander si les interrupteurs étaient indépendants  . Oui, ils le sont . Oui, ils le sont  . .
Bonne chance à tous ! Alexein41.
#15 - 25-01-2011 19:50:00
- MthS-MlndN
- Hors d'u-Sage
- Enigmes résolues : 49
- Messages : 12,414E+3
- Lieu: Rouen
Passer,a passera pas ?
Tout est indépendant ? Cool ! J'essaye de viser au plus simple 
Proba que le chemin du haut se ferme : [latex]0,7[/latex]
Proba que le chemin du milieu se ferme : [latex]0,5 \times 0,9 = 0,45[/latex] (car les évènements "B se ferme" et "C se ferme" sont indépendants, et qu'on veut les deux forcément pour que tout se ferme)
Proba que le chemin du bas se ferme : [latex]0,2 \times 0,6 \times 0,9 = 0,108[/latex] (idem)
Il y a donc les probabilités suivantes que chaque chemin reste ouvert : [latex]0,3 ; 0,55 ; 0,892[/latex]. Puisque le comportement de chaque chemin est indépendant des autres, la probabilité que les trois chemins restent ouverts est le produit de ces trois probas : [latex]0,3 \times 0,55 \times 0,892 = 0,14718[/latex]
La probabilité que le courant passe, et donc que la lampe s'allume, vaut donc 85,282 %
Podcasts Modern Zeuhl : http://radio-r2r.fr/?p=298
#16 - 25-01-2011 22:10:33
- Alexein41
- Professionnel de Prise2Tete
- Enigmes résolues : 29
- Messages : 119
passera, passera pad ?
@Mths-MlndN : Raisonnement et réponse nickels 
#17 - 25-01-2011 22:37:41
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3500
- Lieu: 94110
pasdera, passera pas ?
Oups !  une petite erreur de calcul. une petite erreur de calcul.
Il ya (1-0.3) = 0.7 chance pour que le courant passe dans le fil A,
(1-0.5)*(1-0.1) = 0.45 chance pour qu'il passe dans le fil B-C,
(1-0.8)*(1-0.4)*(1-0.1) = 0.144 0.108 chance pour qu'il passe dans le fil D-E-F.
Globalement, il y a 0.7 + (1-0.7)*0.45 + (1-0.7-(1-0.7)*0.45)*0.144 0.108 = 0.85876 0.85282 chance pour qu'il passe dans l'un des 3 fils et que la lampe s'allume. 
#18 - 25-01-2011 23:23:27
- franck9525
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1935
- Lieu: 86310
passera, pasdera pas ?
Pour que la lampe s'allume il faut qu'une seule ligne soit fermée
notation:
[TeX]P(A)_{close}[/latex] = (1-0.3)=7 chances sur 10 que ligne A soit fermée
ce qui donne
[latex]P(A)_{close}P(BC)_{open}P(DEF)_{open}
+
P(A)_{open}P(BC)_{close}P(DEF)_{open}
+
P(A)_{open}P(BC)_{open}P(DEF)_{close}
=
\frac{7}{10}.\frac{11}{20}.\frac{892}{1000} + \frac{3}{10}.\frac{9}{20}.\frac{892}{1000} + \frac{3}{10}.\frac{11}{20}.\frac{108}{1000} =\frac{96332}{200000}\approx 48%[/TeX]
The proof of the pudding is in the eating.
#19 - 26-01-2011 07:38:47
- halloduda
- Professionnel de Prise2Tete
- Enigmes résolues : 24
- Messages : 495
- Lieu: Ardèche
passera, passera pzs ?
Les probabilités d'ouverture étant indépendantes, on a :
A ouvert : 0.3
BC fermé: 0.5x0.9=0.45 BC ouvert : 0.55
DEF fermé : 0.2x0.6x0.9=0.108 DEF ouvert : 0.892
Les 3 branches ouvertes =0.3x0.55x0.892=0.14718
La probabilité pour que la lampe s'allume est 0.85282
#20 - 26-01-2011 08:30:11
- Fireblade
- Habitué de Prise2Tete
- Enigmes résolues : 0
- Messages : 34
Passer, passera pas ?
1er trajet  (A)=0,3 (A)=0,3
2e trajet : P(BnC)=0,5x0,1=0,05
3e trajet ; P(DnEnF)=0,8x0,4x0,1=0,032
Au total on a donc : P(Au(BnC)u(DnEnF)=P(A)+P(BnC)+P(DnEnF)-P(An(BnC))-P(An(DnEnF))-P((BnC)n(DnEnF))+P(An(BnC)n(DnEnF)).
P(An(BnC))=0,3x0,05=0,015
P(An(DnEnF))=0,3x0,032=0,0096
P((BnC)n(DnEnF))=0,05x0,032=0,0016
et P(An(BnC)n(DnEnF))=0,3x0,05x0,032=0.00048
Soit P(Au(BnC)u(DnEnF)=0,3+0,05+0,032-0,015-0,0096-0,0016+0,00048
La probabilité que la lampe s'allume est donc de 0,35628
#21 - 26-01-2011 12:48:36
- mitsuidewi
- Professionnel de Prise2Tete
- Enigmes résolues : 49
- Messages : 250
- Lieu: dans une chambre universitaire
Passera, passsera pas ?
Ok je viens de voir que j'ai tout fais à l'envers.
Donc se serait plutot
P = (1-0.8)*(1-0.4)*(1-0.1)+(1-0.5)*(1-0.1)+(1-0.3)
= 0.858
Ca me parait quand meme un peu facile ? ais-je faux ?
#22 - 26-01-2011 16:25:28
- LeSingeMalicieux
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1298
- Lieu: Haute-Marne
pasdera, passera pas ?
Soient les événements :
- A : le courant passe par A
- B : le courant passe par B et C
- C : le courant passe par D, E et F
- L : la lampe s'allume
P(A) = 0,7
P(B) = 0,5 x 0,9 = 0.45
P(C) = 0,2 x 0,6 x 0,9 = 0,108
Il suffit qu'un de ces événements (indépendants) arrive pour que la lampe s'allume.
Il nous faut donc calculer P(L) = P(A U B U C)
Et là... c'est le drame ! Mes cours de probas remontent à un peu trop loin, et surtout je n'ai pas pratiqué depuis...
Donc je sais ce qu'il faut calculer, mais la question est : comment le calculer ?
Avoir quatre mains, c'est plus pratique pour taper sur un clavier.
#23 - 26-01-2011 17:31:13
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1968
Passera, passra pas ?
Edit : Ah, flute, c'est la probabilité que ça reste ouvert et pas fermé
Evénements : A, B, C, D, E, F (l’interrupteur correspondant se ferme)
Pa = 0,7 ; Pb = 0,5 ; Pc = 0,9 ; Pd = 0,2 ; Pe = 0,6 ; Pf = 0,9
L’évènement "La lampe s'allume" correspond à A u B^C u D^E^F
Les évènements A B C D E et F sont indépendants.
P(B^C) = Pbc = 0.5*0.9 = 0.45
P(D^E^F) = Pdef = 0.2*0.6*0.9 = 0,108
P(A ou BC ou DEF) =
Pa + Pbc + Pdef -P(A et BC) -P(A et DEF) -P(BC et DEF) + P(A et BC et DEF)
(principe d'inclusion-exclusion)
Pa + Pbc + Pdef -Pa*Pbc -Pa*Pdef -Pbc*Pdef + Pa*Pbc*Pdef = 85.282 %
La lampe à donc 35,628% de chances de s'allumer
#24 - 26-01-2011 18:26:01
- Tromaril
- Habitué de Prise2Tete
- Enigmes résolues : 20
- Messages : 45
passera, passera pzs ?
Je note X l'événement "l'interrupteur X reste ouvert" et LA l'événement "La lampe s'allume"
[TeX]\overline {LA}=A \cap (B \cup C) \cap (D \cup E \cup F)[/TeX]
Par indépendance, [latex]Pr(\overline {LA})=Pr(A)Pr(B \cup C)Pr(D \cup E \cup F)[/latex]
=[latex]Pr(A)[1-Pr(\overline B)Pr(\overline C)][1-Pr(\overline D)Pr(\overline E)Pr(\overline F)][/latex]
=0,3 x (1-0,5x0,9) x (1-0,2x0,6x0,9)
=0,1472
d'où Pr(LA)=0,8528
Edit : 0,85282 avec tous les chiffres 
#25 - 26-01-2011 18:52:22
- Alexein41
- Professionnel de Prise2Tete
- Enigmes résolues : 29
- Messages : 119
Passera, passera aps ?
@L00ping007 : Ta réponse est maintenant bonne ! 
@gasole : Le résultat est exact  . Si possible, peux-tu donner la réponse avec tous les chiffres significatifs ? . Si possible, peux-tu donner la réponse avec tous les chiffres significatifs ?
@Enigme : En tout cas, j'ai adoré ta réponse ^^.
@NIcouj : C'est presque ça  . Ton résultat est très proche du bon. J'ai compris ta formule et l'erreur se trouve dans le dernier nombre de ta ligne de calcul (celui avant le "=" donc) . Ton résultat est très proche du bon. J'ai compris ta formule et l'erreur se trouve dans le dernier nombre de ta ligne de calcul (celui avant le "=" donc)
-----
@Jackv : Il y a une erreur dans les facteurs de ton dernier produit. Ton résultat est cependant très proche du bon  . .
@franck9525 : Le courant passe quand même si tous les interrupteurs sont fermés, ou même si tous les interrupteurs de deux branches sont fermés. 
@halloduda : Réponse exacte ! 
@Fireblade : Wahou, ça c'est de la formule ! Tu as mis p(A) dans ta formule de la probabilité que la lampe soit allumée, et tu l'as remplacé par 0,3, mais 0,3 est la probabilité que l'interrupteur A soit ... ? 
@mitsuidewi : Ce n'est malheureusement pas la bonne réponse  . Je crois que tu as voulu calculer la probabilité qu'un de ces évènements arrive en faisant p(A u B u C), mais ces probabilités ne s'additionnent pas comme ça . Je crois que tu as voulu calculer la probabilité qu'un de ces évènements arrive en faisant p(A u B u C), mais ces probabilités ne s'additionnent pas comme ça  . .
@LeSingeMalicieux : Tout d'abord, excellente démarche ! Je vais t'envoyer un MP  . .
@scarta : p(A) = 0,3 si l'interrepteur est en position ... ? 
@Tromaril : Exactement  . Je vais être embêtant mais peux-tu donner tous les chiffres significatifs si possible ? ^^ . Je vais être embêtant mais peux-tu donner tous les chiffres significatifs si possible ? ^^
Beaucoup de bonnes réponses et de démarches intéressantes ! Les erreurs sont surtout des étourderies ^^.
Spoiler : Indication n°2 0,3 est la probabilité que l'interrupteur A soit ouvert et non fermé ! 
Alexein41.
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum







