Bon effectivement je m'y suis mal pris...

Alors supposons que l'ampoule s'allume si au moins une des 3 branches conduit le courant.
donc :
Soit A : {la branche A est fermée)
      B : {la branche B est fermée)
      C : {la branche C est fermée)
[TeX]P(au \; moins \; 1 \; des \; 3\; soit \; ferm\acute{e}) = 1 - P(\bar{A}\; \cap\; \bar{B}\; \cap \;\bar{C})
=1-[P(\bar{A})*P(\bar{B})*P(\bar{C})]
=0.99952[/TeX]

Juste un "petit" peu ? parce que je trouve presque la même chose là !

Merci beaucoup pour la petite piqûre de rappel en MP Alexein41

Je dois donc calculer P(L) avec :
P(L) = P(A u B u C) = p(A) + p(B) + p(C) - p(A n B) -p(A n C) - p(B n C) + p(A n B n C)

soit P(L) = 0,7 + 0,45 + 0,108 - 0,7 * 0,45 - 0,7 * 0,108 - 0,45 * 0,108 + 0,7 * 0,45 * 0,108

soit P(L) = 0,85282

La lampe a donc un peu plus de 85% de chance de s'allumer

Beaucoup de bonnes réponses ! Tout d'abord, merci à tous de vôtre participation !

Personnellement, j'ai trouvé 2 démarches pour aboutir au résultat :

1ère méthode :

On note A ; B ; C ; D ; E ; F les évènements "l'interrupteur X est fermé".
On a p(A) = 0,7 ; p(B) = 0,5 ; p(C) = 0,9 ; p(D) = 0,2 ; p(E) = 0,6 ; p(F) = 0,9.

Comme les évènements A ; B ; C ; D ; E et F sont tous indépendants, on a :
p(B n C) = p(B) * p(C) = 0,45
et p(D n E n F) = p(D) * p(E) * p(F) = 0,108

On note p(P) la probabilité que la lampe s'allume.
On a alors : p(P) = p(A u (B n C) u (D n E n F))

Sachant la formule suivante : p(X u Y u Z) = p(X) + p(Y) + p(Z) - p(X n Y) - p(X n Z) - p(Y n Z) + p(X n Y n Z), on a la (grande) formule suivante :

p(P) = p(A) + p(B n C) + p(D n E n F) - p(A n (B n C)) - p(A n (D n E n F)) - p((B n C) n (D n E n F)) + p(A n (B n C) n (D n E n F).

Je vous épargne le calcul ^^, et on trouve p(P) = 0,85282.

2ème méthode :

On note P1 ; P2 ; P3 les évènements "Le courant passe dans la branche Pn." et on reprend les autres notations du haut.
On a p(P1) = p(A) = 0,7
p(P2) = p(B n C) = p(B) * p(C) = 0,45 (indépendance des évènements)
p(P3) = p(D n E n F) = p(D) * p(E) * p(F) = 0,108 (indépendance des évènements).

On obtient l'arbre de probabilités suivant :



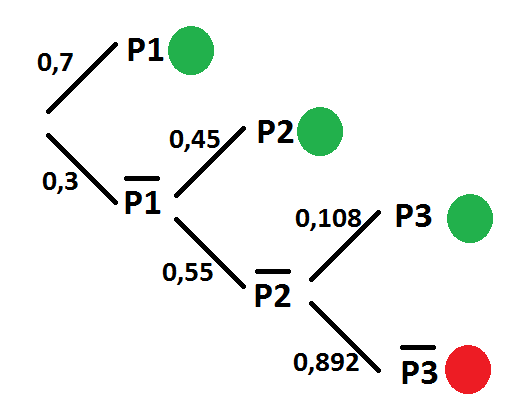
Les ronds verts désignent les moments où le courant passe (contrairement au rond rouge).

1ère solution :

p(P) = 0,7 + 0,3*0,45 + 0,55*0,108 = 0,85282 (en utilisant les probabilités conditionnelles)

2ème solution :

p(P) = 1 - 0,3 * 0,55 * 0,892 = 0,85282 (p(P) désigne le contraire de la probabilité que le courant ne passe dans aucune des 3 branches).

Voilà voilà, vous savez tout . Merci à tous ceux qui ont participé ! Alexein41

La prochaine fois, on reliera la pile directement à la lampe, promis !

Euh excellente question ! En faisant la seconde méthode, moi je pensais juste à faire un joli arbre de probabilités ^^.
Mais d'après ce que je viens de lire, je n'en suis pas sûr