Enigme Nervures optimales @ Prise2Tete

Clydevil · #1

Hello hello, une petite question que je me posais, si quelqu'un connaît le mot clef d'un problème mathématique connu qui s'en rapproche ça me plaira aussi de le connaître:

On considère un disque de diamètre unité. Le but est de construire un réseau connexe de longueur totale 1 qui minimise la distance la plus grande entre un point du disque et le point le plus proche du réseau.
Par exemple:
-Si notre réseau est un diamètre, les points du disque les plus éloignés du point du réseau le plus proche d'eux sont les extrémités du diamètre perpendiculaire et se trouve à 1/2
On peut bien sur faire mieux que ce 1/2 avec un + au centre par exemple ou un cercle de même centre que notre disque.
Si ce problème ne vous évoque rien vous pouvez toujours tentez de poster une belle image du mieux que vous trouverez par vous même

Éléments de réponse:
Spoiler : [Afficher le message]

Annonces sponsorisées :

nodgim · #2

Y aurait il une meilleure solution que le cercle de périmètre 1 centré au milieu ?

MthS-MlndN · #3

D'instinct, je pense qu'un cercle dont le centre est le centre du disque minimisera la distance, parce que les points les plus gênants seront ceux qui se trouvent à l'extrémité du disque...

Mais peut-être que je me trompe, je n'en sais rien

Le problème me semblerait plus tordu avec un réseau connexe de taille plus grande (typiquement supérieure au périmètre d'un cercle de diamètre 1/2).

Clydevil · #4

Une bonne remarque, il me semble cependant avoir trouvé mieux que le cercle :p
(une forme simple, je peux toujours vous la donner sur PM si besoin)

@MthS-MlndN: oui pour une longueur quelconque ça peut très vite dégénérer

nodgim · #5

En effet, en ouvrant le cercle sur un secteur de 142 ° environ, et en remplaçant l'arc correspondant en 2 1/2 segments, on gagne 0.07 max en longueur, gain qui peut s'exprimer par une augmentation du rayon de ce cercle entre 0.01 et 0.02.

NickoGecko · #6

Bonjour,

Je prends mon tour mais je n'ai pas mieux que le cercle de circonférence unitaire pour le moment.

Je l'ai illustré ainsi que le "+" au centre et j'ai aussi essayé un "I" (ou H) pour voir !

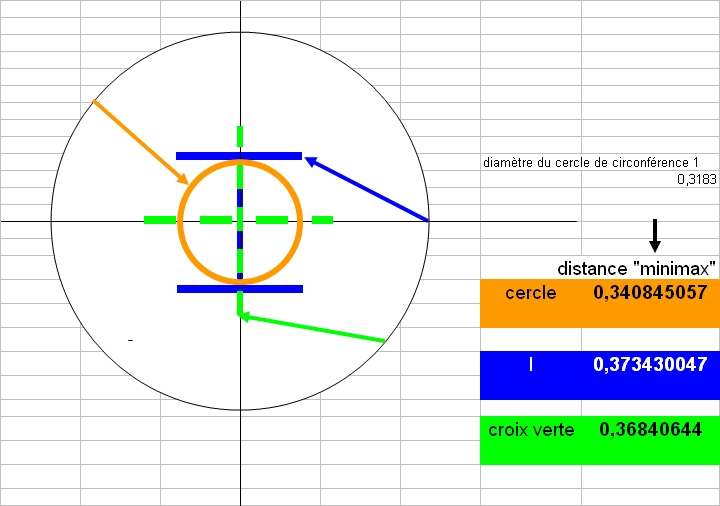
Ah si le réseau ne devait pas être connexe, on pourrait placer des segments disjoints en plein milieu !

A bientôt si éclair de génie ....

Clydevil · #7

Ajout d'éléments de réponse dans le post original.

Vasimolo · #8

La solution que tu proposes m'a fait penser à ce problème assez proche http://www.prise2tete.fr/forum/viewtopic.php?id=4703

Vasimolo

nodgim · #9

Clydevil a écrit:
Ajout d'éléments de réponse dans le post original.

Dans ton message du 1er message, as tu cherché à optimiser l'orientation des segments ? il me semble que le mieux est de les avoir tangents au cercle, mais...

Clydevil · #10

@Nodgim:
Oui bien sur que j'ai regardé ce que donnait l'orientation des segments**, cette orientation change avec la longueur autorisée mais je crois qu'elle ne donne généralement pas de segments tangents au cercle, peut être que ce sont des segments qui pointent vers le point du cercle équidistant des extrémités de chacun. (Ce qui dans le cas limite de ma figure tout à fait spécial donne des segments tangents, la figure est donc fausse) A méditer.

**Me suis peut être totalement piné, faudrait poser les calculs.

Je suis surtout curieux de la tête du réseau si on autorise une longueur de 10...

Clydevil · #11

EUREKA:
Enfin début d'idée pour aborder le probleme!
C'est très con, mais en fait fondamental, je me suis rendu compte que le probleme est récursif:
Si on considère une sous partie de notre réseau SR et la partie non desservie de notre forme par le complémentaire de ce sous réseau A, SR doit être de longueur minimal pour couvrir A. (avec une petite contrainte en plus qu'il doit passer par le point commun avec la suite du réseau).

Je sais pas si je suis très clair, mais en gros ca formalise un peu dans notre probleme particulier qu'un sous partie d'une solution optimale est aussi optimale.

Ça permet d'obtenir des optimums locaux, des solutions non trivialement stupide.

nodgim · #12

Si tu trouves une soluce avec un segment extérieur à la tangente (car intérieur à la tangente n'a pas de sens), alors on peut tracer un autre segment plus court entre l'extrémité du segment et la tangente, cet autre segment étant valable puisque extérieur au 1er segment et donc plus proche du cercle extérieur.
CQFD

Forum dédié aux énigmes et à toutes formes de jeux de logique.	Déconnexion
Tu n'es pas identifié sur Prise2tete : s'identifier. Accueil Forum	[+]

#1 - 18-09-2011 14:07:36

nervures optimzles

#0 Pub

#2 - 18-09-2011 15:14:35

Nevrures optimales

#3 - 18-09-2011 15:56:32

nervured optimales

#4 - 18-09-2011 16:13:46

Nervues optimales

#5 - 19-09-2011 19:07:47

ervures optimales

#6 - 20-09-2011 07:57:16

Neruvres optimales

#7 - 21-09-2011 14:28:50

Nervrues optimales

#8 - 21-09-2011 16:31:10

Nervures optimalles

#9 - 21-09-2011 19:19:09

nervures optimakes

Clydevil a écrit:

#10 - 21-09-2011 23:17:48

Nervures optimals

#11 - 22-09-2011 17:32:36

nervures ootimales

#12 - 22-09-2011 18:27:26

Nevrures optimales

Réponse rapide

Sujets similaires

Pied de page des forums