 |
#1 - 08-12-2012 18:22:55
- birmo
- Amateur de Prise2Tete
- Enigmes résolues : 0
- Messages : 8
Prooblèmes de triangles
Bonjour à tous,
Je suis un grand lecteur de prise 2 têtes bien que je n'ai jamais encore posté de message, alors je commence aujourd'hui !
Ce problème est issue du rallye mathématiques de Bourgogne 2007 :
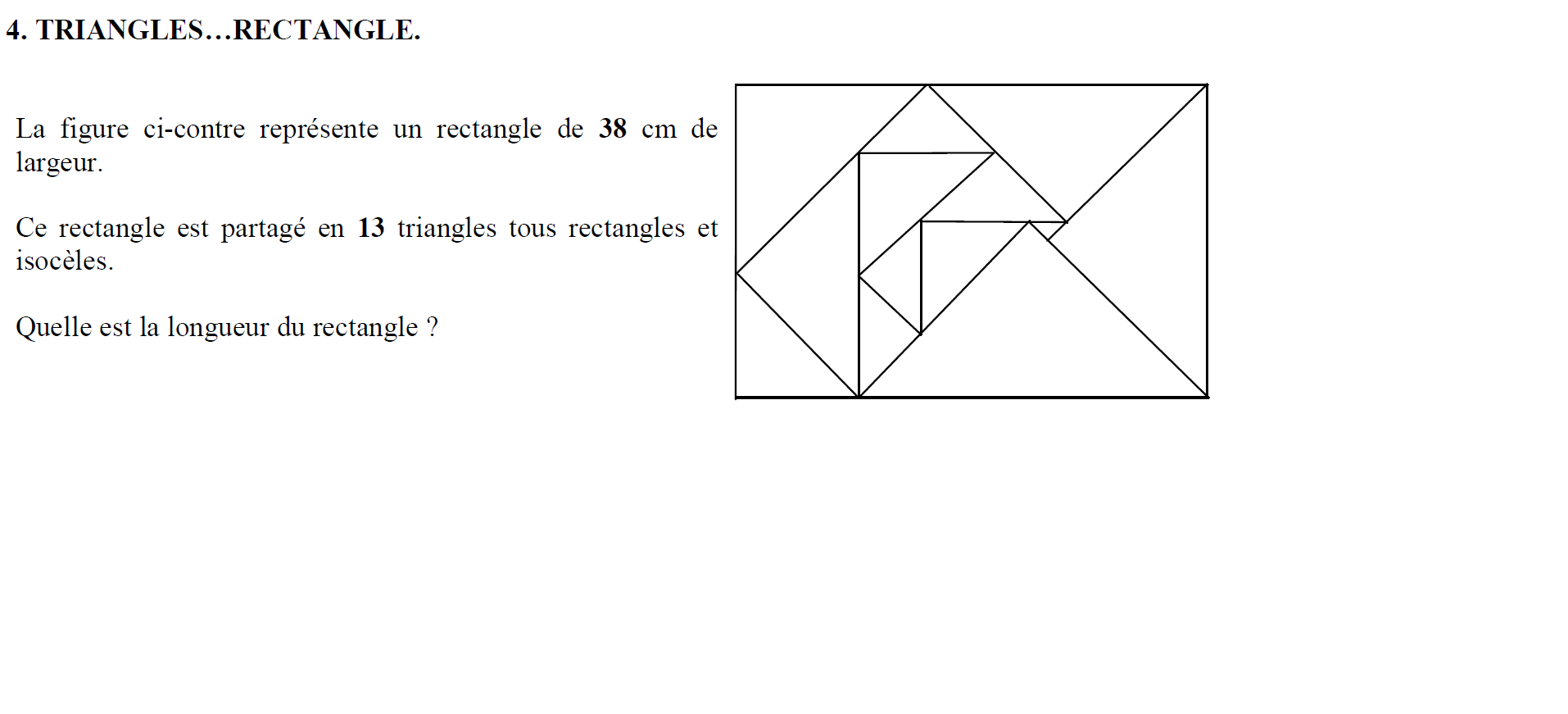
Je vous donnerais une élégante solution tirée du livre "100 gourmandises mathématiques" de Robert Ferachoglou et Michel Lafond, mais j'ai hâte de voir les votres, bonne chance !
#2 - 08-12-2012 19:22:56
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3230
- Lieu: Luxembourg
problèmes de trianglzs
Bonjour,
J'appelle a l'hypothénuse du triangle de droite et b celle du plus petit triangle au milieu. En écrivant les égalités successives entre les côtés et l'hypothénuse de chacun des triangles, on arrive à décomposer les côtés supérieur et inférieur du rectangle en (a/2+b)+(a-b) et (a/2-b)+(a+b) qui valent tous deux 3a/2.
La longueur du riangle est donc de: 38 x 3 / 2 = 57 cm.
Bonne soirée.
Edit: correction d'une faute d'orthographe.
#3 - 08-12-2012 19:24:16
- gilles355
- Professionnel de Prise2Tete
- Enigmes résolues : 49
- Messages : 421
problèmes de troangles
Bon ben j'ai été devancé mais voici sans détails la réponse en dessin:
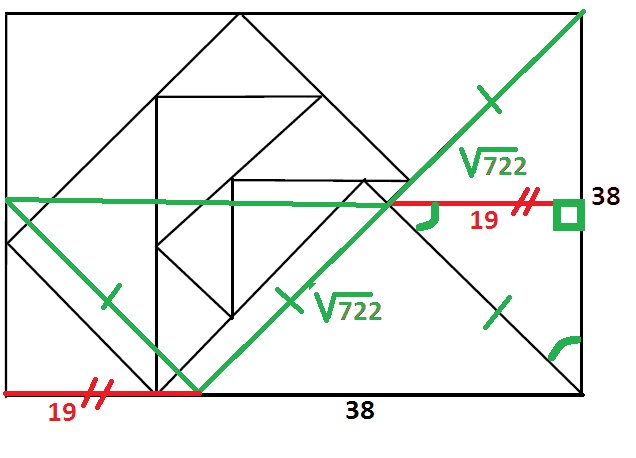
#4 - 08-12-2012 20:10:59
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
Problèmes de trianggles
Bien vu Gilles !
ça fleurait l'arnaque tous ces triangles...
Je tiens à signaler que Michel Lafond est très actif sur le site de Diophante. Si le coeur vous en dit, allez y; Attention, c'est assez souvent du haut niveau...
#5 - 08-12-2012 20:17:13
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3230
- Lieu: Luxembourg
Prbolèmes de triangles
Comparée à la grosse armada que j'ai mise en oeuvre, la solution de gilles355 est très élégante: bravo. Je n'avais pas vu cette petite astuce.
#6 - 08-12-2012 20:26:53
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
Prroblèmes de triangles
Bon, désolé mais je ne comprends pas pourquoi le triangle tout vert est inscrit entièrement dans la figure...
La figure donne l'impression qu'il sort un peu sur al gauche, et en y regardant de plus près, je ne vois rien qui indique que le sommet de gauche se trouve exactement sur le côté de la figure générale...
Il y a quelque chose qui le prouve facilement ?
#7 - 08-12-2012 20:46:51
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
Problèmes de ttriangles
Gilles, je pense qu'il y a un problème dans ta démo (ou un gros non-dit qui m'échappe).
Apparemment, tu n'utilises que le premier triangle rectangle, ce qui voudrait dire que ce résultat serait valable pour n'importe quel rectangle de largeur 38 (et ça ce n'est pas possible).
En fait, je pense que tu ne prouves pas que le côté du triangle à gauche vaut √722.
#8 - 08-12-2012 20:59:40
- birmo
- Amateur de Prise2Tete
- Enigmes résolues : 0
- Messages : 8
problèmes de trianhles
Bien joué à vous !
La solution proposée dans le livre précédemment cité est la suivante :
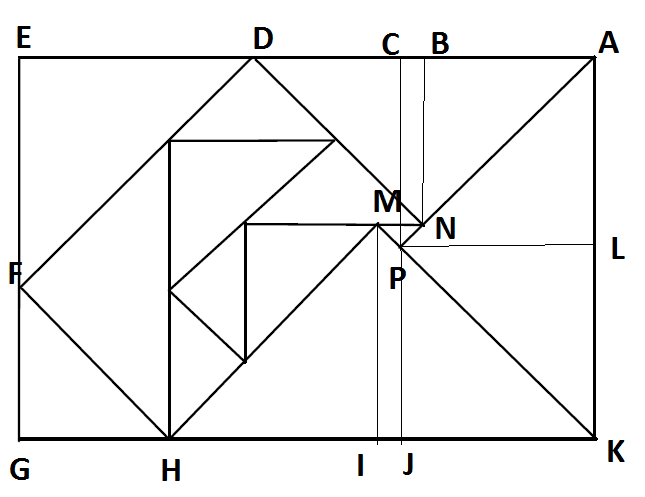
On pose MN = 2x
Puisque AK = 38 on a
JK = PL = CA = KL = LA = 19
HI = KI = KJ + JI =19+x
DB = AB = AC-CB = 19-x
ED + GH = EF + FG = EG = 38
Le double de la longueur est alors :
EA + GK = (ED + DB + BA) + (GH + HI + KI)
= (ED +GH) + (DB+BA) + (HI+KI)
Soit EA + GK = 38 + 2(19-x) + 2(19+x) = 114
Donc la longueur égale 114/2 = 57 cm
#9 - 08-12-2012 22:35:01
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,037E+3
roblèmes de triangles
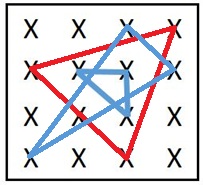
J'ai tendance à aimer la démonstration de gilles en partant du cas limite du triangle 1, même s'il manque un maillon, elle est très simple et sans aucun calcul (même rac(722) )
#10 - 08-12-2012 22:49:21
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
Problèems de triangles
Gwen, ça te dérangerait de donner ton raisonnement pour arriver à 57 stp merci ? 
#11 - 08-12-2012 22:54:42
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,037E+3
Problèems de triangles
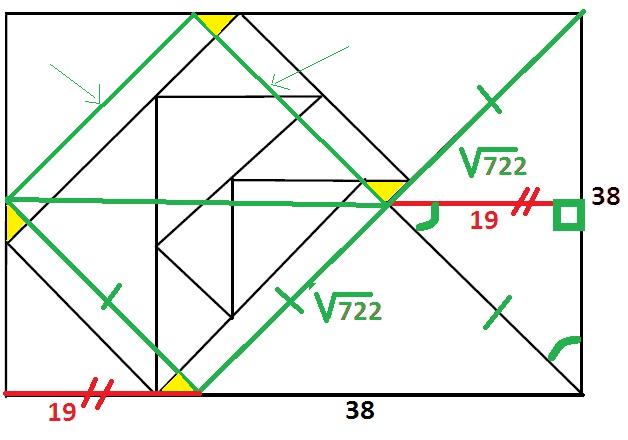
En prenant le triangle 1 et les traits rouges (prolongements directs : on arrive à 1/3 2/3 soit 19x3=57
En décalant la limite du triangle noir, on se contente de le reporter sans changer le rapport global. Et peu importe les 8 triangle intérieurs (qui peuvent varier d'ailleurs, je pense)
Pris à l'envers, le problème est le même, je pars des triangles en couleur, je retombe sur le "poisson" 1/3 2/3
Il manque juste les deux traits verts fléchés pour rendre la démonstration imparable.
#12 - 08-12-2012 23:36:40
- birmo
- Amateur de Prise2Tete
- Enigmes résolues : 0
- Messages : 8
Prbolèmes de triangles
Au fait je cherchais un moyen de résoudre ce problème mais en calculant pas à pas les longueurs de chaque triangle. Mais je galère 
Par exemple voyez-vous un moyen de trouver la mesure du segment ED (cf mes notations du message précédent) ? A ce point on ne connait toujours pas la réponse (57 cm).
#13 - 09-12-2012 00:01:38
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3230
- Lieu: Luxembourg
Problèmes de trinagles
@birmo:
J'avais fait un calcul pas à pas en posant AK = a et MN = b.
En passant les calculs intermédiaires, j'avais trouvé:
ED = EF = a/2 + b; DA = a - b; GH = GF = a/2 - b et HK = a + b.
Au final on a: EA = ED + DA = 3a/2 = 57 et GK = GH + HK = 3a/2 = 57.
Comme le "b" a été éliminé (et c'est pareil avec la solution de l'auteur), on peut penser qu'en changeant MN le résultat final restera 57. Et du coup, on ne peut pas calculer ED qui varie en fonction de MN. On voit d'ailleurs bien sur le schéma de gwen27 que MN peut varier sans changer la valeur 57.
#14 - 09-12-2012 00:35:53
- birmo
- Amateur de Prise2Tete
- Enigmes résolues : 0
- Messages : 8
problèmrs de triangles
Merci pour ta réponse, à force d'essayer je pensais aussi que ce n'était pas possible de donner une mesure de ED.
J'avais envie de trouver un moyen car les auteurs indiquent dans le livre "
Les longueurs de tous les segments de la figure peuvent être calculées ; on trouve par exemple : ED = 23 et FG = 15. "
Cependant ils n'indiquent pas comment ... alors j'imagine que c'est une erreur ?
#15 - 09-12-2012 08:24:01
- dylasse
- Professionnel de Prise2Tete
- Enigmes résolues : 21
- Messages : 378
Problèmes d etriangles
Je poste ma réponse car... malgré plusieurs lectures, je n'ai pas vu le truc du parallélogramme qui glisse sur les bords du rectangle.
Et bien que plus calculatoire ma démo n'est pas trop longue;)
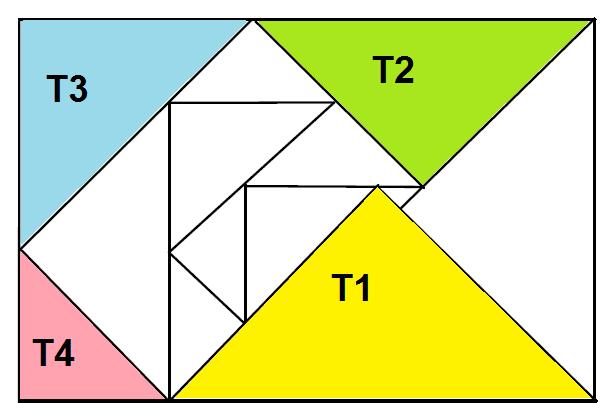
J'appelle h1 et h2 les hauteurs de T1 et T2. On voit que h1+h2 = 38.
J'appelle c3 et c4 les cotés de T3 et T4, on a c3 + c4 = 38.
Dans le sens de la longueur, on a aussi : L = c3 + 2 x h2 (en haut) et L = c4 + 2 x h1.
Donc 2 x L = 2x(h1+h2) + c3+c4 = 2 x 38 + 38
Et finalement, L = 57 cm
Bon, je vais quand même relire les démo au dessus !!!
#16 - 09-12-2012 11:27:40
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
Problèmes de trianglse
J'aime beaucoup ta démo Dylasse !
D'ailleurs, je n'ai toujours pas compris pourquoi la tête du poisson de Gwen ne sort pas de la figure de base (ou au contraire n'est pas en retrait)... 
#17 - 09-12-2012 12:32:51
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Problèmes de trianglles
C'est vrai que la démo de Dylasse est super sympa 
Personnellement je n'ai pas encore cherché , j'essaie encore de dessiner proprement l'objet .
Vasimolo
#18 - 09-12-2012 19:58:58
- geotrouvetou
- Amateur de Prise2Tete
- Enigmes résolues : 32
- Messages : 2
Problèmes de tringles
La longueur est de 57 cm.
#19 - 09-12-2012 22:30:15
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
Problèmes de rtiangles
golgot59 a écrit:J'aime beaucoup ta démo Dylasse !
D'ailleurs, je n'ai toujours pas compris pourquoi la tête du poisson de Gwen ne sort pas de la figure de base (ou au contraire n'est pas en retrait)... 
figure dynamique sous geogebra
Dans la "démo" de gwen, ce qui explique que le "poisson" loge pile dans le cadre, ce sont les 3 petits triangles identiques à MNP. En les plaçant dès le début, on comprend pourquoi le carré rouge loge pile poil : c'est ce que je n'avais pas compris au départ sans explication. Après, la solution vient facilement.
#20 - 09-12-2012 23:31:28
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
Problèmes de trianggles
Mieux que des mots : Une démo !
Merci Titou. Effectivement, le graphique parle de lui même, et heureusement, car l'écrire noir sur blanc compliquerait pas mal cette jolie démonstration graphique...
Avec un peu de retard, bravo Gwen 
#21 - 09-12-2012 23:45:05
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Probblèmes de triangles
Il y a plein de démonstrations du fait que trois largeurs font deux longueurs ( j'en ai quelques autres ) mais bizarrement contrairement à ce qu a été affirmé la figure est unique .
Vasimolo
#22 - 10-12-2012 16:51:40
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3230
- Lieu: Luxembourg
prpblèmes de triangles
@Vasimolo
Veux tu dire par là que le remplissage (en lignes brisées) du quasi-rectangle de gauche (le corps du poisson) n'est pas que de la déco et contraint le dessin global
à être unique ?
#23 - 10-12-2012 18:40:12
- birmo
- Amateur de Prise2Tete
- Enigmes résolues : 0
- Messages : 8
Problèmes de triiangles
Mais si la figure est unique il devrait y avoir un moyen de connaître la mesure des longueurs de chaque triangle non ? Parce que s'il y avait un moyen de connaître ED je serais vraiment heureux de le connaître 
#24 - 10-12-2012 19:45:28
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Problèmes de trianges
Voilà les calculs que j'avais fait hier , ou plutôt les résultats , je vous laisse chercher un peu 

Vasimolo
#25 - 10-12-2012 20:07:53
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
Problèmes de trianglles
J'ai fait un calcul tout bête de proche en proche, en utilisant NP = a et M jusqu'au point de gauche du triangle dont un coôté est aligné avec MN = b
A partir de là tout se calcul facilement en fonction de a et b, c'est d'ailleurs étonnant de voir comme les longueurs des côtés se simplifient !
On obtient à la fin 2 équation à 2 inconnues en égalant chaque côté du rectangle à 38.
Je trouve comme Vasimolo avec a=2√2 et b=14
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum













