 |
#1 - 08-01-2018 21:52:56
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Un ts de triangles équilatéraux + INDICE
Bonjour à tous.
Voici un problème trouvé dans la revue "Tangente" (qui le tient de "La Recherche", mais je n'en sais pas plus). Comme j'ai remarqué qu'il existe une démonstration élémentaire (compréhensible par un élève de seconde, mais pas forcément évidente à trouver), je me suis permis de vous le soumettre.
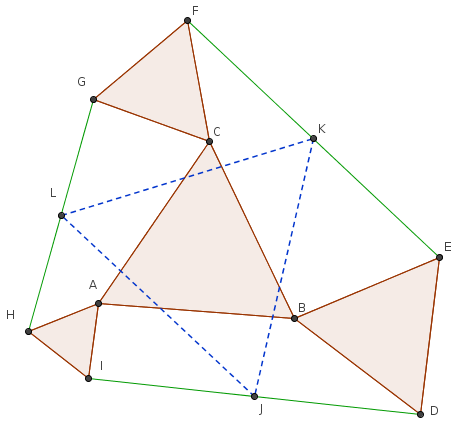
Les quatre triangles rouges sont équilatéraux, peu importent leurs dimensions ou orientations. Les points J, K et L sont les milieux respectifs de [DI], [EF] et [GH].
Démontrer que le triangle JKL est équilatéral.
INDICE : Spoiler : [Afficher le message] 
#2 - 10-01-2018 22:41:39
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
un tas de yriangles équilatéraux + indice
Bonsoir Ebichu
Je n'ai pas de réponse complète mais il est clair que si on se donne le triangle ABC et deux des points J, K et L alors le troisième point s'impose ( quelque soit la position des trois autres triangles ) . Il reste à trouver pourquoi JKL est équilatéral 
Vasimolo
#3 - 10-01-2018 23:03:27
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
un tas de triangles équilatérauw + indice
@Vasimolo : je suis d'accord avec ton affirmation, mais ça ne me paraît pas "clair" ; en y réfléchissant 5 minutes, je ne vois pas comment je pourrais la démontrer autrement qu'en démontrant le problème initial.
En tous cas la remarque est intéressante, et je te souhaite de réussir à en tirer une solution.
#4 - 11-01-2018 08:57:33
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
un tas de triangleq équilatéraux + indice
Je ne sais pas par quel bout le prendre pour l'instant....
#5 - 11-01-2018 09:58:16
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
un tas de triangles équilatéraux + indixe
@nodgim : j'ai aussi mis un bon bout de temps avant de voir comment aborder ce problème. Je laisse encore un peu de temps, puis je mettrai un indice. Simplement savoir quel outil utiliser devrait suffire.
#6 - 11-01-2018 12:31:16
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Un tas de triangles équilatéraux + INDIC
#7 - 11-01-2018 15:16:27
- LeJeu
- Passionné de Prise2Tete
- Enigmes résolues : 25
- Messages : 77
Un tas de triangle équilatéraux + INDICE
Bonjour les champions !
j'entrevois bien que la solution qui pour l'instant échappe à Vasimolo et à Nodgim est définitivement hors de portée pour moi..
Néanmoins, petit colibri, je fais ma part de travail...
j'ai trouvé sur www.ilemaths.net le problème sous une forme " dégénérée" : le premier triangle est un point , et les trois autres ont même coté :
"Si ABCDEF est un hexagone inscrit dans un cercle C(0,R), de sorte que AB=CD=EF=R, alors les milieux respectifs P,Q,R des segments [BC],[DE],[FA], sont les sommets d'un triangle équilatéral. "
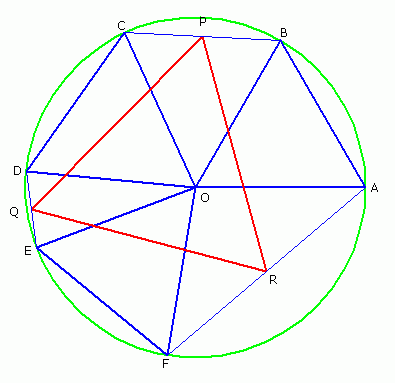
Et déjà les solutions proposées ne sont pas triviales :
- une en passant par les nombres complexes : https://www.ilemaths.net/sujet-triangle … 96461.html
- l'autre en passant par AlKashi : https://www.ilemaths.net/sujet-nombres- … 96395.html
Je suis impatient de vous lire, pour savoir comment aborder le cas général
Salutations
#8 - 11-01-2018 16:45:23
- LeJeu
- Passionné de Prise2Tete
- Enigmes résolues : 25
- Messages : 77
Un tas de tirangles équilatéraux + INDICE
Ceci-dit,il me semble que
1) si on monte que la proposition est vraie pour un triangle de départ( celui qui touche les 3 autres) de taille nulle, alors par une sorte "d'expansion" , on doit pouvoir montrer "facilement ?" qu'elle sera encore vraie pour un premier triangle de taillle non nulle ?
2)De là, une idée serait de partir de la forme dégénérée précédente, et de montrer que la proposition est toujours vraie quand les trois triangles ne sont plus égaux, en dessinant par exemple trois triangles égaux à l'intérieur ( la taille du plus petit par exemple)
Un premier dessin semble confirmer que la proposition 2 est une bonne piste
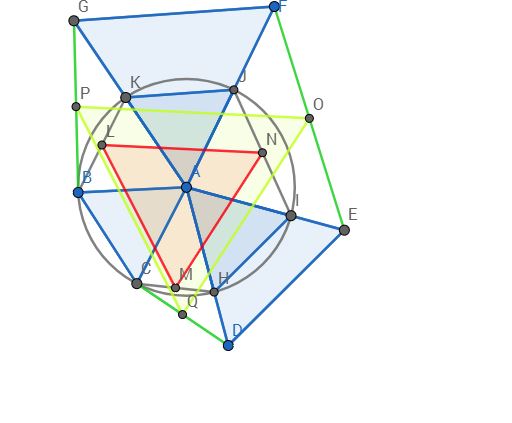
les trois triangles de départ sont
ABC ADE AFG
on dessine ABC AHI AKJ
c'est le cas dégénéré de mon post précédent
donc LMN est equilatéral
on trace le triangle final POQ
ne "reste plus " à démontrer que les cotés sont bien parallèle à LMN
et donc que POQ est bien équilatéral
Je sais , ça fait beaucoup de supposition.... toutes mes excuses.. je n'ai pas la possibilité à l'instant d’approfondir....
[Edit]Après approfondissement tout faux.. les cotés des deux triangles ne sont pas du tout parallèles dans le cas général, mon dessin était un cas particulier
#9 - 11-01-2018 18:04:07
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Un tas de triangles équiilatéraux + INDICE
@Vasimolo : ça me coupe la chique, j'aurais été bien incapable d'imaginer ce joli raisonnement. Dommage que ça ne permette pas (encore ?) de conclure. Bien sûr, je ne donnerai pas d'indice tant que tu seras encore en train de chercher.
@LeJeu : c'est effectivement une version dégénérée de ce problème. Par conséquent, ma démonstration s'adapte très bien à la version dégénérée, et elle est bien plus élémentaire que les deux solutions auxquelles tu fais référence.
Pour ton deuxième message, c'est une idée, mais pour l'instant il n'est pas certain que cela suffise à conclure. Il faut creuser, bon courage.
#10 - 13-01-2018 22:36:47
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
U ntas de triangles équilatéraux + INDICE
Salut !
Bon, après des heures de recherche infructueuses, j'ai décidé d'employer la grosse cavalerie : La géométrie complexe.
Alors on choisi pour repère orthonormé directe (A, AB->, le vecteur qui va bien)
Alors : zA = 0 et zB = 1 et zC = e^(iπ/3)
On choisi comme variable zF, zD et zH.
On obtient par rotation complexe :
zG = (zF-zC)e^(iπ/3)+zC = (zF-e^(iπ/3))e^(iπ/3)+e^(iπ/3)
= zF.e^(iπ/3)-e^(i2π/3)+e^(iπ/3) = zF.e^(iπ/3)-e^(i2π/3)+e^(iπ/3)
= zFe^(iπ/3)+1
zE = (zD-zB)e^(iπ/3)+zB = (zD-1)e^(iπ/3)+1 = zD.e^(iπ/3)-e^(iπ/3)+1
= zD.e^(iπ/3)+e^(-îπ/3)
zI = (zH-zA)e^(iπ/3)+zA = zH.e^(iπ/3)
zK = (zF+zE)/2 = .5[zF+zD.e^(iπ/3)+e^(-iπ/3)]
zJ = .5[zD+zH.e^(iπ/3)]
zL = .5[zH+zF.e^(iπ/3)+1]
reste à calculer les longueurs :
2.LK = |zF+zD.e^(iπ/3)+e^(-iπ/3)-zH-zF.e^(iπ/3)-1|
= |zD.e^(iπ/3)+zF.e^(-iπ/3)-zH+e^(-i2π/3)|
2.KJ = |zD+zH.e^(iπ/3)-zF-zD.e^(iπ/3)-e^(-iπ/3)|
= |zD.e^(-iπ/3)-zF+zH.e^(iπ/3)+e^(2iπ/3)|
= |e^(-i2π/3)||zD.e^(iπ/3)-zF.e^(i2π/3)+zH.e^(3iπ/3)+e^(4iπ/3)|
= |zD.e^(iπ/3)+zF.e^(-iπ/3)-zH+e^(-2iπ/3)|
2.JL = |zH+zF.e^(iπ/3)+1-zD-zH.e^(iπ/3)|
= |zD.e^(iπ)+zF.e^(iπ/3)+zH.e^(-iπ/3)+1|
= |e^(i2π/3)||zD.e^(iπ/3)+zF.e^(-iπ/3)+zH.e^(-i3π/3)+e^(-i2π/3)|
= |zD.e^(iπ/3)+zF.e^(-iπ/3)-zH+e^(-i2π/3)|
Donc JL = KJ = LK, JLK est équilatéral
Je suis quand même bien déçu de ne pas avoir trouvé l'astuce qui évite ces calculs laborieux. 
#11 - 14-01-2018 00:05:34
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
un tas de triangles équilatéraux + indive
@golgot59 : bravo ! Effectivement, c'est un peu bourrin, mais ça marche 
La démo de Tangente utilisait la même "grosse cavalerie", d'une manière un peu différente. Je comprends ta frustration, car si ces méthodes calculatoires sont efficaces, à la fin, on n'a pas toujours l'impression d'avoir compris ce qui fait que ça fonctionne. C'est du fait de ce sentiment que j'ai cherché une démonstration plus éclairante.
#12 - 14-01-2018 11:01:53
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
UUn tas de triangles équilatéraux + INDICE
Je n'ai pas renoncé à une démonstration géométrique mais pour me rassurer j'en ai fait une avec les complexes . Ca marche bien , ce n'est pas compliqué , mais ça n'explique rien du tout 
On note 0 ,1 , r les affixes des points A, B , C et d , e , f , g , h , i ceux des points D , E , F , G , H , I . Quelques calculs élémentaires nous donnent :
2(k−j)=(r−1)d+f−rh+1−r
2(l−k)=−rd+(r−1)f+h+r
2(j−l)=d−rf+(r−1)h−1
Comme r2=r−1 , les trois côtés du triangle JKL sont égaux .
Vasimolo
PS : j'ai réussi à réduire le problème initial mais je n'ai pas de réponse à cette réduction évitant les complexes ou les coordonnées , à suivre ...
#13 - 14-01-2018 13:44:06
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Un tas de tringles équilatéraux + INDICE
@Vasimolo : TB, golgot59 a utilisé le même outil que toi. Tu me diras quand je pourrai lâcher l'indice, il faut bien faire avancer le schmilblick...
#14 - 14-01-2018 18:09:14
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
un tas de triangkes équilatéraux + indice
Le week-end se termine et j'aurai peu de temps libre la semaine prochaine , il me semble que tu peux donner un indice 
Vasimolo
#15 - 14-01-2018 19:12:06
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
un tas de triangmes équilatéraux + indice
OK, c'est parti 
Voici un premier indice pour donner l'outil à utiliser. Si ça ne suffit pas, j'en donnerai un deuxième dans deux jours.
#16 - 14-01-2018 19:52:09
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,037E+3
Un tas de triangles équilatéraux + INDIE
Bonsoir,
une petite réponse vectorielle assez simple...
En partant des milieux du triangle équilatéral du centre, pour arriver au sommets du triangle pointillé bleu, par construction du milieu, j'obtiens la demi-somme des vecteurs représentés.
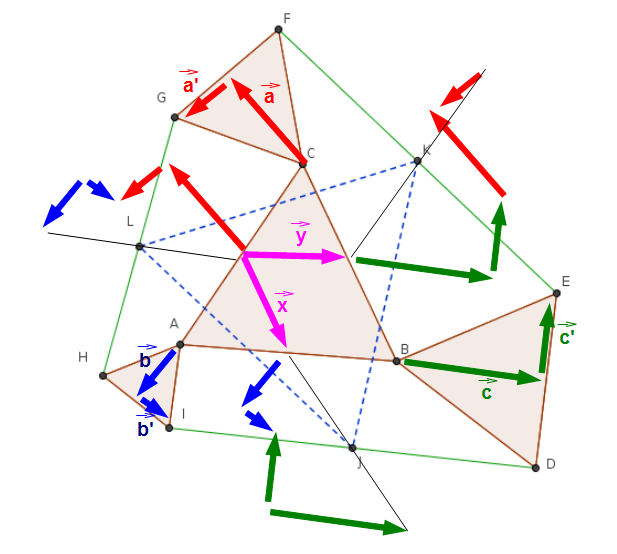
Pour aller de L à J , on effectue (sans m'embêter avec les flèches vectorielles, mais tout est orienté) :
( b' - b - a' - a ) / 2 puis x puis ( b + b' + c - c') / 2
Ce qui équivaut à : ( 2b' - a - a' + c - c ' ) / 2 +x
Pour aller de L à K, on effectue :
( b' - b - a' - a ) / 2 puis y puis ( c + c' + a - a' ) / 2
Ce qui équivaut à : ( c + c' - b + b' - 2a' ) / 2 + y
Maintenant, si par hasard on essayait d'opérer une petite rotation de 60° des premiers déplacements dans le sens trigo :
On a : ( 2b' - a - a' + c + c ' ) / 2 +x
C'est assez simple dans chaque triangle équilatéral :
Par rotation, x devient y, ( -a - a' ) devient ( -2a' ) et ( c - c' ) devient ( c+ c' ) et ( 2b' ) devient ( b' - b )
Après rotation ( 2b' - a - a' + c - c ' ) / 2 +x devient ( c + c' - b + b' - 2a' ) / 2 + y
Les deux déplacements sont identiques par une rotaion de 60° , on a un triangle équilatéral.
#17 - 14-01-2018 20:43:04
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Un tas de triangles équilatéraux + INDIC
@gwen27 : tout à fait, bravo 
C'est le principe de ma démonstration. Il y a moyen de la présenter encore plus simplement en choisissant d'autres vecteurs, mais l'essentiel est là.
#18 - 14-01-2018 21:28:11
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,037E+3
un tas fe triangles équilatéraux + indice
Oups, effectivement, j'aurais pris les côtés des triangles, ça aurait été plus simple...
#19 - 14-01-2018 21:42:40
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Un tas de tringles équilatéraux + INDICE
Oui 
#20 - 15-01-2018 11:01:21
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Un tas de triangles équilatéraux + INDCE
C'est marrant j'avais essayé plein de combinaisons avec Chasles sans aucun succès .
2.→LK=→LG+→GF+→FK+→LH+→HA+→AB+→BE+→EK2.→LK=→GF+→HA+→AB+→BE
On note R la rotation vectorielle d'angle 60° dans le sens direct :
R(2.→LK)=→CF+→IA+→AC+→DE=→IF+→DER(2.→LK)=(→IF+→DE)+(→JI+→JD)+(→EK+→FK)R(2.→LK)=(→JI+→IF+→FK)+(→JD+→DE+→EK)=2.→JK
Et JKL est équilatéral .
Vasimolo
#21 - 15-01-2018 11:07:14
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Un tas de trianglse équilatéraux + INDICE
@Vasimolo : bravo  Son regard sévère aura su te motiver... Son regard sévère aura su te motiver...
#22 - 17-01-2018 18:59:40
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
un tas de yriangles équilatéraux + indice
C'est terminé, merci aux courageux participants. Je vous livre ma façon de voir les choses, très proche de la méthode de Vasimolo.
On commence par démontrer à l'aide de la relation de Chasles (je passe les détails) que →LK s'écrit comme la moitié d'une somme de 4 vecteurs, chacun porté par un côté d'un des 4 triangles équilatéraux :
→LK=12(→HA+→AB+→BE+→GF)
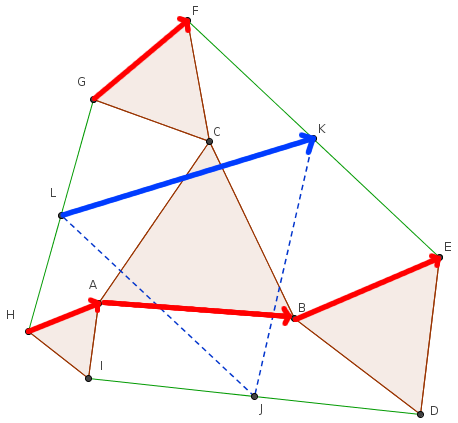
De même, on peut écrire :
→LJ=12(→GC+→CB+→BD+→HI)
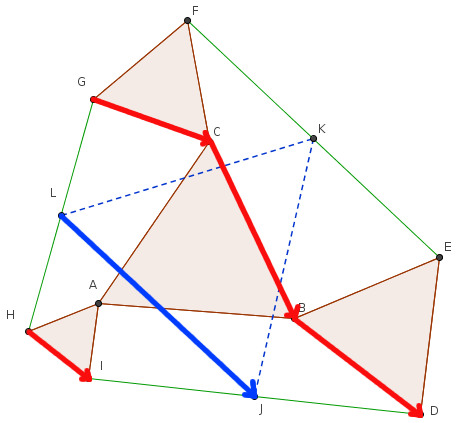
Les 4 triangles de départ sont équilatéraux, donc →GC, →CB, →BD et →HI sont les images de respectivement →GF, →AB, →BE et →HA par une rotation d'angle 60° dans le sens indirect.
On en déduit que →LJ est l'image de →LK par une rotation d'angle 60°, le triangle JKL est donc équilatéral.
#23 - 17-01-2018 22:08:13
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
un tas de ttiangles équilatéraux + indice
C'est clair , mais il faut avoir un œil d'aigle pour voir que la somme des rouges vaut deux bleus 
Bravo à toi !!!
Vasimolo
#24 - 18-01-2018 00:13:59
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
Un tas de triangles équilatéraux INDICE
Ohhhh !
Très joli, et effectivement assez simple une fois qu'on l'a vu ! 
(Mais pas sûr que mes secondes suivraient tous le raisonnement...)
Magnifique ! 
#25 - 18-01-2018 19:41:49
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Un tas de trriangles équilatéraux + INDICE
Il faut dire que j'ai eu de la réussite de tomber sur cette démo, je bricolais avec les vecteurs un peu au hasard quand j'ai eu l'illumination. C'est le genre de truc impossible à voir, mais qui éclaire merveilleusement le problème.
J'ai un peu peur que le gâteau 149 soit du même tonneau, d'y passer des semaines avant que n'émerge une démo élémentaire, mais bon, c'est le jeu, c'est un peu à cette drogue que l'on fonctionne 
|
 |

 Accueil
Accueil
 Forum
Forum













