 |
#1 - 12-02-2011 01:17:35
- SaintPierre
- Banni
- Enigmes résolues : 42
- Messages : 2063
- Lieu: Annecy
un peu de physiquz...
Deux balles sont placées au point A à une hauteur h du plan horizontal BC. La 1ère balle roule sur la surface inclinée AC, la seconde tombe librement suivant la verticale AB.
La balle qui roule se déplace avec une vitesse de ... % inférieure/supérieure à celle de la balle qui tombe en chute libre.
La question est de remplacer les pointillés par une valeur numérique et de choisir entre inférieure et supérieure.
Comme dans beaucoup de problèmes de ce type, on néglige les frottements.
C'est à l'intelligence d'achever l'oeuvre de l'intuition.
#2 - 12-02-2011 02:33:39
- L00ping007
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 2010
- Lieu: Paris
ub peu de physique...
On suppose aucun frottement dans l'air, et que la bille roule et ne glisse pas sur le plan.
Chute libre axe Bz orienté verticalement vers le haut
a=-g (pesanteur seule force)
v=-gt
z=−12gt2+h
On cherche t tel que z=0 : t=√2hg
Donc la vitesse vaut en B : v1=√2hg
Roulement plan incliné
Je choisis pour axes : (AC) axe des x (orienté de A vers C), et l'axe y orthogonal au plan incliné (vers le haut). Mon repère est donc (A,Ax,Ay)
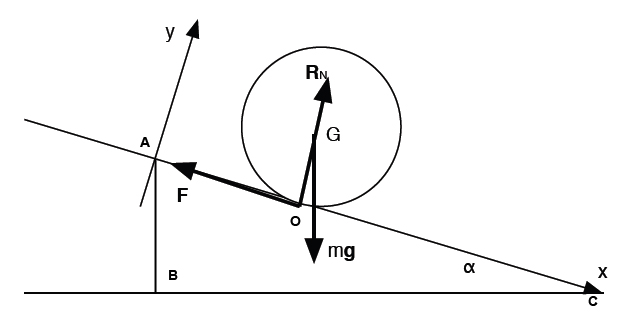
Raisonnons de manière énergétique
m masse de la bille, x,˙x,¨x les position,vitesse,accélération du centre de la bille.
Ep=mgx.sin(α)[/latex](lepoidsestlaseuleforcequitravaille)[latex]Ec=12m˙x2+12IGω2
où ω vitesse angulaire de rotation de la bille
et IG est le moment d'inertie de la boule par rapport à son axe de rotation.
Ca peut se calculer, sinon on cherche et on trouve : IG=25mR2 avec R rayon de la bille
En dérivant l'énergie mécanique (énergie potentielle + énergie cinétique), qui doit être constante :
0=ddt(12m˙x2+1225mR2ω2−mgx.sin(α))
donc 0=m˙x¨x+25mR2˙ωω−mg˙xsin(α)
La condition de non glissement est : ˙x=−Rω (vitesse nulle au point de contact O), donc on peut diviser par ˙x (cas pas très intéressant ...) et par m :
0=¨x+25¨x−gsin(α)
et finalement 75¨x=gsin(α)
75˙x=gsin(α)t
75x=12gsin(α)t2
On cherche t tel que x vaut hsin(α)
t=√14h5g1sin(α)
A cet instant, la vitesse vaut :
v2=√57√2hg
On voit donc que le rapport des 2 vitesses vaut r=v2v1=√57
La bille sur le plan incliné a une vitesse qui vaut 84,5% de celle de la bille en chute libre.
La billle sur le plan incliné a donc une vitesse 15,5% inférieure à celle de la bille en chute libre
L'astuce est de ne pas considérer la boule comme un point matériel, du coup ça introduit le moment d'inertie et le rapport 25
#3 - 12-02-2011 02:47:38
- mitsuidewi
- Professionnel de Prise2Tete
- Enigmes résolues : 49
- Messages : 250
- Lieu: dans une chambre universitaire
Un peu d physique...
Euh, sauf faute de ma part. Tu es sûr qu'avec ton énoncé actuel on peut répondre à la question ?
On a pas l'angle que fait AC avec BC, on ne sait pas si les balles ont une vitesse initiales.
#4 - 12-02-2011 02:57:41
- mitsuidewi
- Professionnel de Prise2Tete
- Enigmes résolues : 49
- Messages : 250
- Lieu: dans une chambre universitaire
Un peu de phsique...
Et puis la balle en chute libre accélère jusqu'à une vitesse limite dépendant du coefficient de frottement avec l'air. Bref pour moi c'est énigme est utopique sans les informations nécessaires.
#5 - 12-02-2011 06:22:42
- halloduda
- Professionnel de Prise2Tete
- Enigmes résolues : 24
- Messages : 495
- Lieu: Ardèche
Un peu de physiuqe...
La balle qui tombe subit l'accélération g.
Celle qui roule subit une accélération g∗sin^ACB, répartie entre la descente et la rotation.
Elle va donc aller moins vite que si elle glissait.
Car elle transforme l'énergie potentielle à la fois en énergie cinétique de translation et en énergie cinétique de rotation, les deux étant liées par la condition de non-glissement v=R∗ω (où ω=vitesse angulaire)
Au bout du temps t, sa vitesse v est telle que :
\frac 1 2 *(m*v^2+I\omega^2)= m*g*h = m*g*l*sin{\hat {ACB}}[/latex], où [latex]v=\frac {dl} {dt}[/latex], m représente la masse, et [latex]I=\frac {2*m*R^2} 5[/latex] moment d'inertie de rotation d'une sphère pleine. [latex]\frac 7 {10}*v^2=\frac 7 {10}*\gamma^2*t^2=\frac 1 2 *g*\gamma*t^2*sin{\hat {ACB}
Accélération \gamma={\frac 5 7}*g*sin{\hat {ACB}}, et par intégration :
v=\gamma*t=\frac 5 7 *sin{\hat {ACB}} fois celle de la balle qui tombe, qui vaut g*t.
#6 - 12-02-2011 09:24:46
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3523
- Lieu: 94110
n peu de physique...
Si il s'agit bien d'une balle (creuse) et non d'une boule (pleine), la réponse n'est pas la même mais elle dépend encore de l'épaisseur de la paroi. A moins que l'on suppose que la masse soit entièrement répartie à la surface de la balle (épaisseur de paroi tendant vers 0) ...
#7 - 12-02-2011 09:30:18
- irmo322
- Professionnel de Prise2Tete
- Enigmes résolues : 36
- Messages : 203
Un peu de phsyique...
Soit alpha l'angle de AC par rapport à l'horizontal.
Si on néglige les forces de frottement, la balle roulant sur la surface inclinée AC subit une accélération égale à cos(alpha).P, où P est le poids s'appliquant à la balle.
Donc la balle qui roule se déplace avec une vitesse de 100(1-cos(alpha)) % inférieure à celle de la balle qui tombe en chute libre.
Edit:
Faut pas t'arrêter là St-Pierre... Qu'est-ce qui ne va pas dans nos réponses?
#8 - 12-02-2011 10:27:49
- franck9525
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1935
- Lieu: 86310
Un peu de phsyique...
La vitesse de la balle sur le plan inclinée est égale à celle de la balle en chute libre affecté d'un coefficient égal au sinus de la pente du plan incliné. La balle qui roule se déplace avec une vitesse de (1-sin\alpha) % inférieure à celle de la balle qui tombe en chute libre.
exemple:
un plan à 20% a une pente de 11,3º. Après une seconde, la balle en chute libre a une vitesse de 9.81 m/s, cette vitesse est verticale. La balle qui roule une vitesse de sin(11,3)*10=1.96m/s sur le plan incliné; cette vitesse est (1-sin(11.3))=80% inférieure à celle qui tombe librement.
Pour une pente à 100%, la vitesse de la balle qui roule serait 29% inférieure a celle de la balle qui chute.
The proof of the pudding is in the eating.
#9 - 12-02-2011 10:55:04
- SaintPierre
- Banni
- Enigmes résolues : 42
- Messages : 2063
- Lieu: Annecy
Un eu de physique...
Grand bravo à L00ping, qui est le seul à avoir répondu parfaitement à la question !
Bon samedi.
C'est à l'intelligence d'achever l'oeuvre de l'intuition.
#10 - 12-02-2011 11:50:14
- mitsuidewi
- Professionnel de Prise2Tete
- Enigmes résolues : 49
- Messages : 250
- Lieu: dans une chambre universitaire
un peu de physiqie...
Donc c'est faisable ?
etrange...
#11 - 12-02-2011 15:15:10
- fix33
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1198
- Lieu: Devant un clavier depuis 1748
Un peu de phyysique...
Il faudrait savoir si la surface inclinée AC opère des frottements sur la balle !
De même la chute libre signifie-t-elle sans frottement ??
Je ne vien sur se site que pour faire croir que je suis treise intélligens.
#12 - 12-02-2011 16:37:41
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3523
- Lieu: 94110
Un peu de physiqque...
Essayons de rassembler mes vieux souvenirs ...
Soient Vcl la vitesse de la balle en chute libre, Vr la vitesse de la balle qui roule, R le rayon de la balle, m sa masse, I son moment d'inertie, w sa vitesse de rotation.
Au bout d'un certain temps, l'énergie potentielle W = m*g*h de la balle se sera transformée en énergie cinétique :
Wcl = 1/2 *(m*Vcl²) pour la balle en chutte libre
et Wr = 1/2 *(m*Vr² + I*w²) pour la balle sur le plan inclinée.
(à condition bien sûr, que l'on néglige le coëfficient de résistance au roulement et le frottement visqueux de l'air, d'une part, et, d'autre part que l'angle du plan incliné soit inférieur à l'angle d'adhérence balle/plan.)
Avec I = 2/3 (m*R²) et w = Vr/R on obtient :
Wr = 1/2 *m*(Vr² + 2/3 *Vr²)
Donc Vcl² = 5/3 * Vr² et Vr = sqrt{3/5}*Vcl
Sauf erreur de ma part, la vitesse de la balle qui roule sera donc 22.54 % inférieure à celle de la balle en chutte libre.
Remarque : Avec une shère pleine, le terme 2/3 devient 2/5 et la vitesse de la balle qui roule sera 15.48 % inférieure à celle de la balle en chutte libre.
Avec une balle d'épaisseur non nulle, la valeur recherchée sera intermédiaire entre ces 2 valeurs.
#13 - 12-02-2011 17:05:00
- rivas
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1106
- Lieu: Jacou
Un peu de physiqu...
Sans tenir compte des forces de frottements sur le plan incliné ni dans l'air puisqu'on n'a aucune information permettant de le faire (volume de la balle, matière, poids, ...), on néglige les forces de frottements.
Dans ce cas la conservation de l'énergie le long du trajet donne:
Ec+Ep=constante.
Ec, l'énergie cinétique est nulle en A dans les 2 cas et vaut 1/2mv^2 à l'arrivée sur le plan BC. v peut être différent dans chaque cas pour le moment.
L'énergie potentielle est choisie pour valoir 0 sur le plan BC. Elle vaut donc mgh en A dans les 2 cas. On voit donc que dans les 2 cas, l'énergie cinétique est la même sur le plan BC: mgh. Donc la vitesse de la balle, vitesse linéaire le long de sa trajectoire, est la même en arrivant en BC (et tout le long du trajet en fait).
La vitesse verticale par contre n'est pas la même (à un sin(t) près).
Merci pour un peu de physique 
#14 - 12-02-2011 20:13:29
- vitox
- Amateur de Prise2Tete
- Enigmes résolues : 7
- Messages : 2
Un eu de physique...
264 m, valeur bien supérieure à 62,5 m calculée en 1. Il faut prendre en compte la résistance de l'air. Le modèle de la chute libre n'est pas correct. 
#15 - 12-02-2011 21:03:05
- LeSingeMalicieux
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1298
- Lieu: Haute-Marne
Un peu de physsique...
J'ai très envie de m'y coller 
Mais, au juste, quelle est la question ?
Calculer le rapport entre les vitesses des deux balles ? Déterminer quelle vitesse est supérieure à l'autre ? Ou trouver un piège ?
Question bonus : doit-on tenir compte de quelconques forces de frottement ?
Avoir quatre mains, c'est plus pratique pour taper sur un clavier.
#16 - 13-02-2011 07:37:28
- mitsuidewi
- Professionnel de Prise2Tete
- Enigmes résolues : 49
- Messages : 250
- Lieu: dans une chambre universitaire
un pzu de physique...
Au fait un plan comporte au moins 3 points. Je sais je suis chiant. Mais il est tellement bizarre cet énoncé.
J'attends la réponse avec impatience !
#17 - 14-02-2011 19:23:11
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3230
- Lieu: Luxembourg
Un peu de physique..
Bonjour,
Je tente une réponse qui me semble pourtant trop simpliste: s'il n'y a pas de frottement et peu importe leur masse, les deux balles arrivent en même temps.
Donc la balle qui roule se déplace avec une vitesse supérieure à celle de la balle qui tombe en chute libre de 100 x (AC/AB - 1) %, soit 100 x (1/sinA - 1) %, A étant l'angle entre la trajectoire de la balle qui roule avec l'horizontale.
Bonne soirée.
Frank
#18 - 14-02-2011 19:49:22
- SaintPierre
- Banni
- Enigmes résolues : 42
- Messages : 2063
- Lieu: Annecy
Un peu de pyhsique...
Pas besoin de connaître la valeur de l'angle A. 
C'est à l'intelligence d'achever l'oeuvre de l'intuition.
#19 - 14-02-2011 23:18:27
- shadock
- Elite de Prise2Tete
- Enigmes résolues : 39
- Messages : 3334
un peu dr physique...
Sans y avoir réfléchit, à première vue la balle qui roule va un pourcentage moins vite, mais si on concidère qu'il n'y a que le poids qui travaille, alors la balle arrive à la même vitesse en bas, car d'après de Th. de l'énergie cinétique :
\sum W(\vec{F_{ext}}) = \Delta E_c[/latex] d'où [latex]mgh=\Delta E_c
et en simplifiant on obtient :
V_f=\sqrt{2gh}
Si on se fait un petit dessin :
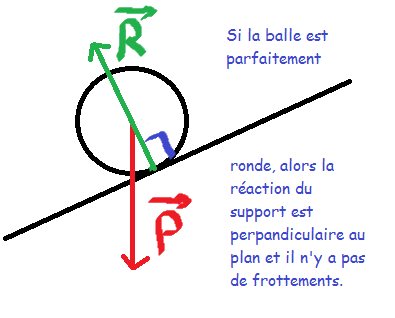
Je pense que je me suis planté, mais pour moi dans ce cas, les balles vont à la même vitesse.
Shadock 
"L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
#20 - 16-02-2011 10:23:49
- halloduda
- Professionnel de Prise2Tete
- Enigmes résolues : 24
- Messages : 495
- Lieu: Ardèche
Un peu de pphysique...
Si on compare les vitesses de passage à hauteur donnée, Gazole a évidemment raison.
Mais ces vitesses ne seront pas atteintes à un même instant.
L'énoncé laisse entendre que la comparaison porte sur les vitesses à un même instant.
Il est évident que l'angle A intervient, pour s'en convaincre, mettez-le à 89° et attendez !
Vous vous êtes tous plantés, même l'auteur, ou alors il a mal rédigé l'énoncé.
Il aurait dû dire "vitesses à l'arrivée en bas" au lieu de "se déplace avec une vitesse".
#21 - 16-02-2011 10:44:08
- irmo322
- Professionnel de Prise2Tete
- Enigmes résolues : 36
- Messages : 203
Un peu dde physique...
C'est clair que l'énoncé était plus que imprécis.
Il manquait pas mal de choses:
- le fait que l'on prenne les vitesses en bas et pas à un instant donné,
- la balle est-elle pleine ou creuse,
- le fait que les frottements sont négligés sauf ceux qui font rouler la balle (si on néglige tous les frottements alors la balle glisse, c'est ce que beaucoup ont considéré).
#22 - 16-02-2011 11:01:06
- gasole
- Elite de Prise2Tete
- Enigmes résolues : 40
- Messages : 1117
- Lieu: Toulouse
Un peu d ephysique...
Je ne m'y suis pas mis sur celui-là,
- d'une part parce que l'énoncé était pas clair (il fallait deviner qu'on parlait des vitesses en bout de course), ça n'est plus de la physique mais de la psychologie ("trouver la logique de SaintPierre)
- et d'autre part, je trouve que Saint-Pierre n'assure pas beaucoup le SAV (sans doute occupé à autre chose j'imagine)... pas très cool
#23 - 16-02-2011 12:01:06
- kosmogol
- Banni
- Enigmes résolues : 49
- Messages : 11,928E+3
UUn peu de physique...
http://enigmusique.blogspot.com/
#24 - 16-02-2011 12:29:41
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3523
- Lieu: 94110
Un ppeu de physique...
Je suis d'accord pour dire avec gazole que l'énoncé n'était pas très clair et qu'il fallait d'abord faire preuve de logique pour deviner quelle pouvait être la seule question complète raisonnable. Mais, à mon humble avis, cela ne fait que rajouter du sel à la résolution d'une énigme.
Un peu d'accord aussi pour dire que SaintPierre n'assure pas toujours un suivi régulier...
Alors, je vais essayer d'y remédier.
Je constate que :
- pour que le problème ait un sens, il fallait le compléter par : vitesse ... au moment où le centre de gravité de la balle passe par le plan horizontal dont la trace sur le plan vertical des chutes est BC.
- LOOping et halloduda, les seuls à avoir envisagé le moment d'inertie, parlent et utilisent celui d'une boule pleine et non d'une balle (en général, creuse).
- je trouve exactement le même résultat que LOOping (-15.48 %) dans le cas qu'il a considéré.
- que c'était un bon problème (avec les réserves déjà citées) pas du tout insoluble puisque certains y sont arrivés. Merci SaintPierre.
#25 - 16-02-2011 12:43:05
- mitsuidewi
- Professionnel de Prise2Tete
- Enigmes résolues : 49
- Messages : 250
- Lieu: dans une chambre universitaire
un peu de phyqique...
Vous êtes du genre chipoteur les gars !
Mais je suis entièrement d'accord avec vous.
Cependant d'autres personnes ont trouvé, donc la vérité est qu'on a pas assez réfléchis sur cette énigme, car malgré l'énoncé incomplet, plusieurs ont trouvé la bonne réponse.
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum








