Enigme C'est peu impair, père ! @ Prise2Tete

nodgim · #1

Bonsoir à tous,
Je sais que vous êtes déja bien occupés avec la nouvelle énigme d'Ebichu, alors je vais vous laisser du temps pour ce problème simple ou pas simple, c'est selon...

Parmi les 2015 nombres C(2016,1) à C(2016,2015), combien y en a t'il d'impairs ?

Je rappelle que C(2016,n) est le nombre de combinaisons de n éléments parmi 2016.

Bon amusement

PS: vous n'êtes pas obligé d'utiliser ces logiciels surpuissants qu'on trouve sur le net. C'est même recommandé de les oublier.

enigmatus · #2

Bonsoir,
Sauf erreur, la réponse est 62.

PS: vous n'êtes pas obligé d'utiliser ces logiciels surpuissants qu'on trouve sur le net.

Donc ce n'est pas interdit… Et je n'ai d'ailleurs utilisé que ça :

Code:

#!/usr/bin/env python

N=2016
impair=0; r=1
for n in range(1,N):
   r=r*(N-n+1)//n
   impair+=r%2

print('%5d %5d'%(N,impair))

Ebichu · #3

Comme je suis le seul à ne pas être trop occupé par ma nouvelle énigme, je tente ma chance...

Dans le triangle de Pascal, le nombre de nombres impairs sur la ligne numéro n (celle qui contient les C(n,k)) est égal à 2^i, où "i" est le nombre de 1 dans l'écriture de n en binaire.

Pour démontrer ça, on trace le triangle de Pascal en remplaçant les nombres par 1 quand ils sont impairs, et par 0 quand ils sont pairs. On remarque alors que le triangle contenant les lignes 0 à 2^j-1 est un assemblage de trois triangles égaux à celui contenant les lignes 0 à 2^(j-1)-1, et d'un triangle inversé rempli de 0. Le résultat s'en déduit par récurrence sur j.

Pour le problème qui nous intéresse, on remarque que 2016 vaut 11111100000 en binaire, est la réponse vaut donc 2^6-2 = 62 (on enlève 2 car C(2016,0) et C(2016,2016) ne comptent pas).

nodgim · #4

@Enigmatus: oui, ça corrobore ce qu'on obtient en réfléchissant un peu. Mais franchement tu loupes quelque chose à ne pas tenter à la main.

@Ebichu: c'est la bonne réponse, mais pourquoi ne suis pas surpris ?
Bravo à toi.
Et si je te demandais où se trouvent ces impairs ?

nodgim · #5

Halloduda, as tu bien compris la question ?

Vasimolo · #6

Salut Nodgim

Par curiosité j'ai jeté un coup d'oeil au triangle de Pascal en ne gardant que la parité des valeurs :

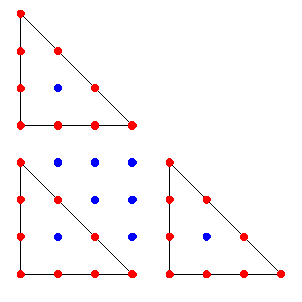
Les points rouges sont impairs et les bleus pairs .

On obtient un réseau de triangles rectangles-isocèles suivant toujours le même schéma c'est à dire que si on réduit chaque triangle à un point rouge on garde la même structure .

Après , le calcul du nombre de points rouges sur une ligne ne me passionne pas outre-mesure , sauf s'il y a une perle qui se cache en dessous

Vaimolo

Ebichu · #7

Si je me demande à quoi ressemble la ligne numéro 37=100101 dans le triangle de Pascal formé de zéros et de 1 : elle est formée de deux fois la ligne 00101=5 (j'ai fait sauter le 1 de gauche), et entre ces deux lignes 5, il faut rajouter (32-1)-5 = 26 zéros (32 étant la valeur décimale du 1 que j'ai fait sauter).

La ligne 5 étant "110011", on obtient pour la ligne 37 : "110011{26 zéros}110011", soit 38 bits.

Appliquons ce raisonnement avec 2016.

La ligne 2016=11111100000 est formée de deux lignes 1111100000=992, séparées par 1023-992=31 zéros.
La ligne 992=1111100000 est formée de deux lignes 111100000=480, séparées par 511-480=31 zéros.
Et ainsi de suite jusqu'à la ligne 32 qui est formée de deux lignes 0 (=un unique 1), séparées par 31 zéros.

La ligne 2016 est ainsi une alternance de 1 et de "31 fois 0" : il y a un nombre impair (C(2016,0)=1), puis 31 nombres pairs, puis un nombre impair, puis 31 nombres pairs... jusqu'à C(2016,2016)=1 qui est impair. Pour un total de 64 nombres impairs et 63*31=1953 nombres pairs, soit 64+1953=2017 nombres au total.

w9Lyl6n · #8

Considérons les puissances de 2 en facteur dans la suite des nombres du numérateur et du dénominateur de C(2016,n):

_ au dénominateur, n! : 0 1 0 2 0 1 0 4 0 1 ....
_ au numérateur 2016 = 32 * 63, la suite est la même en sens inverse et en commençant à 32.
On n'aura pas de surprise avec l'apparition de grande puissances de 2 dans le numérateur puisque 2016 est très proche de 2048 qui est une puissance de 2.

La suite du numérateur se déroule donc tranquillement comme si on commençait à 32 et dans le même sens.

Comme les nombres intermédiaires entre chaque puissance de 32 sont les mêmes pour chaque suite, on en déduit que tout les 32, les deux suites contiennent exactement les même nombres, C(2016, n) est alors impair.

il y a donc 62 impairs dans la liste pour n = 32, 64, ..., 61*32, 62 *32

Merci pour l'énigme

nodgim · #9

@Vasimolo: une perle, je sais pas, mais quelque chose de plus à creuser, oui c'est sûr ! En fait, le résultat est plutôt bluffant de simplicité....

@Ebichu et Matthieu: c'est bien ça, bravo.

BlaiseP · #10

Il y a 62 nombres impairs. Les 31 premiers, et les 31 derniers.

Explication :

Comme je suis fainéant, j'ai cherché sur le net le triangle de Pascal.
J'ai trouvé un article sympa https://mathinfo.unistra.fr/fileadmin/u … 1_9-22.pdf
qui explique plein de choses avec des belles démonstrations.
Le théorème 12, page 20, dit qu'il faut compter le nombre de 1
dans la représentation binaire de 2016 (11111100000).

"Théorème 12 :...
En particulier le nombre de coefficients impairs dans la ligne n est égal à 2^L(n) où L(n) est le nombre de chiffres 1 dans la représentation binaire de n."

Il y a 6 "1" dans la représentation binaire.. 2^6 = 64.
Mais il faut enlever C(2016,0) et C(2016,2016), tous deux impairs car égaux à 1.
On a donc 64-2=62 nombres impairs.

Pour trouver où sont ces nombres, j'ai pris une méthode brutale : un (gros) tableau Excel.
Remplir la première ligne avec FAUX(), et ensuite la première colonne avec VRAI(). Garnir le reste du tableau avec un XOR fait maison : =((A1+B1)=1)

Mais je ne suis pas du tout fier d'avoir fait comme cela, alors voila ce que je propose :
Les valeurs de C(2049,1) à C(2049;2048) sont toutes paires.
donc, les valeurs de C(2048, n) sont toutes impaires
Dans le triangle de Sierpiński, cela fait une ligne toute noire.
si on remonte de 32 cases, on se retrouve avec à gauche et à droite des triangles
dont la base fait 32 valeurs impaires, séparées par 32 valeurs paires situées au centre du triangle.
Bon, je ne suis pas très convaincu.

Vasimolo · #11

Si on veut détailler le décompte :

Le nombre de triangles est donné par 2^u où u est le nombre de 1 dans l’écriture binaire de l’entier n en excluant les deux derniers chiffres . Les 1 des deux derniers chiffres donnent le nombre de points p sur la ligne dans chaque triangle . Le nombre total de combinaisons impaires est donc 2^u avec u le nombre total de 1 dans l'ensemble de l'écriture binaire . En fait il faut enlever 2 au total car tu refuses de compter c_n^0 et c_n^n : I=2^u-2 .

Exemple : 2016=111110000 , I=2^5-2=30 .

Vasimolo

nodgim · #12

@Vasimolo: Il y a juste un problème de calcul de puissance à régler, et ce sera bon (2016 en binaire ?)
En fait, j'ai éludé les extrémités, car de parité évidente.

Vasimolo · #13

Oui , 2016=11111100000 donc I=2^6-2=62 , je suis nul en calcul

Il me semble quand même que le résultat est plus joli si on autorise les deux combinaisons extrêmes mais ce n'est que mon avis .

Vasimolo

masab · #14

Pour [latex]1\leq p\leq 2015[/latex], il y a exactement 62 combinaisons [latex]C_{2016}^p[/latex] impaires.

Ce sont les combinaisons [latex]C_{2016}^{32\,k}[/latex] avec k entier, [latex]1\leq k\leq 62[/latex].

Voici la preuve dans le pdf ci-joint :

Télécharger PDF

nodgim · #15

Beaucoup de bonnes réponses pour cette énigme qui était apparemment trop classique, semble t il. Ce qui peut arriver quand on trouve un résultat soi même sans s'informer si c'est connu ou pas....

En tout cas, bravo à tous ceux qui ont retrouvé ce résultat.

J'ai bâti mon raisonnement sur les puissances de 2 des entiers naturels, dont la suite peut s'écrire, en partant de 1:
0102 0103 0102 0104 0102 0103 0102 0105 .....
A partir d'une puissance comme 4 par exemple, on se rend compte qu'on lit la même chose vers la droite ou vers la gauche. Cette symétrie facilement démontrable permet de retrouver les impairs des combinaisons. Pour un nombre comme 29 par exemple, les combis successives sont:
29/1
(29/1)(28/2)
(29/1)(28/2)(27/3)
....
Traduit en puissance de 2:
0-0--->impair
(0+2)-(0+1)=1 pair
(0+2+0)-(0+1+0)=1 pair
(0+2+0+1)-(0+1+0+2)=0 impair
Du fait de la symétrie, une puissance p au numérateur ne peut être compensée que par une puissance p au dénominateur

On en arrive vite à écrire le nombre à analyser en base 2. Pour 2016:

11111100000 au numérateur et 1 au dénominateur pour C(2016,1)
Il faudra aller à 100000 au dénominateur pour compenser le ...00000 du num.

C (11111000000 ; 100000) est impair.

De proche en proche, on se rend compte qu'il faudra manipuler tous les 1 du nombre binaire pour arriver à C(n,n).

Donc de C(n,0) à C(n,n) il y a 2^i impairs, si i est le nombre de 1 dans l'écriture binaire de 1. Si on ôte les extrémités, c'est 2^i-2.

Forum dédié aux énigmes et à toutes formes de jeux de logique.	Déconnexion
Tu n'es pas identifié sur Prise2tete : s'identifier. Accueil Forum	[+]

#1 - 17-02-2016 20:04:41

c'est peu ompair, père !

#0 Pub

#2 - 17-02-2016 22:22:58

C'eest peu impair, père !

Code:

#3 - 17-02-2016 23:09:51

C'est pu impair, père !

#4 - 18-02-2016 08:46:47

'Cest peu impair, père !

#5 - 18-02-2016 11:31:55

C'est pu impair, père !

#6 - 18-02-2016 11:45:49

C'st peu impair, père !

#7 - 18-02-2016 11:46:31

C''est peu impair, père !

#8 - 18-02-2016 16:01:10

C'est peu impair ,père !

#9 - 18-02-2016 16:47:15

c'est peu umpair, père !

#10 - 18-02-2016 23:06:26

C'est pu impair, père !

#11 - 19-02-2016 09:25:01

c'est peu impair, pèrr !

#12 - 19-02-2016 10:07:01

c'est pzu impair, père !

#13 - 19-02-2016 10:17:51

C'est peu impair, pre !

#14 - 19-02-2016 11:12:56

C'est ppeu impair, père !

#15 - 25-02-2016 08:57:45

C'est peu impair, pèrre !

Réponse rapide

Sujets similaires

Mots clés des moteurs de recherche

Pied de page des forums