 |
#1 - 09-03-2011 18:03:03
- SaintPierre
- Banni
- Enigmes résolues : 42
- Messages : 2063
- Lieu: Annecy
22, v'la les poluies !
Dans la figure ci-dessous, il y a deux poulies, l'une de rayon 3 cm, l'autre de rayon 2 cm. Les centres des poulies sont distants de 6 cm.
Quelle est la longueur totale du câble autour des deux poulies ?

C'est à l'intelligence d'achever l'oeuvre de l'intuition.
#2 - 09-03-2011 18:07:40
- MthS-MlndN
- Hors d'u-Sage
- Enigmes résolues : 49
- Messages : 12,414E+3
- Lieu: Rouen
22, v'la le spoulies !
Enfin de la géométrie facile !
Deux demi-cercles de rayons respectifs 2 et 3 cm, plus deux hypoténuses de triangles rectangles de côtés de l'angle droit 1 et 6 cm.
Ca nous donne [latex]5 \pi + 2 \sqrt{37}[/latex], soit environ 27,87 cm.
Podcasts Modern Zeuhl : http://radio-r2r.fr/?p=298
#3 - 09-03-2011 18:24:35
- L00ping007
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 2010
- Lieu: Paris
22, v'ka les poulies !
La longueur du câble peut être découpé en 3 parties :
- la partie en contact avec la grande poulie : demi-périmètre de la grande poulie = [latex]\pi R[/latex]
- la partie en contact avec la petite poulie : demi-périmètre de la petite poulie = [latex]\pi r[/latex]
- 2 fois la distance entre les 2 points les plus "hauts" des 2 poulies.
Calculons cette dernière distance x.
Un petit coup de Pythagore nous donne :
[TeX]x^2=d^2+(R-r)^2[/TeX]
Et au final : [latex]L=\pi(R+r)+2\sqrt{(R-r)^2+d^2}[/latex]
Application numérique : L=27,87cm
#4 - 09-03-2011 18:26:34
- halloduda
- Professionnel de Prise2Tete
- Enigmes résolues : 24
- Messages : 495
- Lieu: Ardèche
22, v'la les piulies !
Si on pose [latex]\alpha=\arcsin \frac 1 6[/latex]
[TeX]L=5*\pi+2\alpha+12\cos \alpha \approx 27.8750 cm[/TeX]
#5 - 09-03-2011 18:30:51
- SaintPierre
- Banni
- Enigmes résolues : 42
- Messages : 2063
- Lieu: Annecy
22, v'la les pouloes !
Les problèmes trop difficiles amènent trop peu de réponses.
3 bonnes réponses !
C'est à l'intelligence d'achever l'oeuvre de l'intuition.
#6 - 09-03-2011 18:44:23
- langelotdulac
- Ange de Prise2Tete
- Enigmes résolues : 49
- Messages : 2963
- Lieu: Paradis
22, v'la les poumies !
Tu es largement assez dingo pour qu'un Minito te semble cohérent \o/ !
#7 - 09-03-2011 18:49:46
- thedoums
- Professionnel de Prise2Tete
- Enigmes résolues : 23
- Messages : 223
#8 - 09-03-2011 19:07:15
- SHTF47
- Imprnnçbl de Prs2Tt
- Enigmes résolues : 39
- Messages : 1629
- Lieu: Autre nom du colin
22, v'la les poulies !!
Appelons L la longueur totale du câble. On sait que le câble forme un demi-cercle sur chaque poulie, de longueurs respectives 3π et 2π. Reste à trouver la longueur de câble tendu entre les poulies. Par symétrie, on voit que le segment supérieur est identique au segment inférieur.
Soient : A le centre de la poulie de gauche, B où le câble quitte cette poulie en haut, C où le câble quitte la poulie de droite en haut, et D le centre de cette poulie. Soit E le point du segment [AB] tel que (CE)//(AD).
De toute évidence, on a (AB)//(CD) et (EC) perpendiculaire à (AB). De plus, on remarque que EC=AD=6, et que le triangle BEC en E. D'après le théorème de Pythagore, on a :
BC²=BE²+EC², soit : BC=√(BE²+EC²) Or BE=BA-EA=1 car BE=3 et EA=CD=2
D'où: BC=√(1²+6²)=√37
Le cable a pour longueur L=3π+2π+2√37
Conclusion: L=5π+2√37
La musique est une mathématique sonore, la mathématique une musique silencieuse. [Edouard HERRIOT]
#9 - 09-03-2011 21:31:59
22, v'al les poulies !
bonjour,
R= 3
r = 2
d = 6
L = 2(R.acos(-(R-r)/d))+r.acos((R-r)/d)+√(d²-r²))
L ≈ 27,875018992587576938554422711608
JJ.
#10 - 09-03-2011 22:03:52
- SaintPierre
- Banni
- Enigmes résolues : 42
- Messages : 2063
- Lieu: Annecy
22, v'la les poulies
Excellentes réponses !
Euh... l'Angelote, ta réponse, c'est quoi au juste ? 
C'est à l'intelligence d'achever l'oeuvre de l'intuition.
#11 - 09-03-2011 22:33:28
- fix33
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1198
- Lieu: Devant un clavier depuis 1748
22, v'la les ooulies !
On pourrait dire que c'est la somme des 2 demi-cercles + 2 fois le côté bancale du trapèze...
Mais le côté bancale n'est pas tangent aux cercles exactement en leur axe y...
Bonne nuit !
Je ne vien sur se site que pour faire croir que je suis treise intélligens.
#12 - 09-03-2011 22:38:57
- looozer
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 697
- Lieu: Belgique
22 v'la les poulies !
Je trouve [latex]2 \sqrt{35}+5 \pi +\text{ArcTan}\left[\frac{\sqrt{35}}{17}\right]=27.54...[/latex]
Erreur! Je laisse le calcul mais je change la réponse : 27.875...
#13 - 09-03-2011 22:41:38
- SaintPierre
- Banni
- Enigmes résolues : 42
- Messages : 2063
- Lieu: Annecy
22, v'la les poulis !
looozer, ton résultat est proche, mais ce n'est pas la réponse attendue. 
C'est à l'intelligence d'achever l'oeuvre de l'intuition.
#14 - 09-03-2011 22:44:43
- JACK971
- Amateur de Prise2Tete
- Enigmes résolues : 31
- Messages : 1
#15 - 09-03-2011 22:48:18
- SaintPierre
- Banni
- Enigmes résolues : 42
- Messages : 2063
- Lieu: Annecy
22, v'la les pouliees !
Non, JACK971. 
Bienvenue sur le forum !
C'est à l'intelligence d'achever l'oeuvre de l'intuition.
#16 - 10-03-2011 00:12:19
- franck9525
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1935
- Lieu: 86310
22, v'la les pouliies !
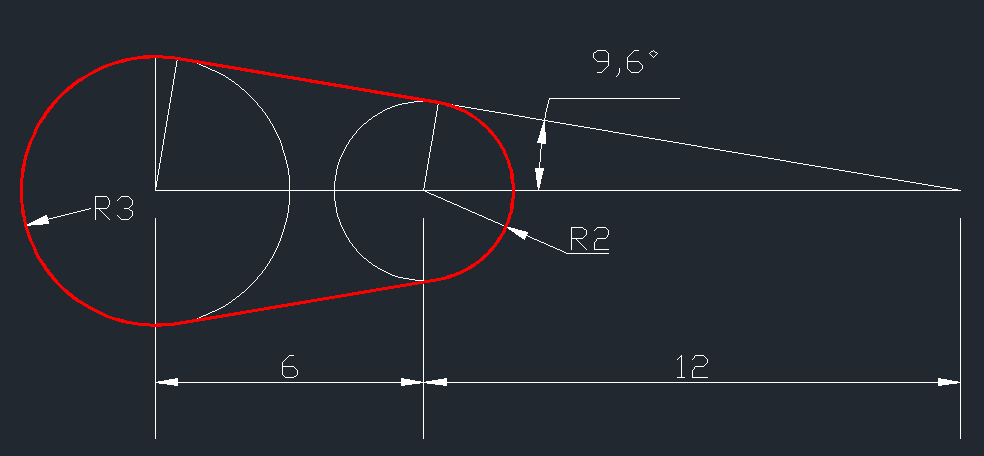
Soit [latex]T[/latex] la tangente aux cercles, [latex]L[/latex] la longueur du cable et [latex]\alpha[/latex] l'angle par rapport à la verticale,
[TeX]T=\frac{1}3\sqrt{(3\times6)^2-3^2}=\sqrt{35}[/TeX]
[TeX]\rm \alpha=arcsin(\frac{3}{18}) \approx 0.167 rad[/TeX][TeX]\rm L=(\pi+2\alpha)3+(\pi-2\alpha)2+2T \approx 27.875~cm[/TeX]
The proof of the pudding is in the eating.
#17 - 10-03-2011 00:37:01
- bd-42
- Amateur de Prise2Tete
- Enigmes résolues : 18
- Messages : 2
22, v'la lrs poulies !
On peut d'ores et déjà calculer facilement les deux demis-perimètres des cercles.
Il reste donc à calculer la longueur de cable qui ne touche pas la poulie.
Pour cela, on introduit un triangle rectangle, d'hypothénuse un de ces brins de cable", et les deux autres côtés étant donc de 6cm (distance entre les deux poulies) et de 1cm (=3-2). Le théorème de Pythagore nous donne alors que longueur d'un brin de cable=racine(1²+6²)=racine(37)
D'où
longueur totale=2*(longueur d'un brin de cable)+"demi-perimètre de la 1ère poulie"+"demi-perimètre de la 2nde poulie"
Soit:
longueur totale=2*racine(37)+3Pi+2Pi
longueur totale=2*racine(37)+5*Pi
Soit environ 28cm.
#18 - 10-03-2011 02:29:44
- chalibou
- Habitué de Prise2Tete
- Enigmes résolues : 25
- Messages : 16
22, v'la les pulies !
2*Racine(6²+0.5²) +2*2pi/2+3*2pi/2
=21,728760557345113932377337431587
#19 - 10-03-2011 08:11:27
- mitsuidewi
- Professionnel de Prise2Tete
- Enigmes résolues : 49
- Messages : 250
- Lieu: dans une chambre universitaire
22, v'la lse poulies !

Bon, visiblement la longueur du fil est égale à la moitié du périmètre de la première roue, plus la moitié du périmètre de la 2eme roue, plus 2 fois la longueur x vue sur le dessin.
L=3 pi + 2 pi + 2 racine (1+36)
= 5 pi + 2 racine(37)
#20 - 10-03-2011 08:45:33
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3222
- Lieu: Luxembourg
222, v'la les poulies !
Bonjour,
J'ai 4 tronçons de câbles que je vais rajouter:
1°) les 2 morceaux droits de même longueur
J'écris Pythagore dans le triangle rectangle formé par les 2 centres des poulies et l'intersection du grand rayon avec la parallèle à la chaîne:
x^2 + (3-2)^2 = (3+1+2)^2 donc x=V35 qu'on a 2 fois
2°) le morceau partiel autour de la grande poulie
y = 2pi R1 x (pi + 2a) / 2pi = 3 x (pi + 2a) avec a = arcsin (1/6) en radians
3°) le morceau partiel autour de la petite poulie
y = 2pi R2 x (pi - 2a) / 2pi = 2 x (pi - 2a) avec a = arcsin (1/6) en radians
Au final, on cherche L = 2x + y + z = V35 + 5pi + 2arcsin(1/6)
soit L = 27,875 environ.
Bonne journée.
Frank
#21 - 10-03-2011 15:29:28
- sofox
- Professionnel de Prise2Tete
- Enigmes résolues : 47
- Messages : 109
- Lieu: Besançon
22, v'la les pooulies !
longueur de courroie "autour" des poulies : la moitié de la circonférence, donc :
(2 x pi x R)/2, soit 9,425 cm pour la grande et 6,283 cm pour la petite.
longueur de courroie entre les poulies : c'est l'hypoténuse AC du triangle rectangle ABC, où AB= 6 cm et BC= la hauteur qui sépare le sommet des 2 poulies=1 cm.
AB^2 + BC^2= AC^2 <=> AC^2=37 <=> AC = 6,082 cm
on retrouve AC "en haut" et "en bas" entre les deux poulies, donc longueur de courroie totale = (6,082 x 2) + 9,425 + 6,283 = 27,872 cm
d'une part, j'espère ne pas m'être trompé  ; d'autre part, est-ce qu'une âme charitable pourrait m'expliquer comment on calcule une racine carrée avec cette %U#@!N de calculatrice windows svp ? ; d'autre part, est-ce qu'une âme charitable pourrait m'expliquer comment on calcule une racine carrée avec cette %U#@!N de calculatrice windows svp ?
Schizos Are Never Alone
#22 - 10-03-2011 17:07:19
- SaintPierre
- Banni
- Enigmes résolues : 42
- Messages : 2063
- Lieu: Annecy
22, v'la les pulies !
Bravo pour vos solutions. Mention spéciale à Franck pour la joliesse de la sienne.
C'est à l'intelligence d'achever l'oeuvre de l'intuition.
#23 - 11-03-2011 07:12:33
- NickoGecko
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1821
22, v'ma les poulies !
Bonjour !,
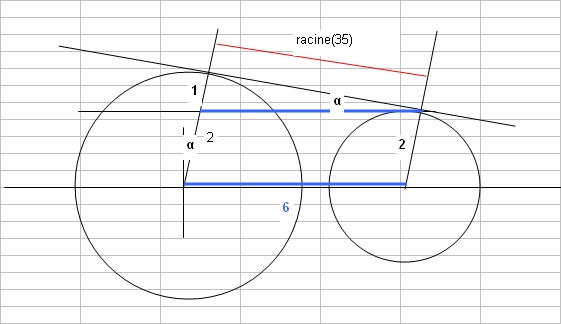
La longueur de la courroie est à décomposer selon
- la partie frottant sur la grande poulie de rayon 3 = (pi + 2 *alpha)*3
- les deux parties "tendues" rectilignes (haut +bas) = racine (35) * 2
- la partie frottant sur la petite poulie de rayon 2 = (pi - 2*alpha) * 2
On a alpha = arctg (1/6) au fait.
Application numérique : longueur totale = 27,87 cm
A comparer avec le cas ou l'on négligerait alpha (alpha = 0),
on trouverait : 27,54 cm, et une telle courroie serait trop courte !
Une petite généralisation :
R : rayon de la grande poulie
r : rayon de la petite poulie
d : entraxe
> Longueur d'une partie tendue rectiligne = racine [d² - (R-r)²]
(à multiplier par deux, donc ...)
> alpha = arctg [(R-r)/d]
Longueur de la courroie =
(pi + 2 *alpha)*R + racine [d² - (R-r)²] * 2 + (pi - 2 *alpha)*r
Merci, à bientôt,
Il aurait pu pleuvoir, con comme il est ! (Coluche)
#24 - 13-03-2011 14:35:25
- dhrm77
- L'exilé
- Enigmes résolues : 49
- Messages : 3004
- Lieu: Fanning Island-?-Lac Tele,Mali
22, v'la less poulies !
Avec un peu de retard, je trouve:
2×(√35+5×3.1415926535÷2+cos⁻¹ (√35÷6)) = 27.875018992
Mais je voulais rajouter que dans la pratique, par exemple quand on attache le moteur du tracteur a la moissoneuse-batteuse, la courroie est en fait plus longue que mathematiquement necessaire et le poids meme de la courroie realise la tension necessaire au transfer du mouvement.
Si la courroie etait de longueur exacte, quand le raccord (et il y a toujours un raccord quelque part) passe par une extremité, la tension augmente et pourrait la faire rompre.
Dans la pratique le mou sert aussi a absorber les accelerations et decellerations rapides.
Dans une perceuse a colonne (ou la courroie peut etre placée a plusieurs niveaux differents), le moteur se deplace pour ajuster la tension.
Great minds discuss ideas; Average minds discuss events; Small minds discuss people. -Eleanor Roosevelt
#25 - 13-03-2011 14:48:12
- L00ping007
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 2010
- Lieu: Paris
22, v'la le poulies !
J'ai une question : le calcul que j'ai fait, comme d'autre avec moi, est-il correct ?
Car on a considéré que le câble était tangent aux sommets des cercles, ce qui n'est manifestement pas le cas !
Mais on trouve tout de même un résultat identique ?!?
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum









