 |
#1 - 24-03-2011 20:00:39
- looozer
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 697
- Lieu: Belgique
enigme 10-girale
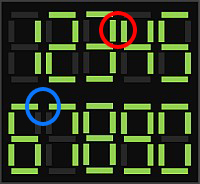
Deux digits sont dits "aboutables" si l'on peut les joindre par l'extrémité libre d'un de leurs segments horizontaux (exemple 6 et 7 sont "aboutables").
Deux digits sont dits "accolables" si l'on peut les accoler par au moins un segment vertical (exemple : 3 et 4 sont "accolables"). Attention, 1 n'est "accolable" qu'à droite!
1. Quel est le plus grand nombre que l'on peut construire en aboutant des digits, chacun étant utilisé au maximum une fois?
2. Quel est le plus grand nombre que l'on peut construire en accolant des digits, chacun étant utilisé au maximum une fois?
Remarques :
- Une extrémité est libre quand elle n'appartient qu'à un seul segment du digit.
- Accoler deux segments verticaux consiste à les coller sur toute leur longueur.
#2 - 24-03-2011 20:49:23
- medihv
- Professionnel de Prise2Tete
- Enigmes résolues : 47
- Messages : 123
enigme 10-fitale
1. Je dirai donc que le plus grand est 98765320.
Pour la 2, la je cherche encore, ça va commencer par 9 mais il faut faire attention avec le reste pour placer un max de digits 
#3 - 24-03-2011 20:53:36
- FRiZMOUT
- Verbicruciste binairien
- Enigmes résolues : 49
- Messages : 2218
#4 - 24-03-2011 21:02:46
- looozer
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 697
- Lieu: Belgique
enigme 10-gitalr
medihv et Frizmout : si on considère qu'un digit est formé dans une matrice de 6 points et 7 segments, une extrémité est libre quand elle n'appartient qu'à un seul segment du digit. Le segment horizontal du 4 n'a donc aucune extrémité libre. Désolé si mon énoncé n'était pas assez clair. Je ne peux donc pas accepter votre première réponse.
#5 - 24-03-2011 21:05:49
- gasole
- Elite de Prise2Tete
- Enigmes résolues : 40
- Messages : 1117
- Lieu: Toulouse
Enigm e10-gitale
Une question : "1 n'est accolable qu'à droite" : c'est 15 qui est bon ou 51 ?
#6 - 24-03-2011 21:17:52
- looozer
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 697
- Lieu: Belgique
Enimge 10-gitale
FRiZMOUT: 6 et 4 ne sont pas "accolables" dans cet ordre
gasole : 15 est un bon collage, pas 51
#7 - 24-03-2011 21:18:29
- FRiZMOUT
- Verbicruciste binairien
- Enigmes résolues : 49
- Messages : 2218
Enigme 10-gital
Oh OK. 6257 et 79862504 conviendraient mieux, alors ?
#8 - 24-03-2011 21:31:44
- gasole
- Elite de Prise2Tete
- Enigmes résolues : 40
- Messages : 1117
- Lieu: Toulouse
Enigme 10-gitlae
Ok mais ça change rien en fait, 3 et 7 aussi ne sont accolables qu'à droite, et autant utiliser le plus grand, 7, on n'utilisera donc pas le 1 ni le 3. Il faudra donc essayer de placer 02456789, 7 en tête car accolable à droite seulement, et ensuite on retient le plus grand possible.
Pour la question 1 : 6257
Pour la question 2 : 79862504
#9 - 24-03-2011 21:53:33
- looozer
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 697
- Lieu: Belgique
Enigme 10-giitale
Bonnes réponses de FRiZMOUT et gasole 
#10 - 24-03-2011 22:13:44
- L00ping007
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 2010
- Lieu: Paris
Enigme 10-gtiale
Les seuls digits aboutables sont : 2,3,5,6,7,9.
- 3,7,9 sont aboutables à gauche, donc ils doivent terminer le nombre cherché.
- 2 peut être suivi d'un 3, d'un 5, ou d'un 9.
- 5 peut être suivi d'un 2, d'un 3, ou d'un 7.
- 6 peut être suivi d'un 2, d'un 3, ou d'un 7.
Si on essaie de prendre 6 comme premier chiffre (le plus à gauche dans l'écriture en base 10), on a intérêt à prendre 2 comme chiffre suivant (sinon on termine le nombre avec 3,7, ou 9).
Ensuite, on a le choix entre 3,5, et 9, donc autant prendre un 5.
Puis on a le choix entre 3 et 7 (2 est déjà pris), donc autant prendre 7.
On arrive au nombre 6257
Peut-on faire mieux ?
En commençant par 5, on fait suivre par un 2, et on doit terminer avec 3 ou 9. On plafonne à 529.
En commençant par 2, on fait suivre par un 5, puis on termine avec 3 ou 7. On plafonne à 257.
Le plus grand nombre aboutable est donc 6257
Pour les nombres accollables, 1,3,7 ne le sont qu'à droite. Ils doivent donc être placés le plus à gauche possible du nombre, et seul un des 3 peut être utilisé. Autant prendre le 7. Du coup 1 et 3 ne seront pas utilisés.
Ensuite, on prend les plus grands : 9, puis 8, puis 6.
Là il nous reste 0,2,4,5. Seul 2 est accollable après le 6, donc on poursuit avec 2.
On continue avec 5 (plutôt que 4 ou 0), puis 0 (forcé), et enfin le dernier 4.
Le plus grand nombre accollable est donc 79862504
#11 - 24-03-2011 22:32:05
- langelotdulac
- Ange de Prise2Tete
- Enigmes résolues : 49
- Messages : 2963
- Lieu: Paradis
Engme 10-gitale
Tu es largement assez dingo pour qu'un Minito te semble cohérent \o/ !
#12 - 24-03-2011 22:47:12
- mitsuidewi
- Professionnel de Prise2Tete
- Enigmes résolues : 49
- Messages : 250
- Lieu: dans une chambre universitaire
#13 - 24-03-2011 23:02:59
- looozer
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 697
- Lieu: Belgique
Enigme 10-gitalle
L00ping700 et mitsuidewi : bonnes réponses
langelotdulac : une sur deux
#14 - 24-03-2011 23:09:00
- langelotdulac
- Ange de Prise2Tete
- Enigmes résolues : 49
- Messages : 2963
- Lieu: Paradis
Engime 10-gitale
Euh ... Laquelle ? 
Tu es largement assez dingo pour qu'un Minito te semble cohérent \o/ !
#15 - 24-03-2011 23:26:19
- looozer
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 697
- Lieu: Belgique
Enigme 10-gitlae
langelotdulac : tu as bien abouté 
#16 - 24-03-2011 23:59:25
- franck9525
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1935
- Lieu: 86310
enigme 10-gitzle
1. 4 digits max, 6257
1, 4, 8 et 0 ne sont pas aboutables
3, 7 et 9 ne sont aboutables que par la gauche, donc termine le nombre.
2. 8 digits max, 12456890
1, 3 et 7 ne sont accolables que par la droite donc commence le nombre.
EDIT:
je n'avais pas noté qu'il fallait proposer le plus grand possible et
non juste le plus long : 79 862 504

The proof of the pudding is in the eating.
#17 - 25-03-2011 00:59:17
- dhrm77
- L'exilé
- Enigmes résolues : 49
- Messages : 3004
- Lieu: Fanning Island-?-Lac Tele,Mali
Enigme 10-gital
1. 6257
2.79862450
2.79862504
Great minds discuss ideas; Average minds discuss events; Small minds discuss people. -Eleanor Roosevelt
#18 - 25-03-2011 06:49:39
- halloduda
- Professionnel de Prise2Tete
- Enigmes résolues : 24
- Messages : 495
- Lieu: Ardèche
Enigem 10-gitale
1. aboutable 6257
2. accolable 79862450
#19 - 25-03-2011 07:10:31
- medihv
- Professionnel de Prise2Tete
- Enigmes résolues : 47
- Messages : 123
Eigme 10-gitale
Pour la 2 je dirai 79860452 mais avec la certitude qu'il y a mieux, je pense 
#20 - 25-03-2011 09:51:44
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3501
- Lieu: 94110
Enigme 10-ggitale
2 et 5 sont les seuls chiffres aboutables de chaque coté.
6 est seulement aboutable à droite, 3, 7 et 9 aboutables à gauche.
Je commence par le 6, j'enchaîne avec 2 et 5, et je termine avec le chiffre aboutables à gauche par le haut le plus grand, soit 7.
Ce qui donne 6257.
1 3 et 7 ne sont accolables qu'à droite, je commence donc par 7.
Je complète avec les autres en commençant par les plus grands.
Et j'obtient : 79856240.
#21 - 25-03-2011 10:14:19
- Nicouj
- Professionnel de Prise2Tete
- Enigmes résolues : 27
- Messages : 330
EEnigme 10-gitale
6257
edit: 7986245
79862450
#22 - 25-03-2011 10:41:07
- LeSingeMalicieux
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1298
- Lieu: Haute-Marne
Enigm 10-gitale
J'aboute 6257, et j'accole 79862504 
Avoir quatre mains, c'est plus pratique pour taper sur un clavier.
#23 - 25-03-2011 14:49:05
- Oups!
- Passionné de Prise2Tete
- Enigmes résolues : 42
- Messages : 58
- Lieu: entre Roazhon et Naoned
nigme 10-gitale
accolé : 79862450
abouté : 6257
#24 - 25-03-2011 16:18:27
- looozer
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 697
- Lieu: Belgique
enigme 10-gitzle
Bonnes réponses de LeSingeMalicieux!
franck9525, dhrm77, halloduda, medihv, Oups! : votre accolage est améliorable
Jackv : 6 et 5 ne sont pas accolables dans cet ordre
Nicouj : pourquoi as-tu gardé le 0 dans ta poche?
#25 - 25-03-2011 16:33:00
- Klimrod
- Elite de Prise2Tete
- Enigmes résolues : 40
- Messages : 4050
- Lieu: hébesphénorotonde triangulaire
nEigme 10-gitale
Ton exercice n'est pas aussi trivial qu'il n'en parait...
1. le plus grand nombre que l'on peut construire en aboutant des digits, chacun étant utilisé au maximum une fois : 6257
2. le plus grand nombre que l'on peut construire en accolant des digits, chacun étant utilisé au maximum une fois : 79862504
Hum... pas sûr de mon résultat...
Klim.
J'ai tant besoin de temps pour buller qu'il n'en reste plus assez pour bosser. Qui vit sans folie n'est pas si sage qu'il croit.
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum









