L9=5+-1cm.
Propriété des cotés voisins: un sommet est à égale distance des 2 points tangents au cercle....

Quand tu dis tangents extérieurement à un cercle. Tu veux dire qu'il s'agit d'un seul cercle à l'intérieur du polygone, donc chaque côté est tangent à ce cercle? ou bien que les 9 côtés sont tangents à 9 cercles différents se trouvant à l'extérieur du polygone ? La 1ere proposition me parait plus censée.

Appelons r le rayon du cercle et L la longueur du 9ème segment.

Alors :
[TeX]2 \pi = Arctg(\frac{1/2}{r}) + Arctg(\frac{2/2}{r}) + Arctg(\frac{3/2}{r}) + Arctg(\frac{4/2}{r}) + Arctg(\frac{5/2}{r}) + Arctg(\frac{6/2}{r}) + Arctg(\frac{7/2}{r}) + Arctg(\frac{8/2}{r}) + Arctg(\frac{L/2}{r})[/TeX]
[TeX]2 \pi = Arctg(\frac{1}{2r}) + Arctg(\frac{2}{2r}) + Arctg(\frac{3}{2r}) + Arctg(\frac{4}{2r}) + Arctg(\frac{5}{2r}) + Arctg(\frac{6}{2r}) + Arctg(\frac{7}{2r}) + Arctg(\frac{8}{2r}) + Arctg(\frac{L}{2r})[/TeX]
On peut utiliser la formule [latex]Arctg(1/x) = \pi /2 - Arctg(x)[/latex]
Ce qui nous amène à :
[TeX]2 \pi = Arctg(2r) + Arctg(\frac{2r}{2}) + Arctg (\frac{2r}{3})+ Arctg (\frac{2r}{4}) + Arctg(\frac{2r}{5}) + Arctg(\frac{2r}{6}) + Arctg(\frac{2r}{7}) + Arctg(\frac{2r}{8}) + Arctg(\frac{2r}{L})[/TeX]
Reste à résoudre cette équation en se débarrassant du rayon r. Et c'est trop compliqué pour moi...
Klim.

Bon j'ai fais le calcul grâce à un dessin approximatif, et j'ai simplement compté en partant d'une propriété "Les longueurs des segments tangents"

Et je trouve que le 9eme côté a pour longueur : 5cm.

Le problème ne me paraît pas complètement contraint, et on peut obtenir à peu près ce que l'on veut.

Par exemple sur l'exemple suivant, où les 7 premiers segments dont la somme des longueurs est 28 sont tous tangents au cercle en un même point et où le neuvième peut faire par exemple 28 cm.
                     
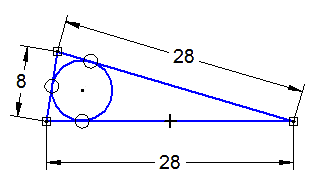
Tu voulais peut-être dire que les points de tangence doivent appartenir à chacun des segments ?

Alors, je pense que le neuvième pourrait faire à peu près 5 cm ...

J'avais bien l'encadrement 4<x<6  mais j'avais essayé de trouver la valeur exacte de x alors que ça n'était pas demandé

Y'a-t-il un moyen simple de l'obtenir ???

Vasimolo

En fait la question ne demande qu'une valeur approchée à 1 près donc 5 convient parfaitement ( c'est même la seule valeur que l'on peut donner avec certitude sans autre calcul ) . Mais bon la bonne réponse est peut-être 4,1 et alors la réponse 5 est un peu décevante

Vasimolo