Forum dédié aux énigmes et à toutes formes de jeux de logique. | Déconnexion |
|
Tu n'es pas identifié sur Prise2tete : s'identifier.  Accueil Accueil
 Forum Forum
|
 |
#1 - 22-06-2011 00:07:19
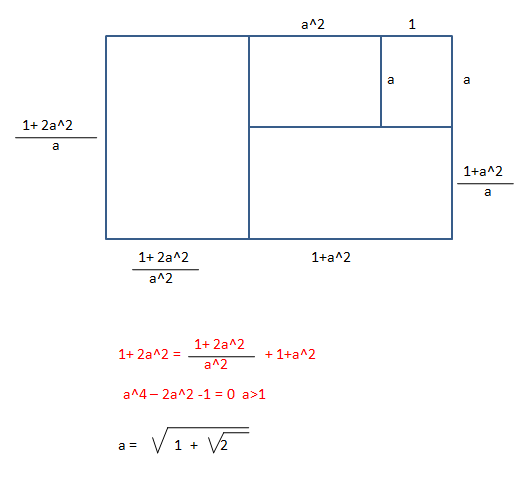
Glacèrent le sel..Dans la figure ci-dessous, les rectangles ABCD, AEFD, CFGH, EIJG, et BIJH sont tous semblables. Trouver AB/BC. C'est à l'intelligence d'achever l'oeuvre de l'intuition.
#0 Pub#2 - 22-06-2011 00:40:50
Glaèrent le sel...Bonjour, #3 - 22-06-2011 10:54:27
glacèrent le del...BJ/BH=IJ/EJ=CH/CF=AE/AD=AB/BC Podcasts Modern Zeuhl : http://radio-r2r.fr/?p=298 #4 - 22-06-2011 12:23:30
glacèrent le qel...Posons JB=1etJI=x. Alors : #5 - 22-06-2011 16:27:28
Glacèrent lee sel...Salut, #6 - 22-06-2011 16:28:45
glacèrent le sek...Excellent, Clydevil. C'est à l'intelligence d'achever l'oeuvre de l'intuition. #7 - 22-06-2011 17:10:00#8 - 22-06-2011 18:34:47#9 - 22-06-2011 21:03:03#10 - 22-06-2011 22:02:26
glacèrznt le sel...Je pose BJ=1 et BH=k The proof of the pudding is in the eating. #11 - 22-06-2011 22:16:36
glacèrrnt le sel...Pour looozer, "glacèrent les" = anagramme de "les rectangles", puis petit effet palindromique sur "les" pour former "le sel", juste pour la forme ! C'est à l'intelligence d'achever l'oeuvre de l'intuition. #12 - 22-06-2011 23:58:39
Glacèrent le sel..Salut ! #13 - 23-06-2011 00:06:02
flacèrent le sel...Bravo Golgot ! C'est ma solution à 2 ou 3 mots près ! C'est à l'intelligence d'achever l'oeuvre de l'intuition. #14 - 23-06-2011 04:58:30#15 - 23-06-2011 07:08:19
Glacèrent le sl...dhrm, il te manque un petit quelque chose... C'est à l'intelligence d'achever l'oeuvre de l'intuition. #16 - 23-06-2011 08:48:52
glacèrent le qel...Bonjour, J'ai tant besoin de temps pour buller qu'il n'en reste plus assez pour bosser. Qui vit sans folie n'est pas si sage qu'il croit. #17 - 23-06-2011 11:08:18
glacèrenr le sel...Je pose k=ABBC. #18 - 23-06-2011 11:17:46#19 - 23-06-2011 17:59:13#20 - 24-06-2011 08:45:18
glacèrent ke sel...Oui aux trois dernières réponses ! C'est à l'intelligence d'achever l'oeuvre de l'intuition. Réponse rapideSujets similaires
Mots clés des moteurs de recherche
|
 | ||||||||||||||||||||||||||||||||
| Prise2Tete Forum Statistiques Liste des membres Hall of Fame Contact | ||||||||||||||||||||||||||||||||||
Un jeu où seules la réflexion, la logique et la déduction permettent de trouver la solution.