 |
#1 - 02-09-2011 23:36:58
- w9Lyl6n
- Professionnel de Prise2Tete
- Enigmes résolues : 26
- Messages : 220
le jeu de fjali
Djali est une chèvre particulière : Quand on lui présente un nombre écrit avec des cartes présentant les chiffres de 0 à 9, elle échange avec sa petite patte les chiffres voisins comme sur le dessin:
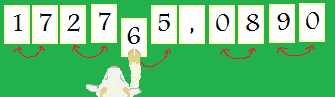
(ne vous moquez pas de ma chèvre elle est très susceptible  ) )
f(12) = 21
f(65,9) = 56,09
f(3,141592) = 30,415129
f(142,347) = 1024,4307
...
Avec sont air innocent, Djali à mit au jour une fonction déroutante, et elle vous met au défit d'y comprendre quelque chose. Elle, évidemment, elle a déjà tout compris...
Serez vous aussi fort que Djali ?
(Les réponses sont a justifier  ) )
(1) La fonction est elle bijective?
(2) Où est elle continue, discontinue, et pourquoi?
(3) Serez vous capable de donner un graphe de la fonction et d'expliquer ce qu'on voit?
(4) Quelles sont les symétries de ce graphe :
a) axiale?
b) centrale?
c) invariant par translation?
d) invariant par certaines homothétie?
e) des motifs se répètent?
(5) Est elle intégrable? dérivable en certains points?
(6) Si vous trouvez d'autre choses intéressantes... 
Mais non c'est pas dur, puisque Djali y est arrivée...
Amusez vous bien 
#2 - 03-09-2011 12:46:07
- w9Lyl6n
- Professionnel de Prise2Tete
- Enigmes résolues : 26
- Messages : 220
le jeu de djami
Suite à un message privé de Clydevil je précise que c'est l'écriture propre des nombres décimaux qu'il faut utiliser dans la fonction (celle qui se termine par une infinité de 0, et pas une infinité de 9). En générale c'est toujours la norme, je ne voulais pas vous embêter avec ça, mais c'est pas moi qui ai commencé 
#3 - 03-09-2011 19:20:47
- L00ping007
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 2010
- Lieu: Paris
Le jeu dee Djali
Si j'ai bien compris, on part de la virgule, dans un sens ou dans l'autre, en prenant les chiffres 2 par 2.
Du coup, la fonction f vérifie fof=Id, et du coup elle es bijective (injective et surjective se déduisent de cette relation)
Pour la continuité, j'aurais tendance à dire qu'elle l'est partout à droite, mais pas à gauche sur les décimaux. En revanche, peut être sur les nombres à écriture décimale infinie, c'est a dire non décimaux, il y a sans doute continuité a gauche. Pour une preuve, on utilise le fait que le dernier chiffre change quand on s'approche par la gauche (inférieur d'une unité) donc ça change la valeur. Mais pour les autres, il n'y a pas de dernier chiffre...
Pour le reste, c'est à suivre 
Mais j'aimerais tout de même avoir un retour sur mes premières affirmations 
#4 - 03-09-2011 20:07:57
- w9Lyl6n
- Professionnel de Prise2Tete
- Enigmes résolues : 26
- Messages : 220
Le jue de Djali
L00ping007 : Spoiler : [Afficher le message] Oui, c'est juste. C'est cette fonction qui a motivé ma précédente énigme http://www.prise2tete.fr/forum/viewtopic.php?id=9572. Je suis contant que tu ais retrouvé ces résultats sans faire le lien avec
#5 - 03-09-2011 20:51:06
- L00ping007
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 2010
- Lieu: Paris
eL jeu de Djali
Effectivement je n'avais pas lu ton précédent topic, il me paraissait trop compliqué, mais dans ce sens-là, montrer des propriétés, c'est plus mon truc 
Je vais réfléchir à la suite sans me faire spoiler par l'autre topic ;-)
#6 - 04-09-2011 12:39:12
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
lr jeu de djali
Ce que je vois dans cette fonction:
Bien sûr bijective et aussi f(f(x))=x donc symétrie par l'axe y=x.
Si on trace le graphe des entiers de 00 à 99, on définit une trame qui est le modèle de bas d'une fractale: si on zoome sur un point particulier, entre ce point et le point immédiatement supérieur, on va retrouver un ensemble de 100 oints qui auront la même forme que la trame de base, et ainsi de suite.
Evidemment cette fonction n'est donc pas continue.
#7 - 04-09-2011 16:23:21
- w9Lyl6n
- Professionnel de Prise2Tete
- Enigmes résolues : 26
- Messages : 220
Le ju de Djali
nodgim : Un très bon résumé des propriétés géométriques, mais il reste à en prouver plusieurs. Attention il n'y a rien d'évident sur la continuité, le graphe est trompeur!
Indice pour prouver les propriétés géométriques:
Spoiler : [Afficher le message] Dans l'expression de la fonction, il y a un genre de linéarité pour les puissances de 100 distinctes.
#8 - 04-09-2011 20:17:44
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3230
- Lieu: Luxembourg
LLe jeu de Djali
Bonjour,
Cette fonction est vraiment très intéressante.
(1) Elle est bijective: on a même pour tout x du Df: f[f(x)]=x
(2) Elle est discontinue car dans [f(x);f(x+e)], il y a plein de points qui ont leurs antécédents hors de [x;x+e]
(3) Son graphe devrait être un nuage de points (une nébuleuse ?)
(4) Son graphe est symétrique par rapport à la diagonale (d'équation y=x)
(5) Je ne pense pas qu'elle soit ni intégrable ni dérivable du fait de sa "forte" discontinuité
Bonne soirée.
Frank
#9 - 05-09-2011 18:11:56
- w9Lyl6n
- Professionnel de Prise2Tete
- Enigmes résolues : 26
- Messages : 220
le jei de djali
Franky1103 : oui pour (1), non pour (2) -> ce n'est pas la définition de la continuité, la fonction n'est pas discontinue partout.
(3) : mais encore 
oui pour (4) non et oui pour (5)
Comme je l'ai dit c'est une fonction déroutante 
#10 - 08-09-2011 23:47:38
- w9Lyl6n
- Professionnel de Prise2Tete
- Enigmes résolues : 26
- Messages : 220
le jeu de djalo
Encore une solution à rallonge que 3 personnes seulement vont lire en entier  

(1) La fonction est bijective car f(f(x))=x
(2) La fonction est discontinu en tout nombre décimal à gauche et continue ailleurs (à droite pour les décimaux, à gauche et à droite pour les non décimaux)
(3) 
La courbe est une fractale : le motif comprit dans [0,1]x[0,1] se répète à différentes échelles.
(4a) le graphe est symétrique par rapport à la droite x=y toujours parce que f(f(x))=x
(4b) le graphe est symétrique par rapport à l'origine car f(-x)=-x
(4c) le graphe n'est pas invariant par translation mais tout sous partie du graphe du coté des abscisses positives (respectivement négatives) se répète une infinité de fois de manière translaté
(4d) Toute homothétie de centre l'origine et de rapport 100n où n est un entier relatif laisse invariant le graphe.
(4e) Comme on l'a dit le graphe est totalement fractal
(5) la fonction est intégrable mais dérivable nulle part.
Un petit résultat qui sera utile partout pour les preuves:
lemme :Si n est un entier positif, m un entier relatif et x∈[0,1[ alors :
f((n+x)100m) = f(n)100m + f(x)100m
Exemple : f(1234,56) = f(12)x100 + f(0,3456)x100, ce résultat se justifie visuellement.
preuve (2):
je vais la simplifier au maximum :
Pour les décimaux :
Ce sont les nombres où on passe d'une écriture qui se termine par une infinité de 9 à gauche, à une infinité de 0 à droite.
On passe de ...a(b-1)999999... à ...ab0000000... (a et b ainsi que b-1 sont des chiffres, b n'est pas nul)
1er cas :
f échange a et b alors f(...a(b-1)999999...) = ...(b-1)a9999999
f(...ab0000000...) = ...ba0000000... à cause de la retenu amené par les 9999...
le chiffre "a" n'est pas le même, les nombres sont différents
2eme cas :
f échange b et 0 alors f(...xa(b-1)999999...) = ...ax9(b-1)9999999... = ...ax9b0000000...
f(...xab0000000...) = ...ax0b0000000... la différence est encore plus évidente : un 9 devient 0
Pour la continuité à droite on se réfère à ce qui suit, le principe est exactement le même :
Pour les NON décimaux :
Soit x un nombre non décimal de [0,1[, n un entier, on va montrer que si x et y ont leurs 2n premières décimales en commun alors |f(x)−f(y)|<100−n
décomposons x et y : x=(a+b)100−n,y=(a+c)100−n
alors (lemme) :
|f(x)−f(y)| = | (f(a)−f(a))100−n+(f(b)−f(c))100−n|= |f(b)−f(c)|100−n<100−n
En effet pour tout k dans [0,1[ , f(k) est lui aussi dans [0,1[
Donc f est bien continue en x
Pour étendre le résultat au reste des non décimaux on utilise la "pseudo linéarité" avec les puissance de 100 (lemme) pour se ramener à [0,1[.
preuve (3):
on calcul f(00),f(01) jusqu'à f(99) :
00,10,20...,90, 01,11,21..,91 02,12,..92 ... 08,18,28...,98 09,19,29,39...89,99 cela donne des séries de 10 points aligné suivant une pente de 10x verticalement (ou x/10 horizontalement)
Ensuite tout découle encore une fois du lemme, exemple : f(56+x)=65+f(x)
Quand x parcourt [0,1[ on retrouve le graphe de f sur [0,1[ translaté du vecteur (56,65)
preuve (4d):
Tout découle directement du lemme :
f(100nx)=100nf(x)
preuve (5):
Montrer que f est intégrable se fait avec des sommes de Riemann en minorant est en majorant f sur chaque intervalle. Montrer que les sommes inférieur et supérieur de rectangles sont adjacentes est difficile car il faut prendre en considération la fréquence et l'amplitude des discontinuités.
Pour se persuader du résultat, on peut observer l'aire sous la courbe avec la fonction analogue pour l'écriture binaire (par soucis de visibilité):
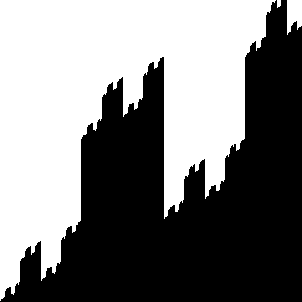
Enfin la fonction n'est dérivable nulle part, mais là j'en ai vraiment assez d'écrire 
A plus tard pour de nouvelles énigmes moins ch***** à rédiger 
#11 - 09-09-2011 12:48:04
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
le jei de djali
Je parle pour moi mais il me semble que poser une dizaine de questions très ouvertes pour un seul problème n'est pas très motivant . Trouver la bonne question qui va motiver les troupes et prolonger le sujet au cas où ...
Ceci dit j'ai vraiment bien aimé la bijection continue uniquement sur R\D 
Vasimolo
#12 - 09-09-2011 14:22:19
- w9Lyl6n
- Professionnel de Prise2Tete
- Enigmes résolues : 26
- Messages : 220
le jeu dz djali
Oui je m'en suis rendu compte, notamment en rédigeant ma solution 
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum










