Enigme Hum, suite hum... @ Prise2Tete

nodgim · #1

Bonjour à tous

Cette suite est définie de la manière suivante:
On passe d'un nombre au suivant en ajoutant ou ôtant 1 ou 10. Toutes les valeurs de cette suite sont des entiers compris entre 0 et 99 inclus.

Soit A un nombre compris entre 0 et 9 et qu'on veut déplacer à une valeur comprise entre 90 et 99 en se servant de la suite.
Soit B un nombre du groupe (0;10;20;..90) et qu'on veut déplacer dans le groupe (9;19...99) en se servant de la suite.

Contrainte: Pour les nombres du groupe (0;10..90) on ne peut retrancher -1.

Trouver une suite pour un nombre A et une suite pour un nombre B tel qu'aucun nombre de la suite A ne se trouve dans la suite de B et vice versa.

Bon courage.

golgot59 · #2

Salut !

Bon, je ne suis pas sûr d'avoir bien compris l'énoncé. Pour expliquer mon problème, autant proposer une réponse que je suppose erronée :
S={1,2,3,4,5,6,7,8,9,8,18,28,38,48,58,68,78,88,98,88,78,68,58,48,38,28,18,8,7,6,5,4,3,2,1,0,10,20,30,40,50,60,70,80,90,89}

Tous les nombres de la suite A mènent bien à 98 sans passer par B, et tous ceux de la suite B mènent à 89 sans passer par A !

(J'ai supposé que le 0 n'était pas dans les deux suites... ? Je l'ai donc enlevé de la suite A, mais ça reviendrait au même pour la suite B)

nodgim · #3

Pour te dire si c'est vrai ou faux, donne moi d'abord les 2 suites, celle de A et celle de B. Ce sont 2 suites distinctes puisqu'aucun des nombres n'est commun, donc y compris le 0.

golgot59 · #4

Ah, il y a 2 suites distinctes !!!

Bon, alors il suffit de scinder la mienne en 2 (et du coup je peux ajouter le 0).

S.A={0,1,2,3,4,5,6,7,8,9,8,18,28,38,48,58,68,78,88,98}

Tous les nombres de A mènent à 98.

et

S.B={0,10,20,30,40,50,60,70,80,90,89}

Tous les nombres de B mènent à 89.

FRiZMOUT · #5

Je ne comprends pas bien ton histoire de groupe.
En prenant la suite B, B+10, (B+10)-1 pour B et A, A+10, A+2*10, ... , A*9*10 pour 0<A<9, ça marche, non ?
Après il suffit d'ajouter 1 (respectivement ôter 1) pour A=0 (resp pour A=9) en début de suite pour avoir quasiment tous les cas possibles.
Bon, en fait, c'est quoi la question ?

nodgim · #6

Une précision: la question est de trouver (au moins) une suite pour un nb A donné et une suite pour un nombre B donné, il n'est pas demandé de trouver ttes les possibiltés (sauf si vous êtes très très courageux!)

Klimrod · #7

Si j'ai bien compris, tu veux qu'on te donne une suite qui permet de passer d'un nombre A choisi dans la colonne bleue à gauche à un nombre A' qui est son alter ego dans la colonne bleue à droite et une suite qui permet de passer d'un nombre B dans la ligne rouge en haut à un nombre B' qui est son alter ego dans la ligne rouge en bas.
Les suites se construisent en avançant d'une case adjaçante, mais jamais en diagonale. Et il ne faut pas que les suites se croisent sur une même case.

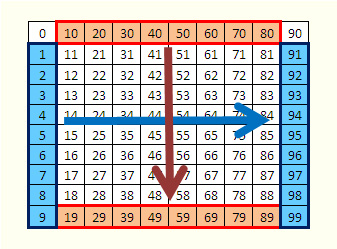
Eh bien, si c'est ça, j'ai l'impression que ce n'est pas possible...
Klim.

golgot59 · #8

D'autant, Klim, que le 0 doit être rouge et bleu, puisqu'il est dans les deux groupes A et B, et qu'il ne doit pas se trouver dans "l'autre groupe", c'est à dire ni dans B ni dans A...

nodgim · #9

Un grand bravo à Klimrod qui a bien compris l'astuce en positionnant les 100 nombres dans un carré! C'est exactement la preuve attendue.
Etonnant, non ?

nodgim · #10

golgot59 a écrit:
D'autant, Klim, que le 0 doit être rouge et bleu, puisqu'il est dans les deux groupes A et B, et qu'il ne doit pas se trouver dans "l'autre groupe", c'est à dire ni dans B ni dans A...

Pour le zéro, c'est soit A soit B qui peut prendre la case, mais pas les deux. Ce n'est pas en contradiction avec l'énoncé du problème.

golgot59 · #11

Bon, j'ai pas dû bien comprendre ta réponse :

Ce sont 2 suites distinctes puisqu'aucun des nombres n'est commun, donc y compris le 0.

J'avais compris que ça signifiait que le 0 devait être dans les deux suites.

Enfin, pas grave

nodgim · #12

Si le zéro était commun, il y aurait des solutions!

Klimrod · #13

Bah non ! Je ne crois pas...

nodgim · #14

Ben si par exemple:
A (0,10,20,..90) et B(0,1,2,3,...9).
Il n'y a qu'à regarder le tableau pour s'en persuader.

Klimrod · #15

Dans ce cas, les deux suites se croisent en 0 !

nodgim · #16

Ben oui, enfin ne se croisent pas mais démarrent du même endroit.

Bamby2 · #17

quelqu'un aurait un exemple de solution ? car la j'avoue ne pas comprendre comment c'est possible

nodgim · #18

Bamby, observe le tableau de Klimrod, tu comprendras.

Bamby2 · #19

j'ai beau regarder,

si je prends A= 7 et B=10,
je ne peux trouver de suite tel que
7 deviennent un nombre entre 90 et 99 et
10 devienne un nombre x9 ....

Quelqu'un pour me donner la solution s'il vous plait,
J'arriverai surement a comprendre sur a l'aide d'un exemple.

j'avoue que je sèche complètement, j'ai du mal comprendre un truc.

merci d'avance.

nodgim · #20

Bamby, colorie un parcours de A et colorie un parcours de B, tu te rendras compte que les chemins de chacun d'eux sont continus et que le croisement est obligatoire, et donc qu'il existe forcément une case commune.

Bamby2 · #21

han, fallait "montrer" que c’était pas possible ?

a ben la d'un coup je comprends

merci.

Forum dédié aux énigmes et à toutes formes de jeux de logique.	Déconnexion
Tu n'es pas identifié sur Prise2tete : s'identifier. Accueil Forum	[+]

#1 - 24-09-2011 08:36:41

Hum, sute hum...

#0 Pub

#2 - 24-09-2011 17:02:46

hul, suite hum...

#3 - 24-09-2011 17:26:30

Hum, suite hum..

#4 - 24-09-2011 18:51:59

Hum, suiite hum...

#5 - 24-09-2011 18:59:43

Hum, site hum...

#6 - 25-09-2011 09:06:07

hum, suire hum...

#7 - 27-09-2011 10:18:21

Hum, suite humm...

#8 - 27-09-2011 14:19:30

uHm, suite hum...

#9 - 27-09-2011 17:36:14

Hum, siute hum...

#10 - 28-09-2011 20:01:05

hum, duite hum...

golgot59 a écrit:

#11 - 29-09-2011 15:14:25

Hum, suie hum...

#12 - 29-09-2011 17:27:01

Hum, suite hm...

#13 - 29-09-2011 17:31:11

Hum, suit hum...

#14 - 29-09-2011 17:55:05

Hu, suite hum...

#15 - 29-09-2011 17:56:17

Hum suite hum...

#16 - 29-09-2011 18:50:00

um, suite hum...

#17 - 29-09-2011 18:53:42

Hu, suite hum...

#18 - 29-09-2011 18:59:24

hum, suiye hum...

#19 - 01-10-2011 00:54:18

Humm, suite hum...

#20 - 01-10-2011 12:01:11

Hum, ssuite hum...

#21 - 01-10-2011 12:40:08

hul, suite hum...

Réponse rapide

Sujets similaires

Mots clés des moteurs de recherche

Pied de page des forums