Pour des raisons pratiques, ramenons-nous, sans perte de généralité dans la démonstration, à un cas théorique où hommes et femmes sont vraiment collés les uns aux autres, autrement dit à une droite sur laquelle les points a, b, c, d, e, f, g sont confondus avec les points équidistants A, B, C, D, E, F, G mais pas nécessairement dans cet ordre, et où la distance entre deux points voisins vaut 1.

Toute permutation de a, b, c, d, e, f, g peut être obtenue à partir d'une configuration où ces points sont confondus respectivement avec A, B, C, D, E, F, G par une suite de permutations "élémentaires" de type "j'inverse les places de deux de ces points" (je demande à deux des femmes d'échanger leur place). L'échange des points x et y ajoutera un nombre pair (positif ou négatif) à la valeur |xX|+|yY|, car :

- si |xy| est paire, on ajoutera ou enlèvera un nombre pair à |xX| et à |yY| ;
- si |xy| est impaire, on ajoutera ou enlèvera un nombre impair à |xX| et à |yY|.

Finalement, quelle que soit la permutation des points a, b, c, d, e, f et g, la somme des distances parcourues par les cavaliers pour aller rejoindre leurs cavalières, c'est-à-dire |aA|+|bB|+|cC|+|dD|+|eE|+|fF|+|gG|, est paire.

Or, comme la distance maximale entre deux points vaut 6, il aurait fallu que les sept distances prennent toutes les valeurs entre 0 et 6 pour qu'il n'existe pas deux cavaliers parcourant la même distance, ce qui aurait donné le nombre impair 21 comme somme des distances. Ce cas est impossible, donc il y aura toujours au moins deux hommes qui parcourront la même distance pour rejoindre leurs promises respectives.

J'espère avoir été à peu près clair... Vu l'heure qu'il est, je ne promets rien

On va faire la version un peu plus flemmard.

Disons qu'au lieu de traverser la salle en direction de leur cavalière, les hommes échangent de place entre eux jusqu'à se retrouver en face d'elles.

Fondamentalement ça change strictement rien au problème.

Bien maintenant il suffit de s'apercevoir qu'il n'y a que 7 distances possibles.

La distance 0 : Rester sur place
La distance 1 : S'asseoir à la place d'un de ses voisins.
La distance 2 : S'asseoir à la place du voisin de gauche de son voisin de gauche ou bien à la place du voisin de droite de son voisin de droite.
.....
La distance 6 : S'asseoir à 6 rangs de sa place initiale (On peut noter que ce déplacement n'est accessible que pour A ou pour G prenant respectivement la place de G ou de A, mais bref ... en fait on a même pas besoin de le savoir pour la suite).

Supposons que nos 7 bonshommes parcourent tous une distance différente. Etant donné qu'il n'y a que 7 distances possibles, chaque distance sera parcourue une et exactement UNE seule fois.

Ensuite on se rend compte qu'il faut que la distance totale parcourue vers la gauche soit égale à la distance totale parcourue vers la droite pour que chaque chaise soit occupée après déplacement. Cette distance vaut évidemment la distance totale / 2.

Or la distance totale vaut 0+1+2+3+4+5+6 = 21. Le fait que ce nombre soit impair est en contradiction avec l'énoncé du problème.




Pour aller plus loinSpoiler : [Afficher le message]
Notons que :

2personnes
0+1=1 est impair. En effet c'est très facile de prouver que ce problème n'a pas de solutions s'il y a 2 personnes

3 personnes
0+1+2 = 3 est impair. De même quelques dessins permettent de prouver qu'il n'y a pas de solutions pour n=3

4 personnes
0+1+2+3 = 6 est pair (A->D, B->A, C->C, D->B est une solution)

5 personnes
0+1+2+3+4 = 10 est pair (A->E, B->C, C->A, D->D, E->B est une solution)

6 personnes
0+1+2+3+4+5 = 15 est impair. Pas de solution

7 personnes : Pas de solutions

On montre ainsi facilement que si le nombre de personnes est de la forme 4n+2 ou 4n+3 il n'y a pas de solutions car la somme de tous les entiers naturels strictement inférieur au nombre de personnes est un nombre impair.
Par contre il resterait à montrer pour les nombres de la formes 4n et 4n+1 s'il existe toujours un algo de placement qui marche.

Oh, eh, de toute façon, statistiquement, sur sept couples de danse, y en a bien un qui va finir au plumard, non ?

Frank , tu peux t'intéresser sur la distance parcourue de la place de X jusqu'à celle de x en ligne droite !

heu j'édite, comment je cache la réponse? J'espère qu'en spoiler ca marchera :s

Spoiler : [Afficher le message] Considérons les "distances parcourues" comme le décalage entre le siège de monsieur et de madame. Distance : nulle si on va en face, 1 si on se décale de 1 vers la droite etc... La vraie distance sera l'hypothénuse du triangle formé par x, X et le siege en face de X. Deux distances sont identiques si le carré de ces décalages sont égaux.

La somme des distances parcourues de facon algébrique doit être nulle : au final les messieurs sont globalement en même position.

Pour être toutes différentes, les distances parcourues, en valeur absolue, doivent être 0,1,2,3,4,5,6. Donc il faut faire une somme de ces chiffres, avec des moins où on veut, qui fasse 0.
Or leur somme vaut 21, qui est impair. Quoi qu'on choisisse, le résultat sera impair (le moins ne change rien à la parité), donc non nul.

Il est donc impossible que tous aient parcouru une distance différente.

Bonjour,

Un petit schéma devrait permettre de mieux expliquer :

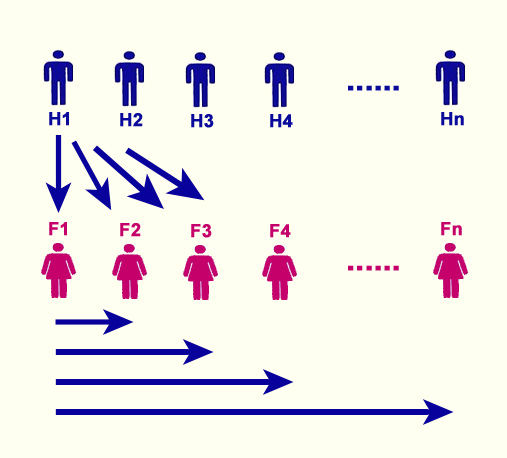
Il y a autant de distances obliques homme-femme que de distances horizontales femme-femme (ou homme-homme).

S'il y a N hommes et N femmes, alors il y a N-1 distances horizontales différentes. Donc N-1 distances obliques possibles. Ce qui signifie que parmi les N hommes qui se déplacent, il y en a au moins 2 qui parcourent la même distance.

J'espère que mon explication est claire...
Klim.

[Edit] Je confirme ton mp : j'ai réfléchi trop vite et trop stupide, en oubliant le déplacement purement vertical. Mais désolé, je n'ai pas le temps de m'y remettre, pour l'instant en tout cas.... Je regarderai la solution avec intérêt...
Klim.

Supposons qu'il puisse y avoir un cas où tous les hommes parcourent une distance différente.

Le décalage possible varie entre 0 et 6, or il y a 7 hommes donc tous les décalages doivent être effectués (0, 1, 2, 3, 4, 5 et 6).
En mettant les hommes sur l'axe des abscisses, on peut dire que les décalages peuvent être positifs ou négatifs et que leur somme doit être nulle car l'abscisse des hommes reste globalement inchangée.

Le problème c'est que quand on additionne 7 nombres dont 3 impairs, le résultat est toujours impair donc ne peut être 0.
On arrive à une impossibilité donc il y a forcément deux hommes qui ont parcouru la même distance.

Général pour n:
on range les n hommes de 1 à n et pareil pour les femmes. On dira que quand un homme au rang h va vers la femme au rang f qu'il se déplace de la valeur h-f. Comme tout homme va se déplacer, et tous d'une longueur différente, la somme des h-f est :0+1+2+...n-1, soit bien n valeurs différentes. Mais comme au final chaque homme aura trouvé une place destinataire différente, qui occupe donc tous les rangs une fois de 1 à n, c'est à dire comme au départ, la somme algébrique des déplacements doit être nulle.
Somme des valeurs absolues de tous les déplacements: n(n-1)/2.
Pour que la somme algébrique soit nulle, il faut que cette valeur soit paire.
Ce qui n'est pas le cas de 7 car7*6/2=21.

Mais on arrive à trouver une solution si n ou n-1 sont divisibles par 4.

A   B   C   D   E   F   G

f    e   d    g   c   b   a


Les Hommes vont chercher les femmes de la même lettre minuscule

Bravo nodgim