 |
#1 - 10-11-2011 22:57:44
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3222
- Lieu: Luxembourg
IIsomorphisme ?
Bonjour,
Je vous propose une petite colle qui va certainement vous distraire : il s’agit d’un problème posé par Martin Gardner dans son livre "Ha-ha" ; à l’époque, la solution (qui passe par un isomorphisme) m’avait plutôt surpris et, aujourd’hui, ce problème me revient en mémoire.
Et je suis désolé si cette colle a déjà été posée sur ce site (d’ailleurs je ne sais pas vraiment comment chercher de façon efficace s’il existe une énigme similaire ou même identique).
Voici les règles du jeu : il suffit de poser, à tour de rôle, des pièces de monnaie sur une table (comme au casino) portant les numéros 1 à 9. Peu importe qui commence. Tu déposes des pièces de 10 centimes ; moi, je dépose des pièces de 1 euro. Le premier qui couvre trois chiffres différents dont la somme est 15 gagne tout l’argent déjà déposé.
Suivons une partie : tu commences et poses une pièce sur le 7. Comme le 7 est couvert, aucun des joueurs ne peut plus y déposer de pièce. Je pose une pièce sur le 8. Au tour suivant, tu poses une pièce sur le 2 : ainsi, avec une autre pièce sur le 6, les trois chiffres couverts auront pour somme 15 et tu auras gagné. Mais je pose bien sur une pièce sur le 6. A présent, je peux gagner en jouant le 1 au tour suivant. Tu vois le danger et entraves ma victoire avec une pièce sur le 1. Je pose ma pièce suivante sur le 4. En s’apercevant que je gagnerais en jouant ensuite le 5, tu bloques ce chiffre et poses donc une pièce sur le 5. Mais je pose une pièce sur le 3 et gagne puisque 8 + 4 + 3 = 15. Tu as perdu quatre pièces.
Et voici la question : comment jouer à une partie sans jamais perdre ?
Bon courage.
Et bonne soirée.
Frank
#2 - 11-11-2011 06:45:28
- Yuka2
- Habitué de Prise2Tete
- Enigmes résolues : 48
- Messages : 31
Isomorhpisme ?
On considère qu'on commence à jouer.
Pour ne jamais perdre il faut s'assurer de bloquer toutes les combinaisons gagnantes de l'adversaire.
Si on dénombre les combinaisons gagnantes, on en trouve seulement 8 :
159
168
249
258
267
348
357
456
Les chiffres 1,3,7 et 9 apparaissent 2 fois, les chiffres 2,4,6 et 8 apparaissent 3 fois et le chiffre 5 apparait 4 fois.
Il semble judicieux de jouer le 5 en premier.
Cela bloque déjà 4 positions sur les 8.
Il reste
168
249
267
348
Cas 1 : L'adversaire joue 2
On joue 4
On bloque ainsi 2 des possibilités restantes de victoire. L'adversaire ne peut plus gagner qu'en jouant :
267
168
Or l'adversaire doit jouer absolument 6 pour nous empêcher de gagner dès le coup suivant. (car 5+4+6 = 15)
On répond ainsi en jouant 7.
L'adversaire ne peut plus gagner qu'en misant sur le tirage 168.
Peu importe qu'il joue 1 ou 8 au coup suivant, on le bloque définitivement en jouant le numéro restant juste après.
Cas 2 (quasi similaire) : L'adversaire joue 8
On joue 4
On bloque ainsi 2 des possibilités restantes de victoire. L'adversaire ne peut plus gagner qu'en jouant :
267
168
Or l'adversaire doit jouer absolument 6 pour nous empêcher de gagner dès le coup suivant. (car 5+4+6 = 15)
On répond ainsi en jouant 1.
L'adversaire ne peut plus gagner qu'en misant sur le tirage 267.
Peu importe qu'il joue 2 ou 7 au coup suivant, on le bloque définitivement en jouant le numéro restant juste après.
Cas 3 : L'adversaire joue ni 2 ni 8 :
On joue le 2.
Il ne reste plus que :
348
168
L'adversaire est obligé de jouer 8 (car 5+2+8 =15)
Au troisième coup on l'empêche de gagner ( ie, on joue 3 s'il a 4 et 8, 4 s'il a 3 et 8, 1 s'il a 6 et 8 et 6 s'il a 1 et 8, et 1,3,4 ou 6 s'il a le 7 ou le 9 en plus du 8).
Il ne lui restera donc plus qu'une combinaison gagnante pour laquelle il n'aura que le chiffre 8 et aucun des deux autres.
Peu importe son 3ème coup car au quatrième on pourra toujours le bloquer définitivement.
J'imagine qu'un raisonnement de ce type doit marcher aussi si on suppose qu'on ne commence pas à jouer.
En distinguant 2 cas : S'il joue le 5 en premier (difficile) et s'il ne joue pas le 5 en premier (moins difficile)
#3 - 11-11-2011 07:51:56
- NickoGecko
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1821
Iomorphisme ?
Bonjour,
Merci de proposer ce sujet, j'aime bien aussi Martin GARDNER
(Le paradoxe du pendu, 123 l'infini etc ...)
Dans le jeu proposé ici :
Il y a 8 triplets d'entiers distincts entre 1 à 9 dont la somme vaut 15, i.e. 8 manières (au final, sans tenir compte de l'ordre des choix par coup) de déposer des pièces sur les cases et de gagner :
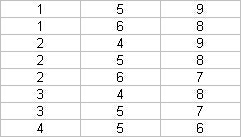
(On y retrouve bien le 8, 4, 3 de l'exemple, ouf !)
On peut trier par ordre croissant l'occurence de chaque nombre parmi ces 8 triplets.
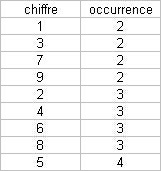
On remarque que quatre entiers impairs apparaissent 2 fois (1,3,7,9)
quatre autres, pairs, apparaissent 3 fois (2,4,6,8)
et un seul, le 5, apparait 4 fois.
Ce qui devrait correspondre aux cases à jouer "en priorité"
En essayant de les regrouper par séquences, j'ai retrouvé l'arrangement suivant sur un carré de 3x3, dont la somme des lignes et des colonnes et des diagonales vaut 15.
On retrouve en fait un "carré magique" :
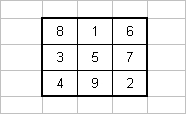
Suivons la partie de l'énoncé en imaginant jouer au "morpion" sur cette grille :

L'isomorphisme signifie que ce jeu avec des pièces et 9 cases s'apparente au jeu de "morpion" bien connu, dont l'objectif est d'aligner trois cases horizontalement, verticalement ou en diagonale en transposant les 9 cases vers un carré de 3x3 ci-dessus (aux rotations et permutations près) .
On sait que ce jeu peut être gagnant, ou au moins "partie nulle"
Très intéressant, merci !
A bientôt
Il aurait pu pleuvoir, con comme il est ! (Coluche)
#4 - 11-11-2011 07:58:51
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
isimorphisme ?
A joue 7, B doit jouer 8 pour contrer.
A joue 6, B doit jouer 2 pour contrer 7+6+2=15 ou 9 pour contrer 9+6=15: fin car quel que soit le choix de B, A gagne en prenant l'autre option.
Notons que le 1er joueur gagne toujours.
#5 - 11-11-2011 08:30:23
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 5,997E+3
Isomoorphisme ?
Il faut commencer par jouer le 5 qui ouvre une possibilité avec chacun des autres nombres
5-1-9
5-2-8
5-3-7
5-4-6
Suivant la réponse, il faut jouer un des 4 nombres qui ouvre deux possibilités de jeu (2 4 6 8 )
S'il répond 1, je dis 2 , il est alors obligé de dire 8, je le bloque à 6
Fourchette ! il doit me bloquer sur 5-6-4 et 2-6-7 en même temps...
Le raisonnement est le même quelle que soit sa réponse. Au premier coup je me donne 4 options, au second , un nombre qui en laisse 3, au troisième coup, je m'offre 2 possibilités de gagner.
Même si on commence chacun son tour, je gagne des euros et toi des centimes 
#6 - 11-11-2011 10:19:35
- Clydevil
- Expert de Prise2Tete
- Enigmes résolues : 29
- Messages : 914
- Lieu: Seahaven island
Isomrphisme ?
He oui il me semble l'avoir déjà croisé un jour celui la, une très belle solution qui illustre parfaitement qu'un même problème peut être vu de point de vu totalement différent.
C'est un morpion:
6 1 8
7 5 3
2 9 4
Je pense que ce n'est pas impossible de le trouver tout seul car a priori si on passe l’étape de la cuisine on va lister toutes les possibilités de faire 15 et tenter de voir ça sous forme de graphe, et si on a l’étincelle pour le représenter de manière compacte, ho le beau carré!
#7 - 11-11-2011 23:11:09
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
isomorohisme ?
Ce jeu est équivalent à un tic-tac-toe sur un carré magique de côté 3 et on sait que ce jeu est nul si chacun joue au mieux 
Vasimolo
#8 - 13-11-2011 21:58:49
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3222
- Lieu: Luxembourg
Isomoorphisme ?
Bonsoir,
Cette énigme ne semble pas avoir beaucoup de succès et, comme il ne reste que deux petites heures, on va passer directement à la solution.
Nickogecko, Clydevil et Vasimolo connaissaient l'astuce (mais je pense qu'il faut l'avoir déjà vu). Yuka2, nodgim et gwen27 ont beaucoup bossé et esquissé une solution sans connaitre cette astuce. Merci à vous tous pour vos réponses.
L'astuce consiste à voir que la stratégie de ce jeu est mathématiquement équivalente à celle du tictactoe. Comme il existe huit combinaisons de trois chiffres dont la somme est 15, on peut établir un carré magique (sauf erreur de ma part, ce carré est unique aux rotations et symétries prés):
6 1 8
7 5 3
2 9 4
Vous devinez la suite: si deux adversaires jouent parfaitement au tictactoe (que vous connaissez tous), alors la partie est indécise. Mais en jouant au jeu décrit sans se rendre compte que l'on joue en réalité au tictactoe, on part évidemment avec un gros handicap. Si on connait cette astuce, on est en position de force pour pouvoir tendre des pièges (comme les fourchettes que vous avez évoquées). Deux adversaires qui connaissent cette astuce feront bien sur match nul à chaque fois (mais l'histoire ne dit pas comment, dans ces cas, on se partage la cagnotte  ). ).
Personnellement, l'isomorphisme m'a toujours étonné: résoudre un problème en le transformant en un autre qui lui est isomorphe est impressionnant. Je sais que le fameux théorème des quatre couleurs démontré en 1976 prouva simultanément des douzaines d'autres conjectures mathématiques isomorphes à ce théorème. Et, si je ne dis pas d'ânerie, une étape de la longue démonstration du théorème de Fermat-Wiles en 1994 est basée sur la démonstration de la conjecture de Shimura-Taniyama-Weil par Andrew Wiles, isomorphe à cette étape (c'était un peu plus compliqué que de jouer au tictactoe  ). ).
J'espère que mon petit speech sur l'isomorphisme vous aura détendu. Et je vous dis à bientôt pour une énigme un peu plus conventionnelle.
Bonne soirée à tous.
Frank
#9 - 13-11-2011 23:12:48
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Isomorphhisme ?
Je ne connaissais pas mais j'ai vite fait le parallèle avec le Tic-Tac-Toe 
Mais bon 
Vasimolo
#10 - 14-11-2011 00:26:06
- Psykotaker
- Habitué de Prise2Tete
- Enigmes résolues : 0
- Messages : 28
- Lieu: Université Paul Verlaine
iqomorphisme ?
@Francky,
La démonstration du théorème des 4 couleurs fait toujours polémique car ça résolution à été entièrement fait par ordinateur
D'après excellent livre la symphonie des nombres premier (de Marcus du Sautoy), Kenneth Appel et Wolfgang Haken ont "juste" démontré qu'il n'existe qu'un peu moins de 1500 schémas de cartes possible et les ont codé puis dessiner par ordinateur (simplification très grossière je vous l'accorde)
Quand les choses deviennent trop compliquées, il est parfois normal [...] de se demander : ai-je posé la bonne question ?
#11 - 14-11-2011 00:54:41
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3222
- Lieu: Luxembourg
Isomorpihsme ?
@Vasimolo: Alors un grand bravo si tu as vu le rapprochement avec le jeu tictactoe sans l'avoir vu avant: je suis vraiment impressionné.
@Psykotaker: Je ne savais pas que le théorème des quatre couleurs avait été démontré par ordinateur, ce qui implique que tous les cas de figures ont dûs être examinés (et d'être sûr que c'était bien le cas). Pour moi, un des charmes des maths est le côté "preuve absolue" (où, contrairement à la physique, on ne se contente pas de constater qu'une "loi fonctionne"), d'où sans doute cette polémique. Merci aussi pour les références du bouquin (j'adore ce type de lecture).
Bonne soirée.
#12 - 14-11-2011 11:21:30
- Clydevil
- Expert de Prise2Tete
- Enigmes résolues : 29
- Messages : 914
- Lieu: Seahaven island
isomorphismz ?
Pour moi, un des charmes des maths est le côté "preuve absolue" (où, contrairement à la physique, on ne se contente pas de constater qu'une "loi fonctionne"), d'où sans doute cette polémique.
Oui c'est vrai mais imaginons que tu veuille démontrer une propriété d'une suite d'entiers, et que tu trouves qu'à partir du terme U(5) (le 5eme je veux dire) tu peux facilement écrire une relation de récurrence qui transmet cette propriété aux termes suivants. Tu va vérifier cette propriété pour U5 et pour les U0,..,U4 avant comme cas particulier et déclarer que tu as une preuve, qui est totalement rigoureuse et absolue n'est ce pas?
Maintenant imagine la même chose mais avec ta relation de récurrence que tu trouve a partir de U(2^64), qu'est ce que tu fais? tu ne considèrerais plus ceci comme preuve absolue si tu considères les 2^64 cas particuliers par ordinateur?
C'était bien sur ceci le travail de démonstration du théorème des 4 couleurs, réussir a construire un ensemble fini de cas tel que si tout dans cette ensemble est faisable alors le théorème des 4 couleurs s'applique également à n'importe quel graphe planaire dans leur famille infinie. La ou ca polémique c'est que bien sur il faut faire confiance à la vérification des cas particuliers qui n'a aucune accessibilité humaine, on se contente de vérifier la réduction de cas, le programme lui même, et faire confiance en sa correcte application sur les données.
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum










