|
#1 - 12-11-2011 10:11:14
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
#2 - 12-11-2011 10:46:09
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
Gâteau 4
Au premier regard, j'en étais à douter de l'existence de ce point...
C'est l'intersection de 2 droites.
Pour la 1ere droite: On trace une parallèle à AD distante de BC et une parallèle à BC distante de AD. Le point d'intersection de ces 2 parallèles et le point d'intersection des prolongements de AD et BC sont 2 points de la 1ère droite.
Faire la même chose pour la seconde droite avec AB et CD.
#3 - 12-11-2011 10:49:00
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
hâteau 44
Il y a une solution géométrique sans aucun calcul 
Vasimolo
#4 - 12-11-2011 11:08:34
- Psykotaker
- Habitué de Prise2Tete
- Enigmes résolues : 0
- Messages : 28
- Lieu: Université Paul Verlaine
âGteau 44
A tout hasard, O ne serait pas tout simplement le centre de gravité de ABCD ?
Quand les choses deviennent trop compliquées, il est parfois normal [...] de se demander : ai-je posé la bonne question ?
#5 - 12-11-2011 11:21:53
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Gteau 44
Le hasard ne fait pas toujours bien les choses 
Vasimolo
#6 - 12-11-2011 11:52:25
- TiLapiot
- Expert de Prise2Tete
- Enigmes résolues : 16
- Messages : 852
- Lieu: au terrier ;^)
fâteau 44
Ah un gâteau........
C'est le sommet commun à tous les triangles 
Au fait, les distances AB, AD, DC, BC sont-elles obligatoirement des valeurs entières ? (oupsss!)
#7 - 12-11-2011 12:47:05
- shadock
- Elite de Prise2Tete
- Enigmes résolues : 39
- Messages : 3334
gâtrau 44
Il se trouve sur le barycentre du gâteau non ?
Je ferai le dessin plus tard.
(On prend le milieu de chaque côté du gâteau, et on trace les deux droites passant par les milieux opposés, elles se coupent en un point O.)
Shadock 
"L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
#8 - 12-11-2011 12:51:59
- Klimrod
- Elite de Prise2Tete
- Enigmes résolues : 40
- Messages : 4050
- Lieu: hébesphénorotonde triangulaire
Gâtea 44
Bonjour,
Vasimolo a écrit:Mais où est le point O ?
Ca me rappelle une histoire drôle :
Désolé, je n'ai pas pu m'empêcher... ------->[]
[Edit] Pour être plus sérieux, le point O devrait être sur le centre de gravité, non ? En fait, je n'en suis pas très sûr...
J'ai tant besoin de temps pour buller qu'il n'en reste plus assez pour bosser. Qui vit sans folie n'est pas si sage qu'il croit.
#9 - 12-11-2011 12:57:37
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
Gâtaeu 44
Bon j'ai donné une soluce géométrique, je ne sais pas s'il y a plus simple.
#10 - 12-11-2011 15:21:08
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
gâyeau 44
@Nodgim
Je ne pense pas que ta construction soit juste !
Vasimolo
#11 - 12-11-2011 16:27:51
- esereth
- Professionnel de Prise2Tete
- Enigmes résolues : 49
- Messages : 176
Gâteeau 44
Je ne sais pas si cela répond entièrement à la question.
J'ai trouvé ça dans un vieux pb (gâteau 6). Il est facile de montrer que ça donne une solution Puisque B et D sont équidistants de (AC), les triangles ABC et ADC ont même aire.
Si on prend O milieu de [AC], les médianes[OB] et [OD] coupent les deux précédents triangles en deux parties égales.
D'où le résultat escompté dans ce cas particulier.
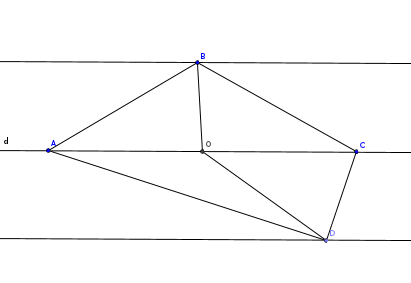
Maintenant s'il faut montrer que la condition est nécessaire pour pouvoir réussir une construction, je n'ai pas trouvé.
#12 - 12-11-2011 16:59:13
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
gâyeau 44
Une construction d'esereth pour un cas particulier de gâteau 
Existe-t-il d'autre gâteaux pour lesquels le partage est possible ???
Vasimolo
#13 - 12-11-2011 18:05:42
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
Gâteaau 44
C'est vrai que j'ai seulement réalisé le partage correct 2 à 2 (ceux des cotés se faisant face) mais pas les 4 ensemble.
Aussi, j'en reviens à mon idée première en disant que seuls des cas particuliers peuvent marcher, et que ça ne marche pas dans le cas général.
ça marche avec le losange, mais pas avec le parallélogramme.
#14 - 12-11-2011 20:11:41
- TiLapiot
- Expert de Prise2Tete
- Enigmes résolues : 16
- Messages : 852
- Lieu: au terrier ;^)
Gâtea 44
J'ai commencé avec de la pâte feuilletée (lol)...
...avec un quadrilatère tracé sur une feuille A4, mais ne trouvant pas de construction systématique ("abordable"), j'ai ensuite essayé de mouliner sous EXCEL...
Même si ma construction sur papier ne donnait rien, mais j'ai qd même constaté que O semblait le milieu de AC.
En imposant le point A en (0;0), et le point B en (5;0), zou la moulinette pour trouver les points C, D et O (milieu de AC)...
J'ai (ahem... Excel a) trouvé plusieurs scénarios possibles, dont en voici un :

#15 - 13-11-2011 00:02:57
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
gâtrau 44
Un petit bilan et j'ajoute un indice dans le message initial .
@Nodgim : essaie sur des exemples où tu sais faire smile
@Psykotaker et Klimrod : vous avez raison de douter , O n'est pas le centre gravité ( en général ) .
@Shadock : non ce n'est pas le point d'intersection des médianes .
Esereth et TiLapiot : vous avez la réponse , il ne manque plus que la preuve smile
Vasimolo
PS : j'ajouterai peut-être un peu de temps si on me le demande poliment 
Personnellement je ne suis pas fan des sujets qui traînent en aveugle sur une semaine ou plus .
#16 - 13-11-2011 09:09:24
- halloduda
- Professionnel de Prise2Tete
- Enigmes résolues : 24
- Messages : 495
- Lieu: Ardèche
GGâteau 44
Oui, le point O n'existe que si le gâteau est un parallélogramme.
En effet, aire(AOD)=aire(AOB) exige O sur la demi-droite qui relie le point A au milieu de BD.
(les distances de O à AB et AD sont dans la proportion AD/AB).
De même, O est sur la demi-droite qui relie le point C au milieu de BD.
Sauf forme particulière, O est donc le milieu de BD.
De même, il est le milieu de AC.
Pour satisfaire toutes ces conditions, les milieux de BD et de AC doivent être confondus.
ABCD est alors un parallélogramme, O en est le centre.
EDIT suite à note de Vasimolo
Forme particulière évoquée plus haut : (A, O et C alignés)
Alors, il suffit que les distances de B et D à AC soit égales.
Ou que le milieu de BD soit sur AC (c'est la même chose).
#17 - 13-11-2011 10:15:58
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Gâteau 4
C'est l'idée , halloduda , mais la conclusion n'est pas bonne 

Vasimolo
#18 - 13-11-2011 18:59:09
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Gâtaeu 44
J'ai ajouté un deuxième indice 
Vasimolo
#19 - 13-11-2011 21:21:10
- looozer
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 697
- Lieu: Belgique
gâteay 44
Il faut qu'une diagonale (au moins) passe par le milieu de l'autre.
Ce milieu est alors le point O recherché. => j'y retourne j'aurais dû vérifier 
Voilà mieux :
Il faut qu'une diagonale passe par le milieu de l'autre.
Le milieu de la première est alors le point O recherché.
Beaucoup moins simple qu'il n'y paraît ce gâteau (et merci pour les indices qui m'ont motivé à me relancer alors que j'avais lâchement laissé tomber  ) )
#20 - 13-11-2011 22:49:00
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
âteau 44
Non looozer 
La condition nécessaire et suffisante d'existence doit pouvoir se lire sur mon dernier dessin , après il faut le prouver ...
N'hésite pas à utiliser le 2ème indice 
Vasimolo
#21 - 13-11-2011 23:20:17
- looozer
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 697
- Lieu: Belgique
Gâteau 4
Bizarre, pourtant ça marche chez moi :
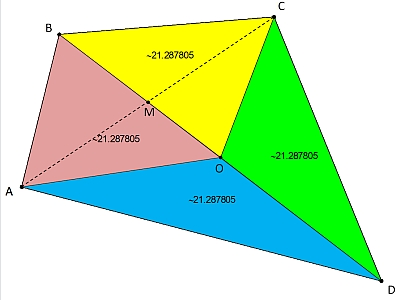
Je m'en vais rédiger une petite preuve...
Si O est le point tel que ABO et BCO ont la même aire et sachant que BO est une base commune à ces deux triangles, les hauteurs relatives à BO dans ces deux triangles doivent être égales (et parallèles).
Elles déterminent donc un parallélogramme dont une diagonale est AC et l'autre BO. La droite BO doit donc forcément passer par le milieu M de AC.
Dans le quadrilatère ABCD, O doit donc se trouver sur BM.
Par analogie, il doit aussi se trouver sur DM. O ne peut donc être que M lui-même.
A ce stade ABO et BCO ont même aire, ADO et DCO également.
Pour que les 4 aient la même aire, il faut encore que CN et AN (N étant le milieu de BD) passent également par M, ce qui arrivera si N appartient à AC.
Je ne suis pas très simple, sans doute, mais je n'ai pas mieux pour ma défense ;-)
PS : J'ai modifié mon dessin pour qu'il corresponde à l'énoncé et à mes explications.
#22 - 13-11-2011 23:24:54
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Gâtteau 44
En fait tu as raison , c'est une autre façon d'exprimer ce que j'avais en tête , j'attends ta démo 
Vasimolo
#23 - 14-11-2011 10:54:41
- Zindy
- Professionnel de Prise2Tete
- Enigmes résolues : 48
- Messages : 104
GGâteau 44
Si, dans un quadrilatère ABCD, deux sommets opposés (par exemple B et D) sont à égale distance de la diagonale formée par les deux autres sommets (dans notre exemple, la diagonale AC), alors on peut trouver très facilement le point O, il sera au milieu de la diagonale, donc tel que AO=OC.
Pourquoi ça marche ? Eh bien O étant au milieu de la diagonale, les triangles AOB et BOC ont une base de même longueur (AO=OC), ils ont la même hauteur h1, donc la même aire (base x hauteur/2). De même, les triangles AOD et DOC ont une base de même longueur (AO=OC), ils ont la même hauteur h2, donc la même aire (base x hauteur/2).
Or notre quadrilatère a ses deux sommets B et D à égale distance de la diagonale AC, donc les deux hauteurs h1 et h2 sont égales de part et d'autre de la diagonale du quadrilatère. Les aires des quatre triangles, donc des quatre parts de gâteau, sont égales, et tout le monde est content, sauf les gourmands qui aiment bien avoir la part la plus grosse...!
#24 - 14-11-2011 11:22:54
- NickoGecko
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1821
Gâteau 444
Il aurait pu pleuvoir, con comme il est ! (Coluche)
#25 - 14-11-2011 16:55:52
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 5,996E+3
hâteau 44
Pour que les triangles aient la même aire, il faut que les hauteurs issue des sommets opposés à leur face commune soient de même longueur.
Le milieu de [BD] appartient donc à la droite (OC) ainsi qu'à la droite (OA)
Idem pour le milieu de [AC] qui appartient donc à la droite (OB) ainsi qu'à la droite (OD)
Pour que ces deux conditions soient réunies, il faut que le milieu d'une des diagonales (au moins) appartienne à l'autre diagonale. Le point O est alors le milieu de cette seconde diagonale.
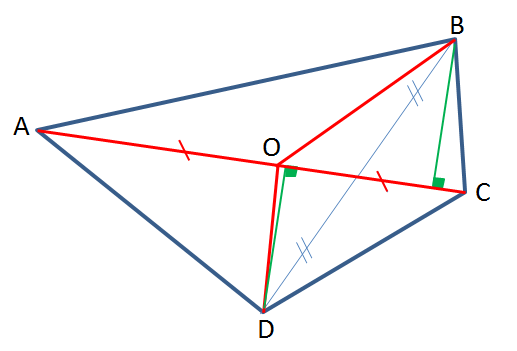
En espérant être clair...
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum