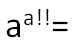|
#1 - 27-10-2014 18:57:55
- PRINCELEROI
- Elite de Prise2Tete
- Enigmes résolues : 33
- Messages : 1274
La machnie
La machine;vous y mettez un nombre qui est un entier naturel non nul et il en ressort un nombre.
Elle utilise 5 symboles qui ont un sens mathématique et le dernier est obligatoirement =
Exemple: a x a ! =
Les règles de priorités
1°) les fonctions ( ici les factorielles ) .
2°) les puissances .
3°) les multiplications et les divisions .
4°) les additions et les soustractions .
5°) les autres choses .
Ici si a=1 la machine donne 1
Si a=2 le résultat est 4
Si a=3 cela donne 18
Aucun autre nombre n'est préexistant dans la machine.
Vous ne pouvez utiliser que des choses existantes dans les mathématiques.
Pas de fonction perso smile
Vous devez inventer une machine qui donne 1 quand a=1,4 quand a=2 et le plus grand nombre possible quand a=3.
Que le meilleur gagne!
#2 - 27-10-2014 19:20:11
- SabanSuresh
- Elite de Prise2Tete
- Enigmes résolues : 45
- Messages : 1951
- Lieu: Paris
la macjine
Bonsoir,
Quand vous dites "1°) les fonctions" et "vous ne pouvez utiliser que des choses existantes dans les mathématiques", on peut utiliser les flèches de knuth par exemple ?
Si on peut les utiliser et qu'une double flèche est compté comme deux caractères, j'ai :
a↑↑a=
Ça donne f(1) = 1, f(2) = 2^2 = 4 et f(3) = 3^3^3 = 3^27 = 7625597484987.
Si une double flèche est compté pour un caractère et une triple flèche pour deux caractère, j'ai :
a↑↑↑a=
Ça donne f(1) = 1, f(2) = 2↑↑2 = 2^2 = 4 et
f(3) = 3↑↑3↑↑3 = 3↑↑(3^27) = 3↑↑7625597484987 = 3^3^3^3^3^3^3^3^3 ...
avec 7625597484987 fois le nombre 3.
Après si les opérateurs triple flèche, quadruple flèche, quintuple flèche compte pour un seul caractère car ils correspondent à un seul opérateur, on peut aller très très loin.
Voilà.
#3 - 27-10-2014 19:46:51
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 5,996E+3
la macgine
par exemple :
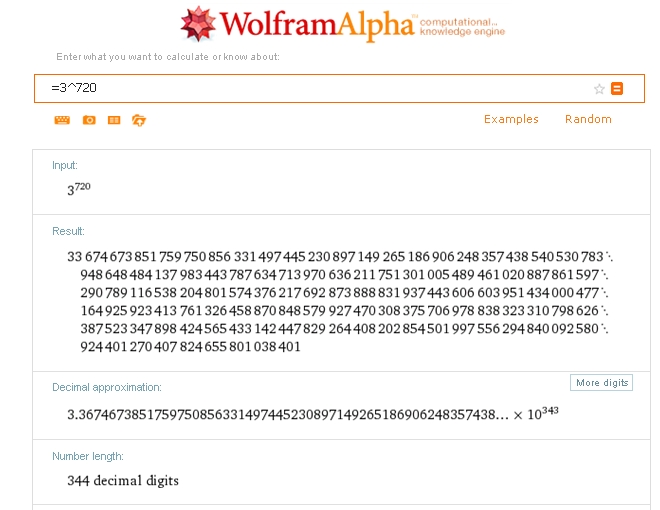
a^a!!!= ???
Wolfram dit que c'est.... euh beaucoup 
EDIT non, tu sous-entends "a" inclus dans les 5 ?
#4 - 27-10-2014 20:11:47
- Sydre
- Professionnel de Prise2Tete
- Enigmes résolues : 15
- Messages : 245
la machinr
Je propose 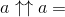
Le résultat pour 3 est 7625597484987

#5 - 27-10-2014 21:52:38
- cogito
- Expert de Prise2Tete
- Enigmes résolues : 48
- Messages : 593
L machine
Bonsoir 
Là comme ça je dirais a ^ a ! =
Pour a = 1 on a 1 ^ 1 ! = 1 ^ 1 = 1.
Pour a = 2 on a 2 ^ 2 ! = 2 ^ 2 = 4.
Pour a = 3 on a 3 ^ 3 ! = 3 ^ 6 = 729.
Mais ça ressemble trop à l'exemple donné, je vais voir si je trouve mieux.
Il y a sûrement plus simple.
#6 - 27-10-2014 21:56:29
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
La machhine
Je propose a^a!=
Où 3^3!=729
#7 - 27-10-2014 22:13:05
- NickoGecko
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1821
la machune
Bonjour
Quelque chose comme :
(3a-2) + (a-1)(a-2)((((((((((a!)!)!)!)!)!)!)!)!)!)!)! =
encore plus grand ? je vais user la touche "!" !
Edit : ridicule ! > voir plus bas !
A suivre !
A+
Il aurait pu pleuvoir, con comme il est ! (Coluche)
#8 - 27-10-2014 22:26:31
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3222
- Lieu: Luxembourg
aL machine
Avec cinq symboles, pour l'instant, je n'ai pas trouvé mieux que: a!^a!! =
1!^1!! = 1^1 = 1 2!^2!! = 2^2 = 4 3!^3!! = 6^720 = 1,8575.10^560
#9 - 27-10-2014 23:15:35
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
ka machine
Faut-il obligatoirement marquer le symbole "x" pour une multiplication, le symbole "^" pour une puissance ?
il y a la formule : a! (puissance mais LateX ne marche pas) a! qui donne 46 656.
#10 - 28-10-2014 06:20:39
- PRINCELEROI
- Elite de Prise2Tete
- Enigmes résolues : 33
- Messages : 1274
La macihne
gwen:oui
nicko:5 symboles
golgot:c'est petit
titou:oui, a fait parti des symboles
saban et sydre semble avoir les "nuts" terme au poker qui signifie avoir le meilleur jeu possible mais içi le jeu de mot est possible!
#11 - 28-10-2014 09:54:40
- godisdead
- Expert de Prise2Tete
- Enigmes résolues : 22
- Messages : 747
ma machine
a^a !! =
Je n'arrive pas à utiliser latex pour faire a puissance a ...
#12 - 28-10-2014 11:44:22
- NickoGecko
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1821
la machinz
Il aurait pu pleuvoir, con comme il est ! (Coluche)
#13 - 28-10-2014 12:14:00
- FRiZMOUT
- Verbicruciste binairien
- Enigmes résolues : 49
- Messages : 2218
aL machine
Je propose : a ↑↑ a =
Ce qui donne 7625597484987 pour a = 3.
#14 - 28-10-2014 14:20:00
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1968
la machune
Allons y donc.
Je propose d'utiliser les puissances iterées de Knuth, avec a↑↑a= (qui rappellons le correspond à a^(a^(a^...))) répété autant de fois que le terme de droite, soit a fois)
1↑↑1 = 1
2↑↑2 = 2^2 = 4
3↑↑3 = 3^(3^3) = 3^27 = 7625597484987
Voir mieux encore a ↑a a=
↑a correspond à une iteration de la puissance de Knuth...
Du coup
1 ↑1 1 = 1^1 = 1
2 ↑2 2 = 2↑↑2 = 2^2 = 4
Et enfin 3 ↑3 3 = 3↑↑3↑↑3 = 3^3^3... 7625597484987 fois
#15 - 28-10-2014 15:08:00
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
La macihne
Ce n'était pas ma question. Est-ce que le symbole "^" est obligatoire pour une puissance ? Est-ce que le symbole "x" est obligatoire pour une multiplication ?
#16 - 28-10-2014 17:08:53
- PRINCELEROI
- Elite de Prise2Tete
- Enigmes résolues : 33
- Messages : 1274
la machune
godisdead:tu as 6 symboles.
Nicko:il faut écrire la fonction.
titou:oui,il faut écrire la fonction.
FRIZMOUT:j'en suis là aussi.
scarta:d'accord pour la partie une mais qu'est le a a de la deux?
#17 - 28-10-2014 17:28:31
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 5,996E+3
L machine
Bof, je n'ai que a^a!=
729, c'est beaucoup moins...
#18 - 28-10-2014 17:39:52
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1968
#19 - 28-10-2014 17:50:14
- PRINCELEROI
- Elite de Prise2Tete
- Enigmes résolues : 33
- Messages : 1274
la mzchine
gwen:c'est peu
scarta:j'y vois 6 symboles minimum pour une écriture non latex et ma machine ne comprend pas le latex 
#20 - 28-10-2014 17:58:46
#21 - 28-10-2014 22:19:59
- PRINCELEROI
- Elite de Prise2Tete
- Enigmes résolues : 33
- Messages : 1274
La mmachine
scarta:a \uparrow^a a = je compte 6 symboles
#22 - 28-10-2014 22:35:36
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
La machin
a^a!=
donne 729 pour a=3
y a mieux ?
#23 - 28-10-2014 23:14:53
- fix33
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1198
- Lieu: Devant un clavier depuis 1748
La machiine
Salut !
Je ne suis pas sûr d'avoir tout compris, mais je propose !
a!!! =
Soit :
- 1 donne 1
- 2 donne 2
- 3 donne à peu près 2,6. 10^1746
Est-ce que je déraille ? Spoiler : [Afficher le message] Il semble que oui ! 
Bon... Puisque la fonction prime sur la puissance, je propose :
a!!^a =
Soit :
- 1 donne 1
- 2 donne 4
- 3 donne 373.248.000
A+
Je ne vien sur se site que pour faire croir que je suis treise intélligens.
#24 - 29-10-2014 01:43:31
- shadock
- Elite de Prise2Tete
- Enigmes résolues : 39
- Messages : 3334
la maxhine
EDIT : C'est j'avais mal lu donc finalement tout est bon !
On note > la flèche de Knuth
a>>a marche dans les trois cas et pour a=3 on a 7625597484987
Shadock 
"L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
#25 - 29-10-2014 06:16:26
- PRINCELEROI
- Elite de Prise2Tete
- Enigmes résolues : 33
- Messages : 1274
La machinne
titou:il y a mieux
shadock:pas mieux pour 3 et la même opération pour 1 et 2 donne le bon résultat!
fix:pour a=2 la machine doit sortir 4
Mots clés des moteurs de recherche
|
 |
|
Prise2Tete
Forum
Statistiques
Liste des membres
Hall of Fame
Contact
|

 Accueil
Accueil
 Forum
Forum







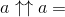
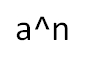
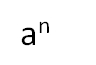 sont-ils admis ?
sont-ils admis ?