 |
#1 - 24-02-2012 15:01:06
- Promath-
- Elite de Prise2Tete
- Enigmes résolues : 18
- Messages : 1416
- Lieu: Au fond de l'univers
Concours Griego 1a∓2.
Un promath- actif dans un forum actif
#2 - 24-02-2012 15:38:46
- halloduda
- Professionnel de Prise2Tete
- Enigmes résolues : 24
- Messages : 495
- Lieu: Ardèche
Concours Girego 1&2.
1
3.33 cm
Par homothétie, le segment a pour longueur [latex]\frac432.50[/latex]=3.33 cm
EDIT Je me suis planté
2
6.92 cm
La dernier côté a pour longueur 6.92 cm
(Geogebra)
#3 - 24-02-2012 16:40:41
- fred101274
- Professionnel de Prise2Tete
- Enigmes résolues : 48
- Messages : 163
- Lieu: devant mon écran
Concours Griego 1&2..
Je suppose que ce n'est pas parallèles entre elles mais bien perpendiculaires entre elles...
Quels sont exactement les segments égaux de longueur 5?
Merci.
Pour le problème 1, sur base de tes informations, je trouve 3.383883476 cm.
J'ai pris le centre du cercle comme origine du repère, j'ai trouvé l'équation du demi-cercle, des deux tangentes, les coordonnées des points d'intersections utiles et voilà...
Pour le problème 2, la réponse est de 6.921597417 cm.
Au centre, il y a un angle de 360° découpé en 3. Je trouve la première partie grâce aux longueurs des côtés du premier triangle (Pythagore généralisé ou Al Kashi). Je fais de même pour la deuxième partie, j'en déduis donc la troisième partie. J'utilise toujours le même théorème pour trouver le côté manquant...
a² = b² + c² - 2bc cos (angle)
On n’est jamais très fort pour ce calcul...
#4 - 24-02-2012 17:16:51
- masab
- Expert de Prise2Tete
- Enigmes résolues : 44
- Messages : 971
Concours Greigo 1&2.
Griego 1
Je suppose que les tangentes sont perpendiculaires...
Réponse : 3,4
En effet on note [latex]a[/latex] l'angle situé à gauche de la figure.
On a [latex]\sin a=\frac{1}{3}[/latex] d'où [latex]\cos a=\frac{2\sqrt{2}}{3}[/latex] et [latex]\tan a=\frac{1}{2\sqrt{2}}[/latex]
La longueur cherchée est donc égale à
[TeX]2.5+2.5*\tan a =2.5+\frac{2.5}{2\sqrt{2}} = 3.383883...[/TeX]
Griego 2
Réponse : 6,92 cm
Il suffit d'appliquer la relation d'Al-Kaschi à chacun des 3 petits triangles, en prenant à chaque fois l'angle dont le sommet est à l'intérieur du grand triangle.
On note u,v,w les angles au centre. On a
[TeX]64=25+16-40*\cos u[/latex] d'où [latex]\cos u=-\frac{23}{40}[/TeX]
[TeX]36=9+16-24*\cos v[/latex] d'où [latex]\cos v=-\frac{11}{24}[/TeX]
On en déduit [latex]u=2.18340047...[/latex], [latex]v=2.0469153...[/latex] d'où [latex]w=2\pi-u-v=2.0528694...[/latex]
Finalement la longueur cherchée c est donnée par
[TeX]c^2=25+9-30*\cos w=47.90851[/TeX]
donc [latex]c=6.9215974...[/latex]
#5 - 24-02-2012 17:17:08
- Promath-
- Elite de Prise2Tete
- Enigmes résolues : 18
- Messages : 1416
- Lieu: Au fond de l'univers
Concourrs Griego 1&2.
Fred: Le segment fait 5 cm,puis il y a le demi-cercle.
Pour le 2, il me faut une démarche de résolution! 
Un promath- actif dans un forum actif
#6 - 24-02-2012 19:00:48
- Azdod
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 763
- Lieu: In this universe ... !!
Cocnours Griego 1&2.
2- Théorème d'Al kashi a plusieurs reprises nous donne : 6,9216 cm
"Zero is where everything starts ! Nothing would ever be born if we didn't depart from there"
#7 - 24-02-2012 19:34:13
- DeepSpeedou2.5
- Habitué de Prise2Tete
- Enigmes résolues : 28
- Messages : 17
- Lieu: Chez Les Bretons !
#8 - 24-02-2012 19:42:42
- gilles355
- Professionnel de Prise2Tete
- Enigmes résolues : 49
- Messages : 421
Concours Griego 11&2.
Exo 1: (Niveau 3ème)
http://www.prise2tete.fr/upload/gilles355-EXO1.jpg
On sait que DB=2,5 et que (DB) perpendiculaire à (AE) car (AE) est tangent au cercle de rayon DB.
(DB) et (EC) sont perpendiculaires à (AE) donc (DB)//(EC).
Dans le triangle AEC on peut donc utiliser thalès donc on a :
AB/AC=DB/EC
EC= ACxDB/AB
EC= 12,5x2,5/10 = 3,125.
Exo 2: (Niveau 1ère S)
http://www.prise2tete.fr/upload/gilles355-Exo2.jpg
Ici il faut utiliser le théorème d'Al Kashi (généralisation de pythagore dans les triangles non rectangle)
Calcul de Â: 6²=3²+4²-2x3x4xcos  d'où cos Â= (6²-3²-4²)/(-2x3x4)
cos Â= -11/24 donc Â= Acos (-11/24)
Calcul de l'angle B: 8²=5²+4²-2x5x4xcos B d'où cos B= (8²-5²-4²)/(-2x5x4)
cos B= -23/40 donc B= Acos (-23/40)
Calcul de l'angle C: A+B+C=360° donc C=360-A-B
Calcul du côté manquant que l'on note x:
x²= 5²+3²-2x3x5xcos C
x²= 34 - 30 cos (360-Acos(-11/24)-Acos(-23/40))
x= racine carré (34-30 cos (360-Acos(-11/24)-Acos(-23/40)) )
la valeur environ de ce côté est de 5,9
Voili voilou
#9 - 24-02-2012 20:20:04
- MacArony
- Passionné de Prise2Tete
- Enigmes résolues : 49
- Messages : 52
- Lieu: Liège
Concous Griego 1&2.
Chien qui court dans la cour ne mérite aucun discours, mais lion qui accourt sans recours, au secours !
#10 - 25-02-2012 00:51:00
- Grizix
- Habitué de Prise2Tete
- Enigmes résolues : 30
- Messages : 31
Concours Griego &2.
2 - J'appelle (8^4) l'angle entre le segment de 8cm et celui de 4cm et (4^6) entre le segment de 4cm et celui de 6cm, etc ...
D'après Al-Kashi :
cos(8^4) = (8²+4²-5²)/(2*4*8)
cos(4^6) = (4²+6²-3²)/(2*4*6)
x² = 8²+6²-2*8*6*cos(8^6)
Formule de trigo :
cos(8^6) = cos(8^4+4^6) = cos(8^4)cos(4^6) - sin(8^4)sin(4^6)
Pour les sinus, on aura donc des sin(acos(.../...)).
En calculant tout ça, et en prenant la valeur positive, j'obtiens :
x = 69.2mm
Pour la question 1, je ne comprend pas ce qui mesure 5, ce que font les barres pour dire que les segments sont égaux, par rapport à quel milieu, le dessin est-il bien proportionné ? Parce que si non, l'énoncé n'est pas vraiment suffisant pour comprendre.
#11 - 25-02-2012 03:38:16
- emerald000
- Amateur de Prise2Tete
- Enigmes résolues : 44
- Messages : 7
#12 - 25-02-2012 08:56:31
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
Concours Griego 1&.
Salut !
Bon, pour la première ce n'est pas bien compliqué : Il suffit de tracer le rayon du cercle qui passe par le point de tangence du haut. On obtient alors une situation de Thalès (puisque ce rayon est perpendiculaire à la dite tangente, et donc parallèle au côté de longueur x) qui donne 7.5/10=2.5/x; d'où x=10/3
Pour le second, je ne trouve de manière simple de traiter le problème... je sors donc l'artillerie lourde 
Pour commencer, j'appelle A le point en bas à gauche, B celui en bas à droite, C celui du haut et I le point qui reste à l'intérieur du grand triangle.
Méthode :
Calculer les aires des triangles ABI et IBC à l'aide de la formule du héron.
En utilisant la loi des sinus pour calculer les mêmes aires, on obtient les angles ABI et IBC, on peut donc trouver l'angle ABC par somme des deux précédents.
Je trace la hauteur du triangle ABC dont la base est le côté de longueur 8, et j'appelle le pied de cette hauteur H.
Grace à la trigo dans BCH et l'angle HBC, je trouve les longueurs CH et BH.
J'en déduis AH = 8 - BH
Enfin, j'utilise Pythagore dans le triangle rectangle AHC et j'obtiens AC.
Mes résultats intermédiaires me donnent (arrondis à 3 chiffres significatifs) :
Aire ABI=8.18
Aire IBC=5.33
Angle ABC = 0.997 (en radians)
CH=5.04
AH=4.74
Finalement, x=6.92159741728...
Edit : je viens de voir qu'on demande au 10eme de milimètre, donc : x=6.92 cm
#13 - 25-02-2012 10:13:40
- Promath-
- Elite de Prise2Tete
- Enigmes résolues : 18
- Messages : 1416
- Lieu: Au fond de l'univers
concourq griego 1&2.
Je ne dis rien sur vos résulats personnels pour l'instant, mais c'est très bien en moyenne!
Un promath- actif dans un forum actif
#14 - 25-02-2012 17:25:09
- L00ping007
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 2010
- Lieu: Paris
Concuors Griego 1&2.
Question 1
Avec un peu de Thales et de Pythagore, en remarquant qu'un carré est formé au
niveau du cercle, on a :
[TeX]\frac{2,5}x = \frac{\sqrt{50}}{\sqrt{50}+2,5}[/TeX]
Ce qui donne [latex]x\approx3,38cm[/latex]
Question 2
J'utilise la formule de Héron pour calculer les aires des 4 triangles, avec x la longueur inconnue.
Ensuite je m'aide de Wolfram Alpha pour résoudre une équation en [latex]x^2[/latex] de degré 2 :
[TeX]x \approx 6,921597...[/TeX]
#15 - 25-02-2012 19:39:17
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3222
- Lieu: Luxembourg
Concours Grego 1&2.
Bonjour,
Partie 1
Des triangles sont semblables, d'où:
x / (a + 2,5) = 2,5 / a, avec a = V(7,5² - 2,5²)
On trouve finalement:
a = 5V2, et x = 2,5 + 0,625V2
Soit a = 3,4 env.
Partie 2
Les relations sans un triangle quelconque aident:
x = V{5² + 3² - 2.5.3.cos [2.pi - acos(-23/40) - acos(-11/24)]}
Soit x = 6,92 cm env.
Bonne soirée.
#16 - 25-02-2012 21:34:01
- looozer
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 697
- Lieu: Belgique
Concourrs Griego 1&2.
1.
- Le rayon passant par le point de tangence est perpendiculaire à la tangente.
- En traçant celui qui est parallèle au segment inconnu on dessine donc un triangle rectangle semblable au grand.
- On calcule avec Pythagore la longueur de son 3ème côté : [latex]5\sqrt2[/latex]
- On multiplie la longueur du rayon par le rapport de similitude : [latex]2.5*\frac{(2.5+5\sqrt2)}{5\sqrt2}[/latex] soit environ 3.4
2.
- En utilisant la loi des cosinus dans les 2 triangles connus, on calcule les deux angles au centre : 117,2796127 et 125,0996322
- Pour compléter l'angle plein il faut encore 117,6207551
- Une nouvelle utilisation de la formule du début dans le 3ème triangle donne le côté manquant : environ 6.92
Merci pour les problèmes 
#17 - 25-02-2012 22:22:54
- FRiZMOUT
- Verbicruciste binairien
- Enigmes résolues : 49
- Messages : 2218
concours griegp 1&2.
1.
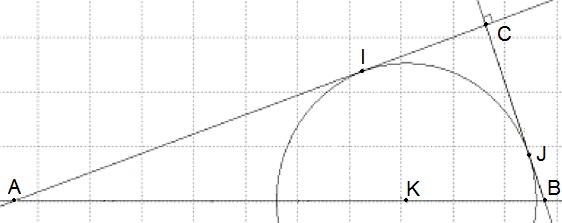
Par hypothèse, on a [latex]IK = KJ = 2.50[/latex] et [latex]\widehat{KIC} = \widehat{CJK} = \widehat{ICJ} = 90°[/latex].
[TeX]ICJK[/latex] est donc un carré et [latex]IC = CJ = 2.50[/latex] et [latex]\widehat{IKJ} = 90°[/latex].
Dans le triangle[latex] AIK[/latex] rectangle en [latex]I[/latex], on peut appliquer le théorème de Pythagore :
[latex]AK^{2}=AI²+IK²[/TeX]
C'est-à-dire :
[TeX]AI² = AK²-IK² = 7.5²-2.5² = 50[/TeX]
Donc [latex]AI = 5\sqrt{2}[/latex]
[TeX](KJ)[/latex] étant parallèle à [latex](AC)[/latex], on peut appliquer le théorème de Thalès :
[latex]\frac{KJ}{AC} = \frac{JB}{CB}[/TeX][TeX]KJ \times CB=AC \times JB[/TeX][TeX]KJ\times(CJ+JB)=(AI+IC)\times JB[/TeX][TeX]2.50 \times (2.50+JB)=(5\sqrt{2}+2.5)\times JB[/TeX][TeX]2.50²+2.50\times JB=5\sqrt{2}\times JB+2.5\times JB[/TeX][TeX]JB = \frac{2.50²}{5\sqrt{2}}[/TeX][TeX]CB = CJ+JB = 2.50+\frac{2.50²}{5\sqrt{2}} = 3.38388...[/TeX]
Le segment [CB] a une longueur de 3,4.
2.
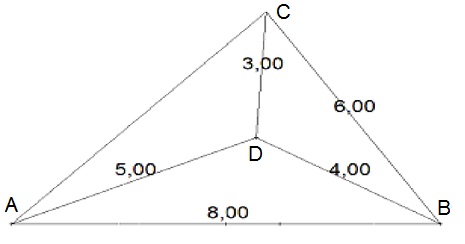
Dans le triangle [latex]ADB[/latex], on peut appliquer le théorème d'Al-Kashi :
[TeX]AB² = AD²+DB²-2 \times AD \times DB \times \cos{\widehat{ADB}}[/TeX]
Donc, [latex]\widehat{ADB} = \arccos(\frac{AD²+DB²-AB²}{2\times AD \times DB}) = \arccos(\frac{5²+4²-8²}{2\times 5\times 4}) [/latex]
[TeX]\widehat{ADB} = \arccos(-\frac{23}{40})[/latex] radians.
De la même façon dans le triangle [latex]CDB[/latex] :
[latex]CB² = CD²+DB²-2\times CD\times DB\times \cos{\widehat{CDB}}[/TeX]
Donc, [latex]\widehat{CDB} = \arccos(\frac{CD²+DB²-CB²}{2\times CD\times DB}) = \arccos(\frac{3²+4²-6²}{2\times 3 \times 4})[/latex]
[TeX]\widehat{CDB} = \arccos(-\frac{11}{24})[/latex] radians.
Pour finir, dans le triangle [latex]CDA[/latex] :
[latex]AC² = CD²+AD²-2\times CD \times AD \times \cos{\widehat{CDA}}[/TeX][TeX]AC² = 3²+5²-2\times 3\times 5\times \cos(2\pi-\arccos(-\frac{23}{40})-\arccos(-\frac{11}{24}))[/TeX][TeX]AC = \sqrt{34-30 \times \cos(\arccos(-\frac{23}{40})+\arccos(-\frac{11}{24})}[/TeX][TeX]AC = 6.921597...[/TeX]
Le segment [AC] a une longueur de 69,2 mm.
#18 - 26-02-2012 09:57:43
- Promath-
- Elite de Prise2Tete
- Enigmes résolues : 18
- Messages : 1416
- Lieu: Au fond de l'univers
Cocours Griego 1&2.
Un promath- actif dans un forum actif
#19 - 26-02-2012 14:39:06
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3500
- Lieu: 94110
concours griegi 1&2.
1 - En supposant que la distance de 5 est prise entre les points d'intersection les plus à gauche entre la droite horizontale et d'une part l'autre droite et d'autre part le cercle, on doit obtenir 9.571
2 - Là, il n'y a pas d'ambiguïté : 6.922
J'utilise la formule cos a = (b² + c² - a²) / 2bc pour calculer les "angles au centre" des 2 triangles connus.
Puis a² = b² + c² - 2 bc cos a pour calculer le coté inconnu.
EDIT :
Aaarrrgghhh ! Pour le 1 j'ai donné la longueur du grand coté de l'angle droit  ! !
#20 - 26-02-2012 18:08:42
- Promath-
- Elite de Prise2Tete
- Enigmes résolues : 18
- Messages : 1416
- Lieu: Au fond de l'univers
Concours Griegoo 1&2.
Bravo à tous
Réponses en cours d'enregistrement, ne modifiez rien!!
Un promath- actif dans un forum actif
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum











