 |
#1 - 27-03-2012 18:50:42
- Nombrilist
- Expert de Prise2Tete
- Enigmes résolues : 10
- Messages : 568
Probabilités: des lots dans nu lot
Bonjour à tous,
Ceci n'est pas à proprement parler une énigme, mais plutôt un problème que je n'arrive pas à résoudre.
J'ai 204 poissons. Parmi ces poissons, je suppose que j'ai 102 mâles et 102 femelles, mais ce n'est pas visible extérieurement. Je divise mes 204 poissons en 12 lots de 17 poissons chacun (12*17 = 204). Quelle est la probabilité pour que dans tous les lots, il y ait au moins 4 mâles et 4 femelles ?
Pour un lot, je pense que la loi hypergéométrique s'applique. Mais pour 2 lots et plus, comme les lots ne sont pas indépendants les uns des autres, tout de suite, ça complique. Enfin je crois. Du coup, j'aurais bien besoin de l'avis des spécialistes. Qu'en pensez-vous ?
Un grand merci aux futurs participants.
#2 - 28-03-2012 10:50:26
- NickoGecko
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1821
Probabilités: des lots dans uun lot
Bonjour,
Je n'ai pas le raisonnement complet, mais je me lance ...
J'aime bien l'idée du remplacement des boules blanches et noires par des poissons, et de l'urne par un aquarium !
On va imaginer que les 12 lots de 17 poissons sont prélevés successivement de l'aquarium.
> Il y a 18 possibilités de répartition (mâles; femelles), de (17;0) à (0;17)
> Jusqu'au 6ème prélèvement, elles sont équiprobables.
> Parmi les 18 possibilités, 10 répondent à la condition "au moins 4 mâles et 4 femelles" (de (4;13) à (13;4)
Donc, jusqu'au 6ème prélèvement, on a une probabilité de (10/18)^6 = 0,0294
que tous les lots satisfassent la condition initiale.
Au delà du 6ème prèlèvement, cela se corse !!!!
car si les 6 premiers sont (0;17) alors les 6 prochains seront forcément (17;0) !
.... j'en suis là ....
et si les poissons sont de cette espèce là :

Barbier ou Castagnole rouge ou barbier hirondelle
C'est une espèce hermaphrodite qui subit une inversion sexuelle au cours de sa vie; en effet d'abord femelle dans la première partie de son existence, l'individu devient ensuite mâle (Protogynie).
Les belles probabilités vont tomber à plat !
A bientôt !
Il aurait pu pleuvoir, con comme il est ! (Coluche)
#3 - 29-03-2012 20:35:34
- Nombrilist
- Expert de Prise2Tete
- Enigmes résolues : 10
- Messages : 568
Probabilitéés: des lots dans un lot
Bonjour NickoGecko,
Je ne vois pas pourquoi les 6 premiers tirages seraient équiprobables puisque par exemple, la probabilité que le second lot satisfasse à l'exigence dépend du tirage du premier lot.
Quand à l'espèce, je te rassure: elle est gonochorique.
#4 - 29-03-2012 23:44:53
- victosaurus
- Habitué de Prise2Tete
- Enigmes résolues : 5
- Messages : 40
Probabilités: des lots dasn un lot
Une idée qui peut peut être aider:
On commence par construire 12 lots en imposant 4 males puis 4 femelles:
(m m m m f f f f...) X 12
puis on "compte" de combien de manières on peut compléter les lots aléatoirement avec les 204-(8*12)=108 poissons restants. On divise alors ce nombre par le nombre total de lots que l'on peut construire sans contrainte.
#5 - 30-03-2012 00:14:56
- Nombrilist
- Expert de Prise2Tete
- Enigmes résolues : 10
- Messages : 568
probavilités: des lots dans un lot
C'est effectivement une approche intéressante. Mais comment dénombrer le nombre de combinaisons possibles avec ou même sans contrainte ? J'ai l'impression que l'ordre de tirage poisson par poisson est important. J'ai du mal à voir le problème autrement.
De fait, il s'agirait d'écrire un mot de 204 lettres contenant 102 "f" et 102 "m" et de couper ensuite ce mot en 12 tronçons de 17 lettres en dénombrant le nombre de cas où ces tronçons contiennent tous au moins 4 "m" et 4 "f".
Le nombre de façon d'arranger 102 "f" et 102 "m" dans un mot de 204 lettres est, me semble-t-il: 204! / 102!²
Parcontre, dénombrer le numérateur... ommagad !
#6 - 30-03-2012 01:24:20
- dhrm77
- L'exilé
- Enigmes résolues : 49
- Messages : 3004
- Lieu: Fanning Island-?-Lac Tele,Mali
rPobabilités: des lots dans un lot
Je n'ai pas calculé les probabilités, mais seulement fait des simulations.
(10 simulations successives, chaqu'une avec 100 millions d'essais (204 tirages par essai) )
Je trouve des résultats curieux:
La probabilité d'avoir au moins 4 mâles et 4 femelles est differente pour
chaque groupe:
1er groupe: 99.0624%
2eme groupe: 99.0628%
3eme groupe: 99.0599%
4eme groupe: 99.0649%
5eme groupe: 99.0613%
6eme groupe: 99.0613%
7eme groupe: 99.0592%
8eme groupe: 99.0669%
9eme groupe: 99.0597%
10eme groupe: 99.0612%
11eme groupe: 99.0673%
12eme groupe: 99.0567%
et enfin la probabilité que tous les groupes aient au moins 4 mâles et 4 femelles: 89.42794%
Les résultats de chaque test se ressemblent beaucoup:

Je me demande si c'est du a une caractéristique du générateur de nombres aléatoires que j'utilise.
Ce que je trouve assez interressant, c'est que si, au lieu d'avoir 12 groupes de 17 poissons, on a 12 groupes de 15 poissons, les résultats sont tres differents. Au lieu d'avoir le 12eme groupe avec la plus petite probabilité et le 11eme groupe avec la plus grande, c'est le 2eme groupe qui a la plus petite, et le 5eme groupe qui a la plus grande.
Great minds discuss ideas; Average minds discuss events; Small minds discuss people. -Eleanor Roosevelt
#7 - 30-03-2012 07:04:34
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
probabilités: dzs lots dans un lot
Ce sujet devient très intéressant !
Ton hypothèse de générateur aléatoire me semble la meilleure, car il n'y a que 0.01% donc 1 pour 10 000 de différence entre les valeurs extrêmes, et je n'y vois vraiment aucune raison logique! (Surtout en regardant les variations).
A moins qu'il ne s'agisse d'un arrondi car tu as quand même simulé 100 millions d'essais, soit plus de 20 milliards de tirages !
La démonstration reste à trouver...
#8 - 30-03-2012 08:56:12
- NickoGecko
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1821
Probabilités: des lots dans nu lot
Bonjour,
Nombrilist a écrit:Bonjour NickoGecko,
Je ne vois pas pourquoi les 6 premiers tirages seraient équiprobables puisque par exemple, la probabilité que le second lot satisfasse à l'exigence dépend du tirage du premier lot.
Effectivement, tu as sûrement raison.
victosaurus a écrit:Une idée qui peut peut être aider:
On commence par construire 12 lots en imposant 4 males puis 4 femelles:
(m m m m f f f f...) X 12
puis on "compte" de combien de manières on peut compléter les lots aléatoirement avec les 204-(8*12)=108 poissons restants. On divise alors ce nombre par le nombre total de lots que l'on peut construire sans contrainte.
Je suis aussi reparti sur une approche du même ordre.
On dénombre les compositions ou partitions de 204, ou plutôt de 102, en au plus 12 termes de valeur maximale égale à 17.
Un site internet propose ce calcul en ligne.
http://www.btinternet.com/~se16/js/partitions.htm
donc selon l'appli du site :
> Il y a 367483 partitions de 102 avec 12 termes de valeur maximale 17.
J'ai commencé à les énumérer :
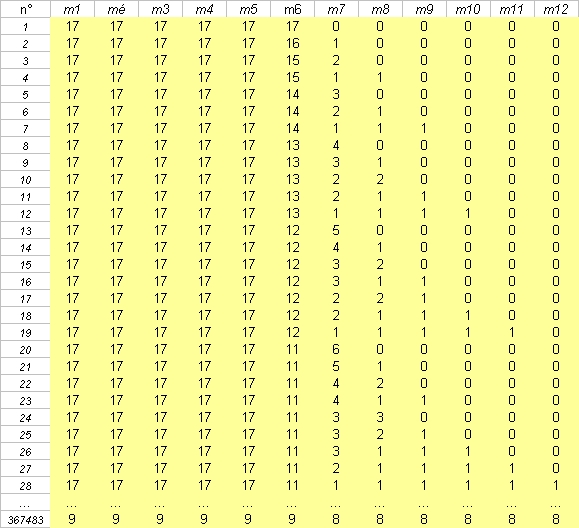
J'ai pris 102 pour partir du raisonnement avec l'un des deux genres, disons les mâles, d'ou l'indexation des termes de m1 à m12
Ce sont les partitions qui nous intéressent dans un premier temps, car ensuite pour les assimiler aux tirages, il y a beaucoup plus de possibilités que le calcul des compositions (voir les exemples du site)
Je pense que la suite du raisonnement consiste à :
Je l'imagine plus en programmation qu'en calcul pur, mais ne connaissant que VBA Excel je vais ramer !
1
Démultiplier chaque ligne parmi les 367483 selon le nombre de positions que ses termes distincts peuvent prendre. (suppose aussi de dénombrer combien il y a de termes distincts par ligne, en incluant "0")
Exemple, les les six "17" de la première ligne, et donc les six "0" peuvent s'écrire de 12x11 = 132 façons différentes si je ne me trompe pas.
(en fait pour k termes distincts, il y a A(12;k) arrangements)
2
Ecrire en correspondance de chaque ligne un 12-uplet {f1;f2;...;f12} des complémentaires à 17 de chaque {m1;m2;...;m12}
(f1+m1=17 ....)
3
Compter les lignes où tous les termes mi et fi sont >= 4 !
"yakafokon" !
A+
Il aurait pu pleuvoir, con comme il est ! (Coluche)
#9 - 30-03-2012 10:57:41
- Nombrilist
- Expert de Prise2Tete
- Enigmes résolues : 10
- Messages : 568
Probabilittés: des lots dans un lot
dhrm77, intuitivement, ton résultat de 9 chances sur 10 me paraît tout à fait possible. Et ça me rassure car j'ai 9 chances sur 10 de réussir mon expérience.
Numériquement, je propose la solution suivante:
On dénombre dans un mot de 204 lettres le nombre total de façon d'arranger 102 "m" et 102 "f". Soit:
204!/102!²
Puis la même chose, mais de façon à ce que chaque tronçon de 17 lettres contienne au moins 4 "m" et 4 "f".
Pour un groupe de 17 lettres, le nombre de façon d'arranger 4 "m", 4 "f" et 9 autres lettres, peu importe lesquelles:
17! / (4!*4!*9!).
Pour 12 tronçons, on élève à la puissance 12.
Pour les 108 lettres restantes, il reste à calculer le nombre d'arrangement de 54 "m" et 54 "f". Soit:
108! / 54!²
D'où, la probabilité finale: [(17!^12)*108!*102!²] / [204!*54!²*(4!*4!*9!)^12]
C'est ma proposition. Est-ce que vous pensez que c'est juste ? Quelqu'un a-t-un programme capable de calculer cela ? Ce sont des nombres trop élevés pour Excel.
#10 - 30-03-2012 14:26:02
- NickoGecko
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1821
ptobabilités: des lots dans un lot
Essaye tes calculs avec WolframAlpha ...
Un copier-coller de l'expression que tu proposes est "interprétée" et donne le résultat suivant :
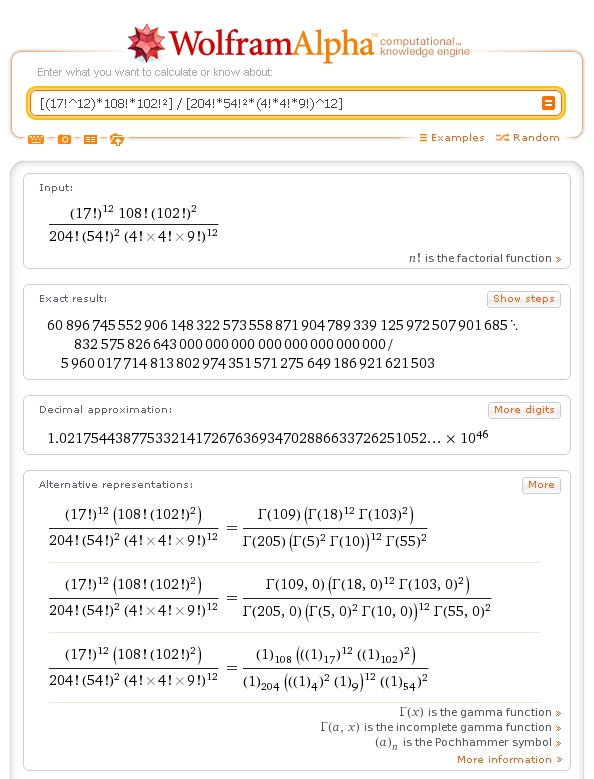
A voir ...
Il aurait pu pleuvoir, con comme il est ! (Coluche)
#11 - 30-03-2012 14:53:00
- Nombrilist
- Expert de Prise2Tete
- Enigmes résolues : 10
- Messages : 568
Probabilités: des ltos dans un lot
Merci, c'est le résultat exact. J'ai fait le calcul en simplifiant les termes et j'ai trouvé exactement le même résultat. Il y a une erreur de raisonnement au niveau de la façon d'arranger 4 "m", 4 "f" et 9 trous parmi les 17 emplacements d'un tronçon. Mais je n'arrive pas à comprendre pourquoi. Apparemment, les trous n'en sont pas.
#12 - 30-03-2012 15:12:42
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
probabulités: des lots dans un lot
Ma calculatrice me dit que ça fait 1,02175E46, lol !
Ça ne doit pas être ça...
J'ai une autre approche, et je pense que ça fonctionne puisque j'obtiens les même résultats que Drhm.
Je ne m'intéresse pour le moment qu'à un seul lot de 17 (le premier pour simplifier). Soit X la variable aléatoire qui compte le nombre de mâles.
La probabilité de n'avoir aucun mâle correspond à 102/204 pour le premier, puis 101/203 pour le second et ainsi de suite pour les 17 poissons :
p(X=0) = (102/204) x (101/203) x...x (86/188) = (102x101x...x86)/(204x203x...x188)
p(X=0) = (102!*187!)/(85!*204!)
De même, la probabilité de n'avoir qu'un mâle et qu'il arrive le dernier est :
p=(102/204)x(101/203)x...x(87/189) x (102/188)
Comme le mâle peut être à n'importe quelle position du groupe :
p(X=1) = (17;1)*p = 17*102!*187!/(204!*86!)*102 où (17;1) est le coefficient binomial
ensuite, p(X=2) = (17;2)*102!*187!/(204!*87!)*102*101
Et enfin : p(X=3) = (17;3)*102!*187!/(204!*88!)*102*101*100
En fait la formule générale est : p(X=k) = (17;k)*(187!/204!)*(102!/(102-k)!)*(102!/(85+k)!)
Bref, on obtient p(X<4)=p(X=0)+p(X=1)+p(X=2)+p(X=3)=0.004695675 environ
soit 0.4695675%
Par symétrie, on peut dire qu'il y a autant de chance d'avoir 1 2 ou 3 femelles, et que donc la probabilité d'avoir au moins 4 mâle et 4 femelles vaut :
p = 1 - 2*0.004695675 = 0.99060865 = 99.06%
Pour finir, et c'est surement là le noeud du problème : je pense qu'il y a autant de chance qu'il n'y ai pas assez de mâle ou de femelle dans chacun des lots, puisque chaque lot est indépendant.
C'est un peut comme dire combien il y a de chance que le 1 sorte au loto en 1er, ou en 2nd. La probabilité est la même ! Le fait que si il est déjà sorti en 1er ne change rien au problème, il y a toujours au départ 1 chance sur 49 qu'il sorte sur la boule 1 et une chance sur 49 qu'il sorte sur la boule 2 !
Conclusion : la probabilité qu'il y ait assez de mâle et de femelle dans chaque lot vaudra :
p=0.99060865^12=89.29% !
#13 - 30-03-2012 16:51:18
- Nombrilist
- Expert de Prise2Tete
- Enigmes résolues : 10
- Messages : 568
Pobabilités: des lots dans un lot
"Pour finir, et c'est surement là le noeud du problème : je pense qu'il y a autant de chance qu'il n'y ai pas assez de mâle ou de femelle dans chacun des lots, puisque chaque lot est indépendant."
D'après moi, les lots ne sont pas indépendants car une relation mathématique les lie entre eux. En effet, il y a des combinaisons que tu prends en compte mais qui sont impossible. Par exemple, il ne peut pas y avoir 12 lots de 17 mâles.
D'ailleurs, la modélisation de drhm77 montre bien que la probabilité décroît avec le groupe. Ceci dit, apparemment, il semble que l'on puisse négliger la dépendance entre les lots, vu la très faible différence entre ton résultat et celui de dhrm. Bravo, car du coup je pourrai appliquer ta formule pour les manips à venir.
Drhm, ton programme m'intéresse beaucoup. C'est open-source ? 
#14 - 30-03-2012 20:25:57
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
Probabilités: des lots dans un lo
D'ailleurs, la modélisation de drhm77 montre bien que la probabilité décroît avec le groupe.
Je n'ai pas vu la même chose : Perso j'ai remarqué que ça montait, puis descendait, puis montait, etc. et dans des proportions infimes de surcroît...
Ah, et j'oubliais : Où as-tu vu que je prenais en compte des combinaisons impossibles ?
#15 - 30-03-2012 21:08:06
- Nombrilist
- Expert de Prise2Tete
- Enigmes résolues : 10
- Messages : 568
Probabilités: es lots dans un lot
Dans ton raisonnement, à moins que j'ai mal suivi, tu inclues par exemple la probabilité qu'il y ait zéro mâle (ou femelle) dans tous les groupes en même temps. Ce qui est impossible.
#16 - 30-03-2012 23:20:55
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
Probabilits: des lots dans un lot
Non, je ne pense pas.
Si je dis qu'il y a une chance sur 49 que la première boule du loto sorte le 1, et qu'il y a aussi une chance sur 49 que la deuxième sorte le 1, c'est une question d'arrangement d'un échantillon de 5 boules parmi 49. Ça ne veut pourtant pas dire qu'il est donc possible qu'elle sorte sur la boule une ET sur la boule 2 !
(Une fois le tirage terminé, j'ai une chance sur 49 que la boule 1 soit sortie sur la boule 1, autant sur la boule 2, et de même jusque la boule 5, et j'ai enfin 44 chances sur 49 qu'elle ne soit pas sortie)
En fait, je ne m'occupe que du calcul du premier lot car c'est le plus facile à calculer. Dans ce groupe précis, je calcul juste les chances d'obtenir 0, 1, 2 ou 3 mâles. Ce qui est possible. Je ne m'intéresse pas aux autres lots, de même que je ne m'intéresse pas aux autres boules du loto pour calculer la probabilité que le 1 sorte la première ou la deuxième boule.
Ensuite, une fois le premier lot analysé, je pense que tous les groupes ont la même probabilité d'avoir au moins 4 mâles et 4 femelles, puisqu'il s'agit d'un arrangement de la population (toujours la même référence que pour le loto).
L'ordre a donc une importance pour le calcul dans un lot, mais plus ensuite pour chaque lot, puisque chacun est un arrangement de 17 parmi 204...
Je ne sais pas si je suis très clair, je suis désolé... 
#17 - 30-03-2012 23:43:07
- Nombrilist
- Expert de Prise2Tete
- Enigmes résolues : 10
- Messages : 568
Probabilités: des lots dan un lot
Je comprends à peu près ce que tu dis, mais je ne pense pas que l'on puisse comparer au loto.
Pour le lot X1, tu dis que P(X1>3) = [1 - P(X1=0) - P(X1=1) - P(X1 =2)]
Et ainsi de suite jusqu'à X12. Pour un lot pris séparément, c'est exact.
Mais ensuite, tu considères les X1...X12 équivalents et indépendants et donc tu élèves la formule à la puissance 12. Tu es donc d'accord avec moi que ta formule contient bien le terme [P(X1=0)*P(X2=0)*...*P(X12=0)]. Ce terme devrait être absolument nul puisque c'est un évènement impossible. Mais dans ta formule, il ne l'est pas. Et je prends le cas le plus simple. Des évènements impossible, je pense qu'il y en a plein dans ta formule.
#18 - 31-03-2012 06:10:15
- dhrm77
- L'exilé
- Enigmes résolues : 49
- Messages : 3004
- Lieu: Fanning Island-?-Lac Tele,Mali
Probabilités: des lots dans un lto
J'ai refait les meme tests avec le meme programme mais sur un ordinateur different, et donc un generateur de nombres aleatoire different, et les resultats sont maintenant differents. Au lieu d'avoir des tests qui se ressemeblent beaucoup, les resultats varient beaucoup.
Mais maintenant, la moyenne de chaque groupe est de 99.0602%.
Puisque Nombrilist me demande le programme, le voici:
Great minds discuss ideas; Average minds discuss events; Small minds discuss people. -Eleanor Roosevelt
#19 - 31-03-2012 08:09:14
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
Probabilités: des lots dans unn lot
Bah, les probas me semblent toujours si compliquées 
Je comprends aussi ton point de vue maintenant, mais je ne pense pas que ma formule contienne P(X1>3) = [1 - P(X1=0) - P(X1=1) - P(X1 =2)], mais plutôt :
P(3<X1<14) = 1 - [P(X1=0) - P(X1=1) - P(X1 =2)] x 2 puisque j'ai précisé qu'on avait autant de chance de ne pas avoir 4 mâles que de ne pas avoir 4 femelles.
Il reste en revanche a regarder si ma formule contient ou non :
[P(X1=4)*P(X2=4)*...*P(X12=4)], ce qui est également impossible.
Et là je n'ai pour le moment pas d'argument clair à présenter...
En fait, il faut s'attacher à regarder si on doit regarder chaque lot comme élément indépendant puisque la répartition est aléatoire dans chaque lot ou si la création des lots suivants dépendent du premier.
#20 - 31-03-2012 08:27:19
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
Prrobabilités: des lots dans un lot
Bon, pour plus de lisibilité j'ai recommencé mon exemple plus simple une page plus loin.
#21 - 31-03-2012 14:05:18
- MthS-MlndN
- Hors d'u-Sage
- Enigmes résolues : 49
- Messages : 12,414E+3
- Lieu: Rouen
probabilités: drs lots dans un lot
Bon, j'ai essayé quelque chose, mais c'est à compléter.
Je répartis les 204 poissons dans 12 bocaux de 17 poissons. Pour ça, j'en place 17 dans le premier bocal (parmi 204 : C(204,17) possibilités), puis 17 parmi les 187 qui restent dans le second (C(187,17) possibilités), etc. En développant le produit de C(204,17)*C(187,17)*C(170,17)*...*C(34,17), je réalise que je peux simplifier pour garder au final (204!)/(17!)^12.
Une autre façon de l'expliquer :
- 204! est le nombre de tirages différents des 204 poissons, puisque je considère que je les tire l'un après l'autre et qu'ils y auront tous le droit
- (17!)^12 est le nombre de tirages différents qui donneront la même répartition finale, puisque je peux tirer 17 poissons d'un même bocal dans n'importe quel ordre et qu'il y a 12 bocaux
Quand j'en suis là, je considère toujours qu'il y a un "premier" bocal, un "deuxième", etc. Vu que l'ordre m'est indifférent, je divise le tout par 12!, c'est-à-dire le nombre d'ordres différents pour 12 bocaux au contenu identique.
Finalement, j'ai (204!)/[12!*(17!)^12] façons différentes de répartir 17 poissons dans 12 bocaux, soit 6,7515443725.10^(200).
Une formule plus générale, pour répartir n poissons dans k bocaux de j poissons (j*k=n), serait n!/[k!*(j!)^k]
NB : si on se limite à deux lots, on obtient n!/[2*(k!)^2], qui est rigoureusement exact puisque n!/(k!)^2 est C(n,k) et que le facteur 2 sert à dire que les séparations en deux lots sont identiques 2 à 2. Cela me donne encore un argument de plus semblant justifier l'exactitude de ce calcul.
Pour le nombre de répartitions qui respactent la condition "4 mâles et 4 femelles par bocal", j'ai tenté la méthode "on met 4 mâles et 4 femelles par bocal, puis on complète au hasard", mais en procédant de la sorte, on peut retomber sur des partages identiques...
Podcasts Modern Zeuhl : http://radio-r2r.fr/?p=298
#22 - 31-03-2012 17:26:12
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
Probabilités: des llots dans un lot
"Pour le nombre de répartitions qui respactent la condition "4 mâles et 4 femelles par bocal", j'ai tenté la méthode "on met 4 mâles et 4 femelles par bocal, puis on complète au hasard", mais en procédant de la sorte, on peut retomber sur des partages identiques..."
C'est bien aussi ce que j'ai tenté, mais je me suis aussi vite rendu compte que ça ne marchait pas...
#23 - 31-03-2012 19:06:10
- Nombrilist
- Expert de Prise2Tete
- Enigmes résolues : 10
- Messages : 568
Probabilités: des los dans un lot
Mathias, je ne comprends pas ta façon de dénombrer les arrangements de poissons. On dirait que tu considères que tous les poissons sont différents. D'après moi, ce n'est pas le cas car il n'y a que deux catégories de poissons: il y a 102 poissons mâles et 102 poissons femelles. Selon moi, les mâles sont identiques et les femelles aussi. Le nombre d'arrangement de 102 "m" et 102 "f" dans un mot de 204 lettres est de seulement 10^60 (à quelque chose près, et sauf erreur de ma part).
En fait: 204! / 102!²
Mais serait-il plus simple comme tu le suggères, de considérer les mâles et femelles comme tous différents ? Genre m1, m2...m102 et f1,f2...f102 ? A voir...
#24 - 01-04-2012 00:15:57
- victosaurus
- Habitué de Prise2Tete
- Enigmes résolues : 5
- Messages : 40
Probabilités: de lots dans un lot
Je me pose aussi la même question.
Perso je considèrerais les poissons comme indifférenciables à l'oeil comme tu le fais.
Par contre la notion de "mot" ne me parait pas correcte car tu differencies les positions des poissons. Je parlerais putôt de "sachets".
Par exemple avec 10 m et 7 f on peut faire un seul sachet mais beaucoup de mots.
Je me demande si l'on est pas en train de noyer le poisson dans l'eau? 
#25 - 01-04-2012 11:26:08
- NickoGecko
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1821
Probabilités: des lots daans un lot
Hello
Je reviens sur mes partitions et l'envie de résoudre par la programmation plutôt que par la théorie.
(cf le tableau excel en copie d'écran dans un de mes posts ci-dessus ...)
En effet, je me suis lancé dans les partitions, mais la théorie de celles-ci n'inclut pas "zéro" dans la décomposition !
Comme je veux dénombrer toutes les partitions de 102 en 12 termes de 0 à 17, je fais tourner 12 boucles for/next de 18 termes.
Soit 18^12 = 1E15 itérations.
(j'ai essayé d'introduire des tests pour reboucler + vite, mais je ne suis pas sûr que le temps du test optimise le temps des boucles inutiles)
Au bout de 10 minutes sur Excel / VBA j'ai trouvé environ 1E7 lignes.
Donc si je compte bien, j'en ai encore pour les 1920 prochaines années ...
... avant de faire tourner les mêmes 12 boucles de 4 à 13 pour dénombrer les cas souhaités par l'énoncé !
Pensez-vous qu'un algo moins "bourrin" puisse aller plus vite ?
et/ou dans un autre langage ? (je ne connais pas le C ....)
A bientôt,
Il aurait pu pleuvoir, con comme il est ! (Coluche)
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum










