 |
#26 - 01-04-2012 11:42:42
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3834
Probaiblités: des lots dans un lot
Pour une partition, j'ai, pour ce problème, 54 à partitionner en somme de 12 nb max de valeur max 9.
Explication: 102 M se partitionne en 12 lots dont 4 min dans chaque lot et 13 max (si >13, F sous représentée).
Si on ôte les 4 min: 102-12*4=54. et le max passe donc de 13 à 9.
#27 - 01-04-2012 12:47:28
- Nombrilist
- Expert de Prise2Tete
- Enigmes résolues : 10
- Messages : 568
Probabilités: des lotss dans un lot
Je suis en train de faire tourner un algo en turbo pascal avec 12 boucle "for" en série variant de 4 à 13 (ce qui correspond à au moins 4 mâles et 4 femelles par lot). A chaque lot, je peux ainsi associer une probabilité hypergéométrique dépendante des tirages des lots précédents. J'espère ainsi passer en revue toutes les possibilités et avoir la réponse dans 48 heures.
#28 - 01-04-2012 13:37:56
- NickoGecko
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1822
probabilités: des lots dans un lpt
@ nodgim
je suis d'accord, 12 boucles de 4 à 13 (17 moins 4) pour retenir celles dont la somme fait 102
est équivalent à 12 boucles de 0 à 9 et ne retenir que celles dont la somme fait 54.
(on "translate" tout de 4 vers le bas, et le total de 104-4*12 = 48
Je suis d'accord, mais pour moi cela fait le même nombre d'itérations
@ nombrilist
merci de te lancer dans l'algo,
cependant, je pense qu'il y a deux dénombrements à faire tourner pour trouver la probabilté, sauf si, mais je n'ai pas bien compris, tu introduis à nouveau un tirage de nombres aléatoire ...
1 : toutes les "partitions" de 102 dénombrant l'ensemble des possibilités (le dénominateur de la probabilité)
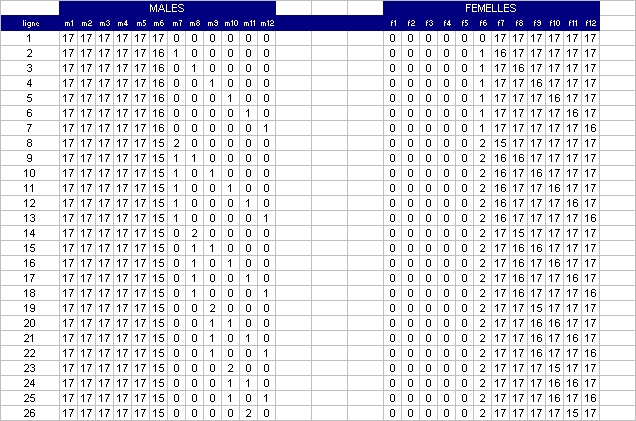
2 : les partitions de 102 avec des termes entre 4 et 13 (ou avec la translation de nodgim) = le numérateur de la probabilité
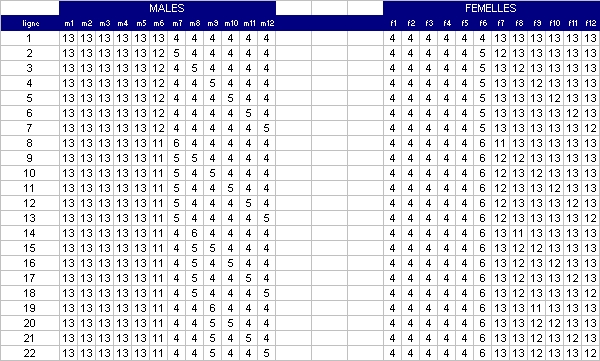
Le code pour le 1. :
Je vous autorise à dire que je programme comme un cochon !
- un algo de bourrin ! (je n'ose même pas dire "force-brute" !)
- des "goto" à toutes les sauces
- des "for / next" là où des do / until / loop (ou while) seraient plus élégants !
- et pas d'indentation pour améliorer la visibilité, ni de commentaires !
A+
Il aurait pu pleuvoir, con comme il est ! (Coluche)
#29 - 01-04-2012 14:25:08
- dhrm77
- L'exilé
- Enigmes résolues : 49
- Messages : 3004
- Lieu: Fanning Island-?-Lac Tele,Mali
probabilités: des lotd dans un lot
NickoGecko a écrit:(je ne connais pas le C ....)
C'est peut etre l'occasion de l'apprendre... Ca ne prend guere qu'une semaine ou 2.
Great minds discuss ideas; Average minds discuss events; Small minds discuss people. -Eleanor Roosevelt
#30 - 01-04-2012 14:33:24
- NickoGecko
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1822
Probabilités: de slots dans un lot
Tu as raison, et je ne demande qu'à apprendre (il n'est jamais trop tard !) mais étant un peu isolé question informatique, et n'en ayant pas vraiment besoin dans mon boulot, je n'ai jamais su par quel bout commencer et me suis contenté de bricoler des macros VBA ...
Bon j'ai trouvé ce site : http://www.siteduzero.com/tutoriel-3-14 … -en-c.html
pour me lancer !
Te tiendrai au courant de ma progression !
PS : à titre d'exemple, comment traduirais-tu en C les 12 boucles imbriquées (+/- les tests intermédiaires de sortie de boucle, si pertinents ?)
Un programme en C tourne-t'il plus vite, sur un même PC, qu'une macro VBA fusse-t'elle "élégante" ?
= penses-tu que les 12 boucles de [0 à 17] imbriquées puissent se terminer dans un temps "raisonnable" ? (quelques heures ....)
Bon Dimanche !
Il aurait pu pleuvoir, con comme il est ! (Coluche)
#31 - 01-04-2012 15:41:27
- Nombrilist
- Expert de Prise2Tete
- Enigmes résolues : 10
- Messages : 568
probabolités: des lots dans un lot
En gros, Nickogecko, j'ai fait un algo qui ressemble au tiens, sauf que je n'ai pas généré de tableur. Je fais bien 12 boucles qui varient de 4 à 13 (ce qui revient à varier de 0 à 9) et je ne prends en compte que les combinaisons de 12 variables dont la somme est égale à celle des mâles (ou des femelles, c'est pareil: 102). Puis je calcule à l'aide de la loi hypergéométrique la probabilité que la combinaison de 12 variables puisse effectivement avoir lieu. Et je somme au fur et à mesure.
Note: ça aurait surement été beaucoup plus rapide de dénombrer les probabilités des cas de 0 à 3 et de 14 à 17, comme proposé par Golgot je crois. Mais je n'y ai pensé qu'après coup.
#32 - 01-04-2012 18:26:59
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3834
probabilités: des kots dans un lot
A NickoGecko: bien sûr que ça donne le même nombre de possibilités, c'est juste que c'est un peu plus économe en écriture.
#33 - 02-04-2012 08:15:49
- MthS-MlndN
- Hors d'u-Sage
- Enigmes résolues : 49
- Messages : 12,414E+3
- Lieu: Rouen
probabilités: des lots dans un lor
Nombrilist a écrit:Mathias, je ne comprends pas ta façon de dénombrer les arrangements de poissons. On dirait que tu considères que tous les poissons sont différents.
C'est le cas. Je pensais que ça simplifierait le décompte des cas "favorables" à ta condition "4 mâles et 4 femelles au moins par bocal". Pas dit 
Podcasts Modern Zeuhl : http://radio-r2r.fr/?p=298
#34 - 02-04-2012 17:53:12
- Nombrilist
- Expert de Prise2Tete
- Enigmes résolues : 10
- Messages : 568
Probabilités: ddes lots dans un lot
Mon algorithme, qui a tourné pendant 36 heures, donne 0.894157384954208. C'est très proche du résultat de Golgot et de la modélisation de dhrm.
#35 - 02-04-2012 19:43:10
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
Probabilités: des lots dans unn lot
Bon, pour plus de lisibilité je recommence ici :
J'essaie avec 3 mâles et 3 femelles divisés en 3 lots de 2 poissons.
On a (6;3) = 20 combinaisons possibles.
1.MM MF FF
2.MM FM FF
3.MM FF MF
4.MM FF FM
5.MF MM FF
6.MF MF MF *
7.MF MF FM *
8.MF FM MF *
9.MF FM FM *
10.MF FF MM
11.FM MM FF
12.FM MF MF *
13.FM MF FM *
14.FM FM MF *
15.FM FM FM *
16.FM FF MM
17.FF MM MF
18.FF MM FM
19.FF MF MM
20.FF FM MM
Ici la proportion d'obtenir au moins un gars et une fille dans chaque lot est de 8/20 = 2/5.
Etude du premier lot :
Avec ma méthode de calcul, j'aurai :
p(X1=0)= (2;0) * 3/6 * 2/5 = 1/5 de ne pas avoir de mâle dans le premier lot.
Donc p(0<X1<2) = 1-2*1/5 = 3/5 soit 3 chances sur 5 d'obtenir un de chaque dans le premier lot, jusque là ça va !
Pour le 2ème lot : Il faut différencier les 3 cas : X1=0, X1=1 et X1=2
si X1=0 : alors on a 3 mâles et 1 femelle à se partager
p(X2=0) = 1/4 * 0/3 = 0
p(X2=1) = (2;1) * 1/4 * 3/3 = 1/2
p(X2=2) = 3/4 * 2/3 = 1/2
si X1=1 : alors on a 2 mâles et 2 femelles à se partager
p(X2=0) = 2/4 * 1/3 = 1/6
p(X2=1) = (2;1) * 2/4 * 2/3 = 2/3
p(X2=2) = 2/4 * 1/3 = 1/6
enfin si X1=2 : alors on a 1 mâle et 3 femelles à se partager
p(X2=0) = 3/4 * 2/3 = 1/2
p(X2=1) = (2;1) * 1/4 * 3/3 = 1/2
p(X2=2) = 1/4 * 0/3 = 0
On a donc finalement : p(X2=0) = p(X1=0)*p(X2=0 (si X1=0)) + p(X1=1)*p(X2=0 (si X1=1)) + p(X1=2)*p(X2=0 (si X1=2))
p(X2=0) = 1/5 * 0 + 3/5 * 1/6 + 1/5 * 1/2
p(X2=0) = 1/5
On en déduit par symétrie que p(X2=2) = 1/5
Donc p(0<X2<2) = 1 - 2*1/5 = 3/5
C'est bien le même résultat que pour le lot 1, ce qui me paraît logique.
En fait, si le lot de 204 poissons est divisé en 17 lots de 12. Il s'agit d'un arrangement de tous les poissons. Une fois les poissons répartis dans des petits sacs, je trouverai très étrange de dire : "pour avoir plus de chance d'avoir au moins 4 mâles et 4 femelles, je te conseille de prendre plutôt le sac qui a été fait en 13eme position, c'est plus sûr." Il s'agit d'un arrangement, donc à moins de connaître les poissons dans les sachets préparés les premiers, je ne vois pas pourquoi les probas changeraient d'un lot à l'autre.
Pour en arriver à la probabilité finale d'avoir au moins 1 mâle et une femelle dans chaque lot, je me suis trompé :
p = (3/5)^3 = 27/125 au lieu des 2/5 annoncés à la suite de l'arbre du départ... c'est bien sûr faux, car il y a là interdépendance entre les tirages. Mais je ne vois pas comment corriger, ni pourquoi mes résultats trouvés précédemment concordent avec vos simulations.
#36 - 02-04-2012 19:52:53
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3834
probabilités: des lots dabs un lot
Moi j'ai au bout de 9 lots 0.89125...
au bout de 12 lots 0.8576...
Mais le calcul a été fait comme si il y avait une infinité de M et de F.
Donc, je ne suis pas non plus si loin que ça du résultat.
Ce dont je suis sûr: P>0.857...
#37 - 02-04-2012 20:32:51
- Nombrilist
- Expert de Prise2Tete
- Enigmes résolues : 10
- Messages : 568
Probabilités: des lost dans un lot
nodgim, tu as appliqué 12 fois la loi binomiale B(17,0.5) je suppose ?
Golgot: on peut peut-être en conclure que l'interdépendance est faible ? D'ailleurs, l'application de la loi binomiale (qui considère que le lot dans lequel on pioche est infini) semble donner un résultat assez proche. Même pas 4 centièmes de différence.
Pour être plus clair sur mon algorithme, je prends tous les arrangements sur [4;13]12 tels que la somme des 12 fasse 102 (le nombre de mâles de ou de femelles total).
A chaque lot (tiré un par un), j'assigne dans l'ordre le nombre de mâle correspondant issu de [4;13]12. Puis j'associe à chaque lot tiré un par un la probabilité d'avoir tiré ledit nombre de mâles, connaissant le résultat du tirage pour le(s) lot(s) précédent(s). Cela donne 11 fois l'application d'une loi hypergéométrique à paramètres variables par tirage de 12-uplet.
J'estime que l'algo a passé en revue environ 43 milliards de combinaisons pour lesquelles la somme des 12-uplets fait 102.
#38 - 02-04-2012 23:49:55
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
Prrobabilités: des lots dans un lot
Bon, à force d'en parler, je suis allé voir ce qu'est une loi hypergéométrique... J'apprends ça (qui m'a l'air très intéressant) et je poursuis mes investigations 
#39 - 03-04-2012 02:00:09
- dhrm77
- L'exilé
- Enigmes résolues : 49
- Messages : 3004
- Lieu: Fanning Island-?-Lac Tele,Mali
rPobabilités: des lots dans un lot
NickoGecko a écrit:Tu as raison, et je ne demande qu'à apprendre
Je conseille la reference en la matiere: "the C programming language" de Kernighan and Ritchie (le fameux K&R), ou sa traduction francaise: "Le langage C", qui est une bonne traduction.
Great minds discuss ideas; Average minds discuss events; Small minds discuss people. -Eleanor Roosevelt
#40 - 03-04-2012 04:41:00
- NickoGecko
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1822
Probabiliéts: des lots dans un lot
Il aurait pu pleuvoir, con comme il est ! (Coluche)
#41 - 03-04-2012 22:59:35
- victosaurus
- Habitué de Prise2Tete
- Enigmes résolues : 5
- Messages : 40
Probabilités: ddes lots dans un lot
Finalement, quelqu'un sait il répondre à la question plus simple: de combien de manières différentes peut on obtenir 12 sachets de 17 poissons?
Je propose: Multinomial[17,17,17,17,17,17,17,17,17,17,17,17]/12!
soit:6.75....10^200
#42 - 04-04-2012 00:04:50
- Nombrilist
- Expert de Prise2Tete
- Enigmes résolues : 10
- Messages : 568
Probabilités: des lots dnas un lot
En considérant combien de catégories d'objets indiscernables ? 2 (mâles et femelles) ? Ou plus ? Et en considérant que l'on pioche dans un lot de 204 poissons ou bien dans un lot plus grand ?
Dans le premier cas, le résultat est majoré par [n!/(n1!*n2!)], avec n nombre total de poisson, et n1, n2 nombres de mâles et de femelles.
Soit (204!/102!²) = 1.43x10^60.
#43 - 04-04-2012 09:03:55
- NickoGecko
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1822
Probbabilités: des lots dans un lot
Bonjour !
Encore moi !
J'ai avancé sur l'algo de dénombrement des possibilités totales :
C'est à dire : chercher tous les {m1,m2,....,m12} avec m1+m2+...m12 = 102 (m1,m2,m3 ....m12 étant le nombre de mâles par sachet, donc entre 0 et 17)
Au lieu de faire tourner 12 boucles de 17 à 0 pour balayer en "brute force" toutes les "partitions" (nuance : avec le zéro) de 102 en 12 termes;
> Je fais tourner la boucle m1 de 17 à 0, la boucle m2 de m1 à 0, la boucle m3 de m2 à 0 etc ...
Cela réduit considérablement les étapes, car chaque {m1,m2,....,m12} dont la somme vaut 102, a ses termes classés en ordre décroissant, et est unique.
> Il faut alors, pour redéployer vers toutes les possibilités de tirage, calculer le nombre "d'arrangements" (ou "d'anagrammes") de {m1,m2,....,m12}
Mais nous sommes dans le cas d'arrangements "avec répétition",
Il faut donc calculer l'occurrence de chaque nombre entre 0 et 17
(Le nombre de mi termes égaux à 0, à 1, à 2 jusqu'à 1 ....)
Le nombre de possibilités de chaque ligne est égal à 12! divisé par le produit des factorielles de l'occurrence de chaque nombre entre 0 et 17 ...
Spoiler : Arrangements avec répétition, exemples : 
Le nombre total de tirages possibles est le cumul des possibilités de chaque ligne ainsi calculé avec brio. 
> Pour dénombrer les tirages qui remplissent la condition, je referai tourner le même algo entre 4 et 13.
> Pour l'instant je laisse tourner (et encore en VBA, désolé ...  ) )
J'espère que le temps de calcul sera ramené à un intervalle convenable pour revenir poster la réponse.
Qu'en pensez-vous ...?
A bientôt,
Il aurait pu pleuvoir, con comme il est ! (Coluche)
#44 - 04-04-2012 13:43:48
- victosaurus
- Habitué de Prise2Tete
- Enigmes résolues : 5
- Messages : 40
Probabilités: des lots dans un ot
@ Nombrilist: Il me semble qu'il faut consider tous les poissons différents (numérotés de 1 à 204). L'obectif étant de "compter" combien d'ensembles différents de 12 lots de 17 poissons on peut faire avec 204 poissons différents.
en prenant l'exemple de 3 lots de 2 poissons choisis parmi 6
12 34 56
12 56 34
12 43 56
correpondent a un même tirage.
par contre
12 35 46 correspond à un tirage tirage diférent des 3 précédents.
#45 - 04-04-2012 22:04:27
- Nombrilist
- Expert de Prise2Tete
- Enigmes résolues : 10
- Messages : 568
Probabilités: de lots dans un lot
A NickoGecko: si je ne me trompe pas, tu as tout simplement retrouvé mon 204!/102!². Tu peux arrêter ton algo ^^.
#46 - 05-04-2012 03:56:08
- NickoGecko
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1822
probabilités: des lots danq un lot
Nombrilist a écrit:C'est effectivement une approche intéressante. Mais comment dénombrer le nombre de combinaisons possibles avec ou même sans contrainte ? J'ai l'impression que l'ordre de tirage poisson par poisson est important. J'ai du mal à voir le problème autrement.
De fait, il s'agirait d'écrire un mot de 204 lettres contenant 102 "f" et 102 "m" et de couper ensuite ce mot en 12 tronçons de 17 lettres en dénombrant le nombre de cas où ces tronçons contiennent tous au moins 4 "m" et 4 "f".
Le nombre de façon d'arranger 102 "f" et 102 "m" dans un mot de 204 lettres est, me semble-t-il: 204! / 102!²
Parcontre, dénombrer le numérateur... ommagad !
Nombrilist a écrit:A NickoGecko: si je ne me trompe pas, tu as tout simplement retrouvé mon 204!/102!². Tu peux arrêter ton algo ^^.
Pas exactement ....
L'algo pour le dénombrement "total" n'a pas mis longtemps (10 minutes) et me donne :
901723 12-uplets différents de {17,17,17,17,17,17,0,0,0,0,0,0} à {9,9,9,9,9,9,8,8,8,8,8,8}
("différents" parce que j'ai limité les boucles avec m1>=m2>=m3>= ......m12)
qui générent 25354198128492 arrangements. (2,54E13)
Ton résultat 204!/102!² = 1,43E60
L'exécution de l'algo pour les tirages vérifiant la condition "au moins 4 mâles et 4 femelles" est très rapide (<1 minute) et donne :
8150 12-uplets différents de {13,13,13,13,13,13,4,4,4,4,4,4} à {9,9,9,9,9,9,8,8,8,8,8,8}
qui générent 39581170420 arrangements.
> La probabilité recherchée serait donc de 0,00156112885997843
Il aurait pu pleuvoir, con comme il est ! (Coluche)
#47 - 05-04-2012 11:25:27
- Nombrilist
- Expert de Prise2Tete
- Enigmes résolues : 10
- Messages : 568
probabilirés: des lots dans un lot
Ah OK, excuse-moi. En fait tu détermines l'ensemble des combinaisons de 17 lots de m et f satisfaisant la condition 102. Ensuite, tu calcules le nombre d'arrangements possible au sein de chaque lot. Effectivement, c'est ingénieux.
C'est très intéressant et je vais me pencher là-dessus. Mais le résultat de 1.5 pour 1000 me paraît bizarre. Le résultat de 0.9 est intuitivement bien plus plausible. En tout cas, je te remercie d'y passer tout ce temps. Je vais essayer de modéliser comme tu le fais pour voir.
Edit: encore une fois intuitivement, le problème doit venir du fait que tu dénombres et additionne des possibilités qui ne sont pas équiprobables. En effet, il me semble bien plus probable de faire {9;9;9;9;9;9;8;8;8;8;8;8} que {17;17;17;17;17;17;0;0;0;0;0;0).
#48 - 06-04-2012 07:09:17
- NickoGecko
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1822
probabilités: des lots dans un mot
Edit: encore une fois intuitivement, le problème doit venir du fait que tu dénombres et additionne des possibilités qui ne sont pas équiprobables. En effet, il me semble bien plus probable de faire {9;9;9;9;9;9;8;8;8;8;8;8} que {17;17;17;17;17;17;0;0;0;0;0;0).
Bonjour,
Je ne suis pas d'accord.
Mes tirages sont classés dans l'ordre, mais comme je calcule pour chaque tirage le nombre d'arrangements qui en découlent, j'aboutis bien à un dénombrement total.
Effectivement, deux de mes tirages "classés" n'ayant pas le même nombre d'arrangements ne sont pas équiprobables.
Pour les poissons :
Imagine 12 dés à 18 faces (de 0 à 17) que tu lances simultanément :
Il y a bien autant de probabilité de sortir six "9" et six "8"
{9;9;9;9;9;9;8;8;8;8;8;8} que six "7" et six "0" {17;17;17;17;17;17;0;0;0;0;0;0}
puisque dans ce cas, chaque tirage ayant deux termes différents, ils ont chacun 12!/(2!x2!) = 119 750 400 arrangements.
La question n'est pas la même, mais au loto, il y a autant de chances de sortir 1,2,3,4,5,6 que n'importe quelle autre combinaison !.
Qui joue cette combinaison saurait tout de suite si il a gagné !
Mais bon, pas à l'abri d'une erreur de raisonnement ou d'algo, je garde le fil si je me suis vraiment trompé qq part !
A bientôt,
Il aurait pu pleuvoir, con comme il est ! (Coluche)
#49 - 06-04-2012 08:50:13
- Nombrilist
- Expert de Prise2Tete
- Enigmes résolues : 10
- Messages : 568
Probabilités: des lots das un lot
Oui, mais ton dé à 17 face est pipé. Par exemple, à la formation du premier lot, la probabilité de faire 8 ou 9 (environ 0.19 pour chaque) est bien plus élevée que de faire 17 (environ 3.7*10^-6).
#50 - 06-04-2012 19:03:10
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3834
Probabiliéts: des lots dans un lot
Pour Nickogecko: quand tu as 7 M dans un lot, as tu pensé aussi à compter toutes les combis possibles de 7 parmi 17 ?
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum









