 |
#51 - 06-04-2012 21:42:32
- Nombrilist
- Expert de Prise2Tete
- Enigmes résolues : 10
- Messages : 568
Probabbilités: des lots dans un lot
Oui, en gros c'est ça ma remarque/question.
#52 - 07-04-2012 11:14:05
- NickoGecko
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1821
probabilutés: des lots dans un lot
Bonjour,
Désolé mais je ne comprends pas les dernières objections ...
Dans mon exemple avec les dés, j'ai omis le fait que leur total devait faire 102.
Mais je ne vois pas la question de non équi-probabilité.
Je propose qq chose : pourrait-on reprendre le même sujet avec moins de possibilités ? (nb de poissons ou nb de tirages inférieurs)
On y verrait peut être plus clair pour faire converger nos raisonnements ...
A bientôt,
Il aurait pu pleuvoir, con comme il est ! (Coluche)
#53 - 07-04-2012 13:13:50
- NickoGecko
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1821
probabilités: des lots sans un lot
Re !
J'ai gardé le principe de 17 poissons par tirage, mais avec 4 tirages seulement au lieu de 12.
Soit 68 poissons dans l'aquarium, 34 mâles et 34 femelles.
> Le nombre de possibilités est donné par 4 boucles tournant de 0 à 17, car il faut et il suffit de dénombrer un des deux genres, le nombre de poissons de l'autre genre étant égal au complémentaire à 17 de chaque terme du quadruplet {m1,m2,m3,m4}
On est d'accord ?
Dans ce cas, une simple macro Excel (Sorry dhrm !) écrit 3894 lignes
Si je fais tourner mon algo décrit précédemment (m1>=m2>=m3>=m4), je trouve 207 lignes qui se déclinent (anagrammes avec répétitions de lettres) en 3894 combinaisons ! (ouf !)
Voila pour le dénominateur.
> Idem entre 13 et 4 pour le numérateur
Faire tourner toutes les boucles me donne 670 lignes
L'algo me donne 43 lignes distinctes qui se démultiplient à .... 670 !
La probabilité alors d'avoir au moins 4 mâles ET 4 femelles dans chacun des 4 sachets est donc de 670/3894 soit 0.17
Etes-vous d'accord avec ceci ?
(je peux uploader les copies d'écran si nécessaire)
A bientôt,
Il aurait pu pleuvoir, con comme il est ! (Coluche)
#54 - 07-04-2012 18:11:41
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
Probablités: des lots dans un lot
Même sans rien vérifier,intuitivement, 0.17 me semble vraiment trop peu.
Tu as 34 M, 34 F, à répartir dans 4 bacs, et le hasard ne donne que 0.17 chance d'avoir au moins 4 M et 4 F dans chaque bac ? ça ne me semble pas raisonnable du tout.
#55 - 07-04-2012 18:20:48
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
Proabbilités: des lots dans un lot
Une répartition possible des 34 M:(13,13,4,4)
Nombre de combis possible:
D'abord à l'intérieur d'un bac: C(17,13) ou C(17,4)
Nb de répartitions de (13,13,4,4)=C(4,2)
Nb de combis total: C(4.2)*C(17.13)*C(17.13)*C(17.4)*C(17.4).
Il te reste à faire ce travail pour toutes les répartitions possibles, les 670 que tu as calculés.
Nb total de distributions dans les 4 bacs: C(68,34).
#56 - 07-04-2012 19:39:28
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
probabilités: dzs lots dans un lot
Bonsoir à tous 
Je n'ai pas trop suivi les réponses au problème mais la version simplifiée me semble bien plus sympathique .
34 poissons mâles et 34 femelles à répartir dans 4 aquarium . On cherche la probabilité pour que chaque aquarium contienne au moins 4 mâles et 4 femelles .
Il y a un problème classique de partition d'entier : p(n,k) nombre de décompositions de l'entier n en somme de k entiers ( positifs ou nul et en ordre croissant ) .
p(n,k) est calculable par induction à partir de p(n,k)=0 si n<k , p(n,n) =p(n;1)=1 et p(n,k)=p(n-1,k-1)+p(n-k,k) .
On dispose simplement les mâles dans les aquarium , les femelles viennent combler les vides .
Pour coller au problème on note p'(34,4) le nombre de partitions de 34 en 4 termes inférieurs ou égaux à 17 alors :
p'(34,4)=p(34,4)-p(16,3)-p(15,3)-...-p(0,3) .
Pour les décompositions favorables , il suffit de déposer 4 mâles dans chaque aquarium et de compléter avec un p(18,4) acceptable soit p"(18,4).
p"(18,4)=p(18,4)-p(4,3)-p(3,3)-...-p(0,3) .
La probabilité est alors p'(34,4)/p"(18,4) .
Je ne suis pas outillé ni motivé pour calculer ça mais si ça peut aider 
Vasimolo
#57 - 07-04-2012 20:09:39
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
rPobabilités: des lots dans un lot
#58 - 07-04-2012 20:49:42
- Nombrilist
- Expert de Prise2Tete
- Enigmes résolues : 10
- Messages : 568
Probabilités: des lots dans un lo
Vasimolo, en suivant ton développement, après un algorithme en TP7 (que j'espère avoir bien formulé), je trouve:
p'(68,4)=-1292
p''(52,4)=-808
p = 0.625 et des brouettes.
Le p semble possible, mais je suis surpris d'avoir des p' et p'' négatifs. C'est normal ?
Mon algorithme de construction de ton tableau p à deux entrées:
for k:=1 to 4 do p[0,k]:=0;
for k:=2 to 4 do p[1,k]:=0;
for k:=3 to 4 do p[2,k]:=0;
p[3,4]:=0;
for n:=0 to 68 do p[n,n]:=1;
for n:=2 to 68 do p[n,1]:=1;
for n:=1 to 68 do for k:=0 to 4 do if n>k then p[n,k]:=p[n-1,k-1]+p[n-k,k];
Ensuite, calculs de p' et p'':
p':=p[68,4];
for n:=3 to 50 do p':=p'-p[n,3];
p'':=p[52,4];
for n:=3 to 40 do p''=p''-p[n,3];
#59 - 07-04-2012 23:09:11
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
probabilirés: des lots dans un lot
J'ai un peu mélangé mâles et femelles , j'ai essayé de corrigé mais ce n'est pas garanti 
Vasimolo
#60 - 08-04-2012 06:56:49
- NickoGecko
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1821
Probabilités des lots dans un lot
Bonjour à tous !
@ nodgim : si je comprends bien, tu vas au niveau de détail de la répartition des mâles et des femelles à l'intérieur d'un bac de 17 poissons.
C'est à dire que, par exemple 12 mâles + 5 femelles peuvent être répartis dans 17 cases selon :
Mais je ne vois pas pourquoi cela aurait une incidence quelconque dans le résultat final.
Nous sommes au niveau "macro" (ni maquerau, ni macro-instruction" ). ).
J'imagine le tirage avec un sachet ou entonnoir qui prendrait exactement 17 poissons d'un coup dans le grand aquarium ...
@ Vasimolo : merci pour ta contribution !
Je pense que nos principes de résolution par "partition" se rejoignent, à un détail près : les partitions d'entiers et leur obtention par récursivité que tu décris sont pour n et k strictement positifs.
Or dans le problème posé, il est tout à fait possible d'avoir une répartition avec des termes nuls = aucun poisson d'un genre dans un bac !
Je vous livre mon tableau excel en pdf.
Un peu rébarbatif peut être, mais TOUTES les possibilités de "partitions" y sont et on y voit que le nombre de lignes ou tous les termes ne sont pas >=4 est important (3224) ce qui explique la faible probabilité à l'encontre de toute "intuition" ....
A bientôt pour la suite du "débat" !!! Bon Dimanche de Pâques ! 
Il aurait pu pleuvoir, con comme il est ! (Coluche)
#61 - 08-04-2012 10:03:17
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
Probabilités des lots dans un lot
A NG:
La combi (13,13,4,4) n'a pas la même valeur que la combi (17,17,0,0).
car C(17,13) et C(17,17) n'ont pas le même résultat. C'est, il me semble, ce qu'on a tenté déja de te dire.
#62 - 08-04-2012 11:18:28
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
probabilitéd: des lots dans un lot
Tu as raison NickoGecko , je n'avais pas fait attention au fait que les partitions considérées ne toléraient pas le 0 
On peut quand même garder l'idée en corrigeant les variables .
34 mâles à disposer dans 4 bocaux c'est p(38,4) à qui il faut retirer les partitions contenant plus de 18 mâles . Les solutions satisfaisantes sont p(22,4) moins les cas de dépassement .
J'essaierai de regarder en détail quand j'aurai un peu de calme à la maison 
Vasimolo
#63 - 10-04-2012 11:56:41
- NickoGecko
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1821
probabikités: des lots dans un lot
Re !
OK ! OK ! ... Je suis reparti tout au début avec une succession de tirages aléatoires du genre de chaque poisson "numéroté" de 1 à 204
La probabilité de prélever un mâle ou une femelle dépend effectivement des tirages précédents
Pour faire ce tableau, je determine aléatoirement le genre des premiers poissons, jusqu'à ce que l'effectif des mâles ou des femelles soit atteint auquel cas il n'y a plus de tirage au sort mais juste à complèter avec le genre restant .
(c'est ce qu'avait fait dhrm au début, en fait ...)
Les sous-totaux mâles / femelles sont calculés tous les 17 poissons = séparation des bacs.
(convention : 0 = femelle, 1 = mâle)
Ce qui m'a permis (qui a dit "enfin" ! ) de voir que l'on se rapprochait d'une distribution normale et pourquoi je ne pouvais effectivement pas prétendre à l'équiprobabilité de mes "partitions" .... ) de voir que l'on se rapprochait d'une distribution normale et pourquoi je ne pouvais effectivement pas prétendre à l'équiprobabilité de mes "partitions" ....
Je retrouve alors des probabilités entre 0,8 et 0,9 qui recoupent des valeurs déjà citées dans ce post. (en lançant des séries plus longues sans écriture dans le tableur)
tableau zoomable (complet) :

tableau zoomable (extrait) :
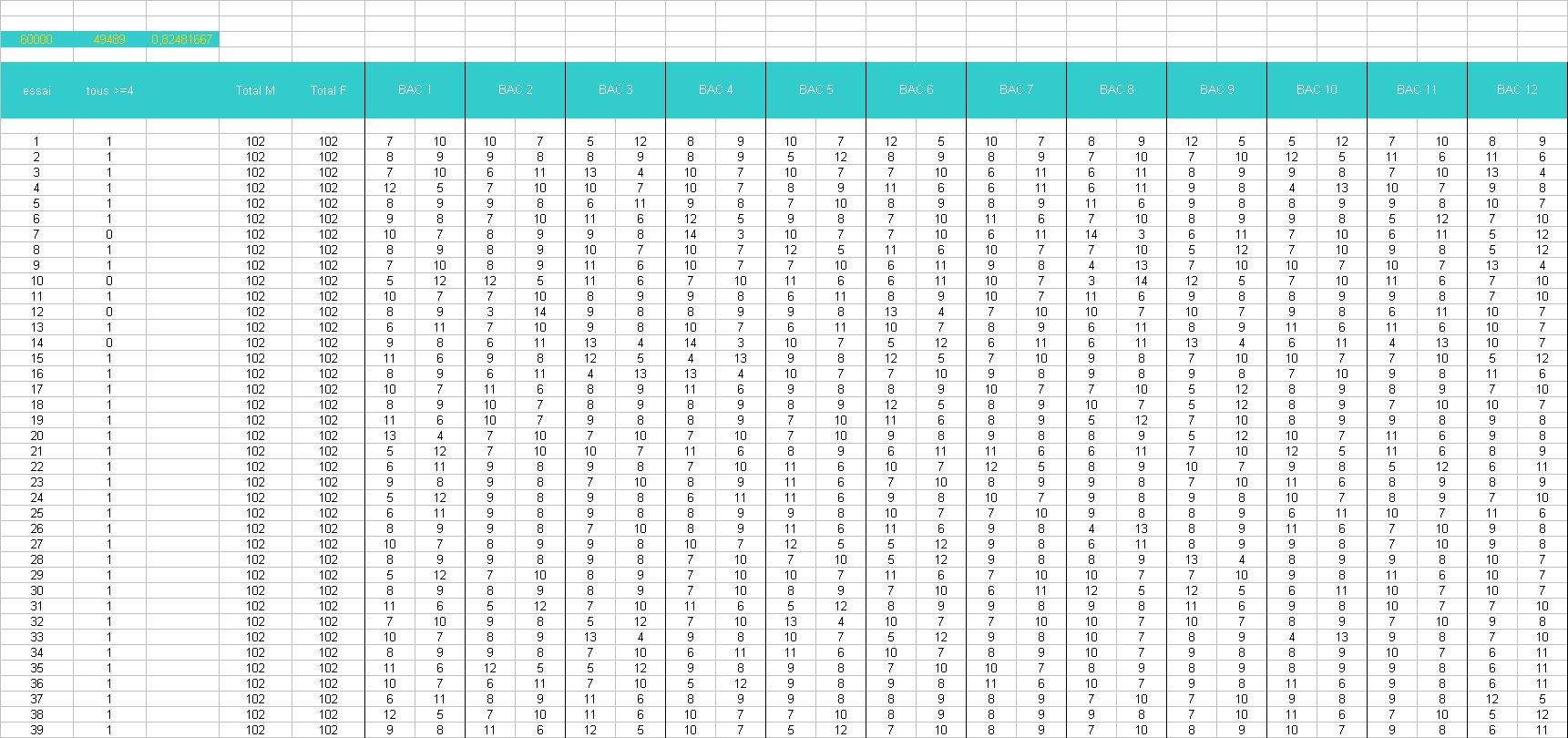
Ayant "débloqué" mon "point dur", je vais pouvoir à nouveau avancer dans le raisonnement et aussi mieux comprendre vos posts précédents ...
Je n'abandonne pas ma piste des "partitions", où chaque ligne que j'avais trouvée devra effectivement être affectée d'un coefficient (occurrence ?)
A+
Il aurait pu pleuvoir, con comme il est ! (Coluche)
#64 - 10-04-2012 21:24:54
- Nombrilist
- Expert de Prise2Tete
- Enigmes résolues : 10
- Messages : 568
Probabilité: des lots dans un lot
A chaque ligne au sein de chaque aquarium, tu devras appliquer la loi hypergéométrique.
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum








