 |
#1 - 26-08-2012 19:59:46
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
#2 - 27-08-2012 19:26:55
- Christian91
- Passionné de Prise2Tete
- Enigmes résolues : 0
- Messages : 89
- Lieu: 91
Echesc 13
euh ça me parait un peu simple ...
N'ai-je pas compris la question ?
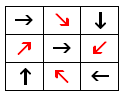
Le robot sur une des flèches rouges.
#3 - 27-08-2012 21:12:44
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Echec s13
Un exemple proposé par Christian :

Il y a une erreur sur la deuxième ligne et sur la deuxième colonne . Entre la deuxième et la troisième flèche l'angle est de 135° ( on parle d'angles entre vecteurs ) .
J'espère que cet exemple montre bien ce qui est autorisé et ce qui ne l'est pas 
Vasimolo
#4 - 28-08-2012 08:13:28
- halloduda
- Professionnel de Prise2Tete
- Enigmes résolues : 24
- Messages : 495
- Lieu: Ardèche
evhecs 13
Je ne crois pas.
Si on pouvait, il existerait un ensemble de vecteurs formant un circuit fermé minimal à l'intérieur duquel je pense qu'il y aurait nécessairement un angle > 90°...
#5 - 28-08-2012 12:34:48
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Ececs 13
@halloduda : Spoiler : [Afficher le message] D'accord pour le circuit , le reste c'est de la supputation 
Vasimolo
#6 - 28-08-2012 19:03:34
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
Echecs 3
Pour que le robot ne sorte pas, il doit faire un circuit fermé (on suppose un échiquier fini).
Un parcours fermé à une angulation globale de 360°.
Un parcours fermé de 4 cases ne convient pas (360°/4=90°)
Un parcours fermé en huit est impossible. il est en boucle unique, car il est impossible de réaliser des croisements de parcours. Le flêchage des cases intérieures est donc enfermé dans la boucle.
Soit on réalise un flêchage des cases intérieures en vortex vers l'extérieur ou l'intérieur, soit on réalise un flêchage en boucles concentriques. Dans tous les cas, on arrivera à une incompatibilité au centre.
#7 - 28-08-2012 19:29:47
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
echevs 13
Je ne vois pas pourquoi un robot ne pourrait pas sortir d'une boucle ou au moins en rejoindre la frontière !!!
Vasimolo
#8 - 29-08-2012 11:58:44
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Ehcecs 13
Juste un petit message pour dire que je ne donne pas d'indice vu la lourdeur de ma solution 
J'espère une idée originale et expéditive 
Vasimolo
#9 - 29-08-2012 14:34:26
- Klimrod
- Elite de Prise2Tete
- Enigmes résolues : 40
- Messages : 4050
- Lieu: hébesphénorotonde triangulaire
EEchecs 13
Bonjour,
Si le robot ne tombe pas, c'est qu'il effectue une boucle.
En effet, si N est le nombre de cases, alors au bout de N+1 mouvements, soit le robot est tombé, soit il est repassé par une case et donc il effectue un mouvement en boucle.
Puisque le robot effectue une boucle, on peut "évider" par l'esprit toutes les cases par lesquelles il ne passe pas et chercher ainsi le centre de gravité de la boucle.
Il y a alors quatre cas qui se présentent :
a) le centre de gravité de la boucle est sur une case du damier. Alors cette case ne peut pas avoir de flèche.
En effet, si elle en a une, elle n'est plus le centre de gravité.
b) le centre de gravité est sur une arête verticale entre deux cases. Alors chaque case de part et d'autre de l'arête doit avoir une flêche opposée horizontalement, ce qui n'est pas possible d'après l'énoncé.
c) le centre de gravité est sur une arête horizontale entre deux cases. Alors chaque case de part et d'autre de l'arête doit avoir une flêche opposée verticalement, ce qui n'est pas possible d'après l'énoncé.
d) le centre de gravité se trouve sur un angle entre quatre cases. Alors les quatre cases autour de cet angle doivent contenir des flèches telles que leur somme soit nulle, ce qui là encore n'est pas possible d'après l'énoncé.
Donc ma réponse est : non, ce n'est pas possible de trouver un tel tracé.
Klim.
PS. Tu vas dire que ce n'est pas très rigoureux, mais je suis certain que l'idée est là...
J'ai tant besoin de temps pour buller qu'il n'en reste plus assez pour bosser. Qui vit sans folie n'est pas si sage qu'il croit.
#10 - 29-08-2012 18:27:04
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
Eches 13
Si le robot ne s'enferme pas dans une boucle, tout en restant à l'intérieur de l'échiquier, il y a quelque chose qui m'échappe dans l'énoncé. Pour ce que j'ai compris, une flêche indique une seule case voisine, que le robot est tenu de suivre. Dès qu'il arrive dans la case voisine, il obéit alors à cette nouvelle flêche. Est ce autre chose ?
#11 - 29-08-2012 18:55:32
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
#12 - 29-08-2012 19:43:34
- franck9525
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1935
- Lieu: 86310
Echeecs 13
Le problème est de remplir le centre de la boucle.
Une boucle, arbitrairement orientée comme les aiguilles d'une montre, est caractérisée par deux changements d'orientation:
1/ Vers le haut sur le coté gauche (N) et vers le bas (S) sur la droite, ce qui impose une série "gauche-droite" comme étant N NE E SE S aux répétitions près.
2/ Du haut vers le bas, le série est toujours aux répétitions près.
E
SE
S
SO
O
Hors c'est deux séries ne s'assemblent pas comme il le faudrait, le "E" s’éloigne sur la diagonale montante et toute répétition éloigne d'avantage le "O" opposé.
Je note que l'on pourrait faire une analogie avec des valeurs octales.
Enfin il me semble que l'exercice n'est possible que pour des variations d'angles de 90 deg ce qui donnerait comme carré centrale la boucle elle-même.
N E
O S
The proof of the pudding is in the eating.
#13 - 30-08-2012 00:11:27
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
echevs 13
Lo po compris Franck 
Vasimolo
#14 - 30-08-2012 09:12:23
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3222
- Lieu: Luxembourg
Echecs 31
Bonjour,
Si j'ai bien compris, pour éviter une chute dans le vide, le robot devra effectuer une boucle fermée (plus ou moins grande) en périmétrie de l'échiquier carré. Le vecteur direction aura alors réalisé un tour complet. Si on prend maintenant des boucles de plus en plus petites à l'intérieur de celle du robot, comme il y aura de moins en moins de cases à parcourir, il est clair que le vecteur direction aura des angles de plus en plus grands à sauter et qu'à un moment, cet angle dépassera la valeur limite.
Voilà donc mon idée pour démontrer que c'est impossible, mais mon idée manque un peu (beaucoup) de rigueur mathématique.
Bonne journée.
#15 - 31-08-2012 00:11:03
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Ehcecs 13
Bonsoir à tous
Une approche possible qui m'avait presque convaincu . On suppose qu'il existe une boucle , alors en faisant tourner les flèches de ses cases d'un même multiple de 45° , on peut s'arranger pour que toutes les flèches pointent vers l'intérieur . On fait subir la même transformation à l'ensemble des flèches de l'échiquier et on est sûr que toutes les flèches à l'intérieur de la boucle pointeront vers une case de même nature . Il existe donc une nouvelle boucle ...
Mais ce n'est pas parce qu'on ne pointe pas vers un mur donné qu'on pointe forcément vers l'intérieur .
Vasimolo
#16 - 31-08-2012 03:15:07
Ecehcs 13
Ben, c'est quand même vraiment pas loin du théorème de la boule chevelue ton truc: si tu as une boucle, alors tu as une demi-boule avec un champ de vecteur continu le long, donc tu auras un épi à l'intérieur... Essaye en dimension impaire, ça change la vie!
#17 - 31-08-2012 12:32:57
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
#18 - 31-08-2012 18:30:15
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
Ehcecs 13
Je reviens sur mon raisonnement d'origine dont, il est vrai, la dernière phrase était trop vague.
Pour que le robot ne sorte pas, il doit faire un circuit fermé (on suppose un échiquier fini).
Un parcours fermé à une angulation globale de 360°.
Un parcours fermé de 4 cases ne convient pas (360°/4=90°)
Un parcours fermé en huit est impossible. il est en boucle unique, car il est impossible de réaliser des croisements de parcours. Le flêchage des cases intérieures est donc enfermé dans la boucle.
Ces assertions sont tout de même assez banales.
Soit donc une boucle, mettons qui tourne dans le sens horaire. Les cases voisines intérieures à la boucle sont soit:
-parallèles à la boucle (dans le sens horaire)
-décalées d'un 1/8 de tour vers la boucle, donc vers l'extérieur.
-décalées d'un 1/8 de tour vers l'intérieur. Dans ce cas là, cette flêche est origine d'un cheminement qui peut 1) rejoindre à un moment donné la boucle. Dans ce cas, il existe une boucle plus petite que la boucle originale et de même sens. C'est à dire qu'en partant de cette case, on reviendra sur une case voisine appartenant à la boucle originale. On ne pourra donc pas traverser cette boucle plus petite en partant d'une case intérieure. 2) soit le cheminement établira une boucle à l'intérieur de la boucle. Auquel cas on est alors confronté à la même configuration qu'avec la boucle originale.
Donc le problème peut se ramener à l'analyse des cases qui sont soit parallèles à la boucle soit orientées vers l'extérieur. On suppose qu'il n'y a que ces 2 possibilités, bien entendu mixées.
Une fois qu'on a placé les flêches dans les cases de cette boucle intérieure, on recommence avec une 3ème boucle à l'intérieur de la seconde. Le terme boucle ne désigne pas ici un cheminement, mais simplement un remplissage des cases intérieures immédiatement voisines de la boucle précédente. L'ensemble des cases est une boucle, même si ça ne correspond pas à la direction des flêches.
On continue ainsi couche après couche jusqu'à arriver à un nombre minimal de cases. Or on est toujours dans la configuration des flêches soit paralléles soit extérieures. Il est évident que dans la case finale on ne pourra pas orienter la flêche dans tous les sens à la fois. Et le problème va se poser bien avant la case finale, au minimum dans les 4 dernières cases à remplir, et encore si elles sont en carré.
Voilà à peu près mon raisonnement.
#19 - 01-09-2012 01:22:58
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
rchecs 13
A nouveau je lève le voile avant la fin du temps imparti . Il me semble que les problèmes un peu délicats dont le résultat est une explication à un phénomène ne gagnent rien à rester cachés longtemps .
Je m'en souviendrai pour la suite 
Vasimolo
PS : je prépare une solution complète que je posterai bientôt .
#20 - 01-09-2012 10:04:25
- Christian91
- Passionné de Prise2Tete
- Enigmes résolues : 0
- Messages : 89
- Lieu: 91
Ecchecs 13
nodgim a écrit:Je reviens sur mon raisonnement d'origine ...
Voilà à peu près mon raisonnement.
Belle explication. 
J'aime bien aussi : Klimrod a écrit:... chercher ainsi le centre de gravité de la boucle ...
bien que je ne vois pas comment la conclusion sur ce centre de gravité permet de conclure sur le problème posé ?
Je suis curieux de voir ce que sera la solution complète ...
#21 - 01-09-2012 11:35:48
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 5,996E+3
evhecs 13
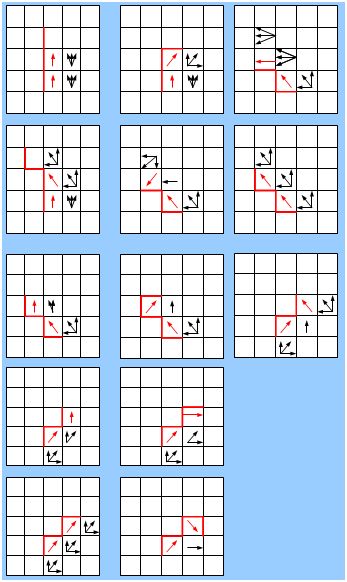
Je ne sais pas si c'est valable , mais je pense que s'il existe une boucle (on va dire qui tourne dans le sens des aiguilles d'une montre), on peut en tracer le tour en rouge. On voit alors qu'aucune des flèches qui se trouvent dans cette boucle ne permet d'en sortir.
Si une flèche permet de rejoindre cette boucle, c'est qu'on peut en trouver une plus petite en passant par cette case donc ou que cette case ne peut pas être atteinte.
Si aucune flèche intérieure ne permet de rejoindre la boucle, c'est qu'elles forment au moins une boucle plus petite.
Donc, s'il existe une boucle, il en existe une plus petite ou alors une boucle de 4 cases ce qui est impossible.
Aux symétries près, je pense que tous les cas sont là :
#22 - 01-09-2012 12:02:05
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
exhecs 13
"Si une flèche permet de rejoindre cette boucle, c'est qu'on peut en trouver une plus petite en passant par cette case donc ou que cette case ne peut pas être atteinte."
Phrase un peu enigmatique....
#23 - 01-09-2012 12:06:59
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
checs 13
Christian91 a écrit:nodgim a écrit:Je reviens sur mon raisonnement d'origine ...
Voilà à peu près mon raisonnement.
Je suis curieux de voir ce que sera la solution complète ...
Bien sûr qu'en ne lisant que le début et la fin...
#24 - 01-09-2012 12:19:11
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 5,996E+3
Echecss 13
nodgim a écrit:"Si une flèche permet de rejoindre cette boucle, c'est qu'on peut en trouver une plus petite en passant par cette case donc ou que cette case ne peut pas être atteinte."
Phrase un peu enigmatique....
Bah non. Si une case au centre de la boucle permet de rejoindre la boucle, c'est qu'on n'est pas sur la boucle minimale.
Soit elle appartient à un trajet qui permet de réduire la boucle, soit elle appartient à un trajet auquel rien ne mène (une impasse à reculons en quelque sorte).
Après, si on raisonne comme ça sur chaque case à l'intérieur de la boucle toutes les cases ne peuvent quand même pas venir de nulle part vu que chacune doit mener quelque part.
Mais j'aurais peut-être du rajouter les flèches extérieures à la boucle.
On voit aussi qu'il est impossible de rentrer dans la boucle sans l'emprunter.
#25 - 01-09-2012 12:37:01
- Christian91
- Passionné de Prise2Tete
- Enigmes résolues : 0
- Messages : 89
- Lieu: 91
Ehecs 13
nodgim a écrit:Christian91 a écrit:nodgim a écrit:Je reviens sur mon raisonnement d'origine ...
Voilà à peu près mon raisonnement.
Je suis curieux de voir ce que sera la solution complète ...
Bien sûr qu'en ne lisant que le début et la fin...
éh j'ai tout lu, ce n'est qu'une ellipse ! Ou bien tu es très drôle et je me suis fait avoir.
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum










