Forum dédié aux énigmes et à toutes formes de jeux de logique. | Déconnexion |
|
Tu n'es pas identifié sur Prise2tete : s'identifier.  Accueil Accueil
 Forum Forum
|
 |
#1 - 10-01-2013 22:29:59
Géométrie pour les nusl (12)Allez une valeur sur cette fois ci, "L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
#0 Pub#2 - 10-01-2013 22:40:49
Géométrie our les nuls (12)Je ne sais pas dessiner sur ce site #3 - 10-01-2013 22:50:44
Géométrie pour les nul s(12)C'est un grand classique mais amusant #4 - 11-01-2013 01:43:05
géométrie poyr les nuls (12)On remarque tout d'abord qu'un triangle a toujours au moins une hauteur dont la base appartient au coté. Pour s'en convaincre, on remarque qu'un triangle a toujours au moins 2 angles aigus, la hauteur issue de l'autre sommet coupe la base à l'intérieur du triangle. #5 - 11-01-2013 01:54:38
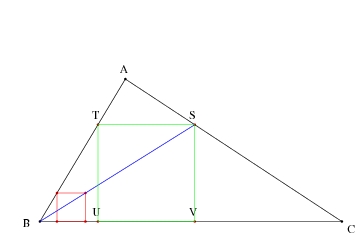
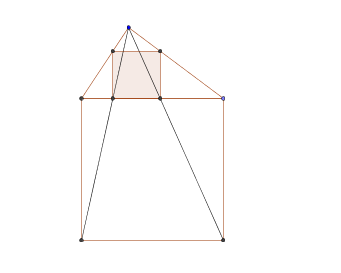
Géométtrie pour les nuls (12)Un coté du triangle est appelé base (on dira que cette base est horizontale). On considère l'ensemble des rectangles qui ont 2 sommets sur la base et 1 sommet sur chacun des 2 autres cotés. Parmi ces rectangles, on passe continument d'un rectangle aplati horizontal à un rectangle aplati vertical, et donc on passe par un carré à un moment. #6 - 11-01-2013 09:52:02
géométrie piur les nuls (12)On trace un petit carré dans l'angle B. #7 - 11-01-2013 17:20:48#8 - 11-01-2013 18:18:26
Géométrie pou les nuls (12)Ben oui, ça parait évident. #9 - 11-01-2013 22:39:06
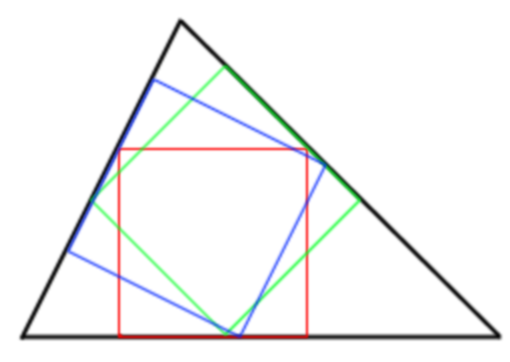
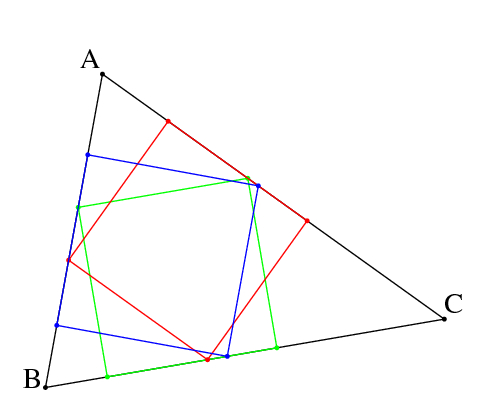
Gémoétrie pour les nuls (12)On peut même en construire 3 ! #10 - 12-01-2013 15:43:06#11 - 12-01-2013 16:07:20
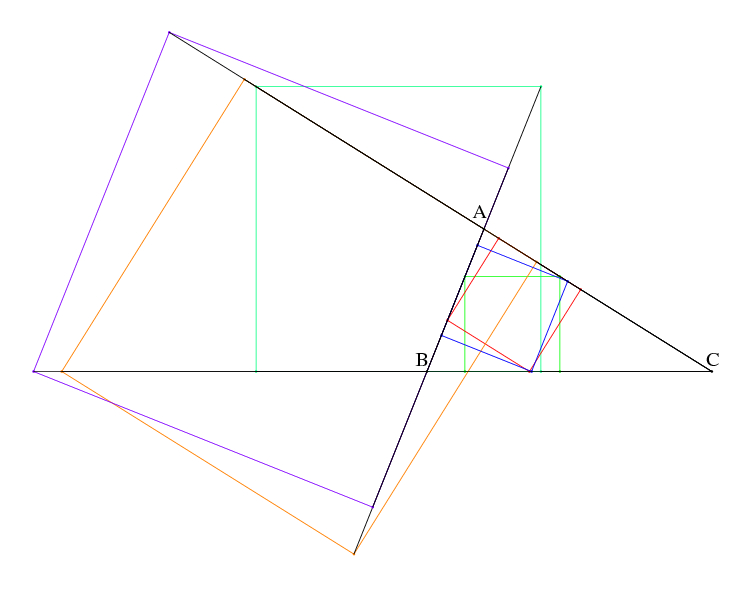
Géométrie pour es nuls (12)Encore des bonnes que réponses, @masab les quatres points sont sur le triangles pas sur des prolongement des côtés, mais sinon c'est juste "L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline #12 - 12-01-2013 16:12:57
géomérrie pour les nuls (12)En prenant comme base le plus grand côté, il suffit de faire descendre une parallèle à ce côté depuis le sommet opposé jusqu'à ce que sa largeur (croissante ) soit égale à sa hauteur (décroissante ) . #13 - 12-01-2013 16:32:37
Géométrie pour les nuls (12))Soit un triangle. #14 - 13-01-2013 10:27:53#15 - 14-01-2013 19:51:38#16 - 14-01-2013 21:52:22
Géométriee pour les nuls (12)Question (à laquelle #17 - 14-01-2013 22:32:58#18 - 16-01-2013 11:51:08
Géométrie pour les nuls (12))On considère un triangle ABC. #19 - 16-01-2013 18:10:46
Géométrie pour les nusl (12)
Une boucle pas forcément convexe ? #20 - 16-01-2013 19:07:32#21 - 16-01-2013 20:29:12#22 - 17-01-2013 14:46:26
Géométrie pour les nuuls (12)L'assertion "sur une boucle , il existe toujours quatre points formant un carré" est démontrée si la courbe possède une tangente en tout point et si cette dernière varie continûment ; autrement dit si la courbe est de classe C1. #23 - 17-01-2013 14:57:51#24 - 17-01-2013 15:50:31
Géométrie pour les nulls (12)
Pour [latex]{h_A} = \frac{2S}{a}[/latex] j'ai compris. Mais d'où sors tu la première égalité ? #25 - 17-01-2013 17:47:58
géométrie pour kes nuls (12)Pour prouver la 1ère égalité, il suffit d'écrire que l'aire de ABC est égale à l'aire du carré plus l'aire de 3 triangles. Avec les notations de ma 1ère figure Réponse rapideSujets similaires
Mots clés des moteurs de recherche |
 | |||||||||||||||||||||||||||||||||
| Prise2Tete Forum Statistiques Liste des membres Hall of Fame Contact | |||||||||||||||||||||||||||||||||||
Un jeu où seules la réflexion, la logique et la déduction permettent de trouver la solution.