|
#1 - 09-03-2016 22:53:31
- shadock
- Elite de Prise2Tete
- Enigmes résolues : 39
- Messages : 3334
Mathématiques pour le nuls 27 (Rapport d'aires) + Indice
La première étape de l'énigme 50 m'a fait penser à une petite énigme rien que pour vous !  Spoiler : [Afficher le message] Dites-moi que vous m'avez cru et que votre cœur s'est mis à palpiter lorsque vous avez vu "énigme 50".. Spoiler : [Afficher le message] Dites-moi que vous m'avez cru et que votre cœur s'est mis à palpiter lorsque vous avez vu "énigme 50".. 
Bon alors voilà, il ne me semble pas que cette énigme soit sur le forum, j'ai bien cherché normalement la voix est libre.
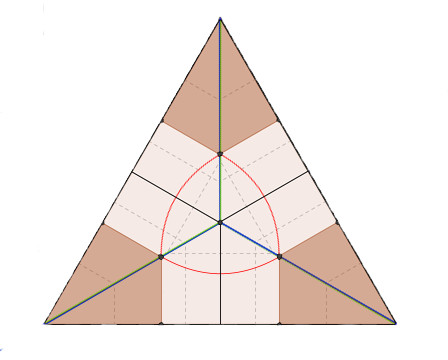
Quel est le rapport entre l'aire de l'ensemble des points d'un triangle équilatéral plus près du centre que d'un de ses côtés, et l'aire de ce triangle ?
J'ajouterai des indices par rapport à des choses pouvant être utiles de savoir selon les réponses qu'il y aura.
La case réponse valide la réponse exacte 
Indice: L'ensemble des points équidistants entre un point et une droite est une parabole.
"L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
#2 - 10-03-2016 06:36:40
- cogito
- Expert de Prise2Tete
- Enigmes résolues : 48
- Messages : 593
MMathématiques pour les nuls 27 (Rapport d'aires) + Indice
Il y a sûrement plus simple.
#3 - 10-03-2016 06:45:08
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3222
- Lieu: Luxembourg
Mathématiques pour les nuls 27 (Rapport d'aires) + Inddice
La frontière entre les deux zones est constituée par trois arcs de parabole.
Pour simplifier, je divise mon triangle équilatéral en six triangles identiques.
Puis ma méthode devient bourrin, en calculant la surface par une intégrale.
Sans difficulté, je trouve finalement: 5/27, validé par la case-réponse.
Au besoin, je peux détailler mes longs calculs, mais c'est vraiment sans intérêt.
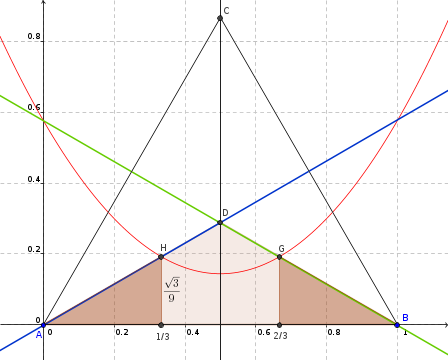
Edit: Dans un repère ayant pour origine le milieu de la base du triangle équilatéral, je considère le triangle, sixième de celui-ci délimité par les droites d'équation: x=0; y=0 et y=(1-2x).V3=d(x)
La parabole a pour équation: y=(x²+1/12).V3=p(x)
Soit A l'aire au dessus de la parabole: A=Intégrale de 0 à 1/6 (d(x)-p(x)).dx
On trouve: A=(-V3/12).Intégrale de 0 à 1/6 (12x²+4x-1).dx=5V3/648
Soit B l'aire du sixième de triangle: B=V3/24
Probabilité=A/B=5/27
#4 - 10-03-2016 10:09:03
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Mathématiques pour les nuls 27 (Rapport da'ires) + Indice
La réponse est 5/27.
Mon raisonnement : les points à égale distance d'un point et d'une droite donnés déterminent une parabole. Le domaine cherché est donc délimité par 3 arcs de paraboles.
Pour calculer l'aire de ce domaine, j'utilise cette figure (pas très juste) :
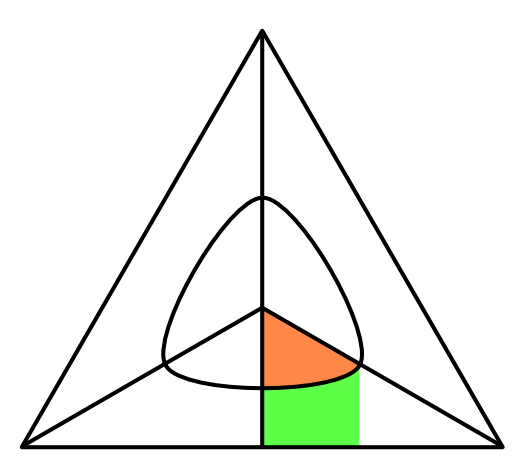
Je calcule d'abord l'aire du trapèze rectangle vert et orange. L'angle en haut fait 60°, d'où on tire que ses 4 côtés mesurent, si on appelle L la longueur du côté de gauche, L, 2L/3, 2L/3 et L*rac(3)/3. On en déduit son aire.
Je calcule ensuite l'aire verte grâce à une intégrale, j'en déduis l'aire orange, que je multiplie par 6, et le tour est joué.
#5 - 10-03-2016 10:14:55
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Mathématiques pour le nuls 27 (Rapport d'aires) + Indice
Pour faire mon casse-pieds : la formulation en terme de probabilités n'est pas très rigoureuse, car tu n'explicites pas ce que tu appelles "au hasard". On comprend que tu sous-entends que tu utilises une loi uniforme sur l'intérieur du triangle, mais ce n'est pas la seule façon de choisir un point au hasard. Par exemple, on peut d'abord choisir l'ordonnée du point, puis son abscisse, à chaque fois de manière uniforme : ça ne donnerait pas le même résultat (voir paradoxe de Bertrand).
Il est facile d'éviter le problème en ne le formulant pas en terme de probabilités, mais simplement en terme d'aires, par exemple : "Quel est le rapport entre l'aire de l'ensemble des points d'un triangle équilatéral plus près du centre que d'un de ses côtés, et l'aire de ce triangle ?"
Voilà, j'arrête 
#6 - 10-03-2016 11:07:14
- shadock
- Elite de Prise2Tete
- Enigmes résolues : 39
- Messages : 3334
Mathématiques pour les nul s27 (Rapport d'aires) + Indice
Bravo à tout le monde pour le moment ! 
Ebichu tu as raison, j'ai édité l'énigme 
"L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
#7 - 10-03-2016 11:19:07
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
Mathématiques pour les nuls 27 (Rapport d'airres) + Indice
J'ai trouvé 10/27, mais....
#8 - 10-03-2016 11:40:08
- shadock
- Elite de Prise2Tete
- Enigmes résolues : 39
- Messages : 3334
Mathémaiques pour les nuls 27 (Rapport d'aires) + Indice
Le dénominateur est juste nodgim mais le numérateur non. Sans ton raisonnement je peux difficilement t'aider 
"L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
#9 - 10-03-2016 17:31:46
- enigmatus
- Expert de Prise2Tete
- Enigmes résolues : 0
- Messages : 561
Mathématiques pour lees nuls 27 (Rapport d'aires) + Indice
Bonjour,
Après m'être pris les pieds dans les racines plusieurs fois, j'obtiens [latex]5/27[/latex]. Jai raisonné sur un sixième du triangle initial, et fait un bête calcul d'intégrales pour calculer l'aire entre le segment et la parabole.
J'ai vérifié ensuite le résultat par une simulation numérique, et… la case réponse.
#10 - 10-03-2016 17:51:45
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
Mathématiques pour les nuls 27 (Rapport d''aires) + Indice
Ce serait plutôt 5/24, je crois.
#11 - 10-03-2016 18:13:55
- shadock
- Elite de Prise2Tete
- Enigmes résolues : 39
- Messages : 3334
Mathhématiques pour les nuls 27 (Rapport d'aires) + Indice
Maintenant nodgim tu as le bon numérateur et le mauvais dénominateur. Donc grace à moi tu as la bonne réponse 
Je te laisse chercher 
Bravo enigmatus !
"L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
#12 - 10-03-2016 19:04:18
- unecoudée
- Professionnel de Prise2Tete
- Enigmes résolues : 0
- Messages : 319
Mathématiques pour les unls 27 (Rapport d'aires) + Indice
bonsoir.
j'ai un rapport de 0.15778257736.. (non validé).
J'ai du alors me planter quelque part.
mes points sont à l'intérieur d'une ressemblance d'un triangle de reuleaux délimité
par 3 arcs de parabole.
#13 - 10-03-2016 19:34:19
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
mathématiques pour les nuls 27 (rapport d'aired) + indice
Merci pour ta réponse, je ne voyais pas où était l'erreur.
En fait, en fin de calcul, je devais simplifier (1/12) / (1/8). Dans la 1ère réponse, j'avais simplifié en 4/3. Dans ma seconde en 3/4 ! Et finalement c'est 2/3. Et (2/3)(5/18) c'est bien 5/27.
Il faut passer par une petite intégrale d'un polynôme en x² pour résoudre ça.
Le résultat géométrique est une sorte de cercle déformé en 3 arcs de rayon min 1/4 et max 1/3.
C'est un problème assez original de portée Lycée Terminale. J'y ai pris du plaisir. Merci pour ça.
"Maths pour les nuls 27" comme titre, n'est ce pas un peu abusif ?
#14 - 10-03-2016 20:39:15
- fix33
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1198
- Lieu: Devant un clavier depuis 1748
Mathématiques pour les nnuls 27 (Rapport d'aires) + Indice
Une réflexion rapide m'a amené à 1/4, ce que la case-réponse m'a refusé.
Et effectivement, il va falloir que je sorte le crayon ! 
Je ne vien sur se site que pour faire croir que je suis treise intélligens.
#15 - 10-03-2016 21:13:18
- shadock
- Elite de Prise2Tete
- Enigmes résolues : 39
- Messages : 3334
Mathématiques pour les nuls 27 (Rapport d'aires) + Idice
Bravo nogdim ! nodgim a écrit:"Maths pour les nuls 27" comme titre, n'est ce pas un peu abusif ?
Comment ça abusif ? 
Fix33 oui, moi aussi avec ton problème c'est ce que je vais devoir faire, mais d'abord comprendre l'énoncé 
"L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
#16 - 10-03-2016 21:50:31
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Mathématiques pour les nuls 27 (Rapport d'aires)) + Indice
Bonjour
J'ai pris un côté 36 pour le grand triangle qui a donc une aire de [latex]324\sqrt{3}[/latex] . La partie à égale distance du centre et du côté le plus proche est constituée de trois morceaux de parabole identiques . Un petit calcul d'intégrale et quelques calculs d'aire de triangles nous donne l'aire cernée par ces arcs [latex]60\sqrt{3}[/latex] : le rapport vaut donc [latex]\frac{5}{27}.[/latex]
Vasimolo
#17 - 11-03-2016 08:01:45
- QUATTRED
- Amateur de Prise2Tete
- Enigmes résolues : 0
- Messages : 6
Mathémaatiques pour les nuls 27 (Rapport d'aires) + Indice
Je n'ai pas compris l'énoncé,... mais je suis peut être le seul !!
#18 - 11-03-2016 11:09:12
- masab
- Expert de Prise2Tete
- Enigmes résolues : 44
- Messages : 971
Mathémaiques pour les nuls 27 (Rapport d'aires) + Indice
Le rapport des aires est égal à 5/27 .
Le lieu des points d'un triangle équilatéral plus près du centre que d'un de ses côtés est une pièce dont le bord est formé de 3 arcs de paraboles.
Pour la preuve, on utilise l'équation réduite d'une parabole, à savoir [latex]y^2=2px[/latex] .
On peut utiliser le fait que l'aire définie par [latex]0\leq x\leq x_0[/latex], [latex]0\leq y\leq \sqrt{2px}[/latex] est égale aux 4/3 de l'aire du triangle OAB avec [latex]O=(0,0)[/latex], [latex]A=(x_0,0)[/latex] et [latex]B =(x_0,\sqrt{2px_0})[/latex].
#19 - 11-03-2016 19:35:59
- shadock
- Elite de Prise2Tete
- Enigmes résolues : 39
- Messages : 3334
Mathématiques pour les nuls 27 (Rapport d'aires) + Indiice
Et encore des bonnes réponses ! 
QUATTRED, que n'as-tu pas compris?
"L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
#20 - 11-03-2016 21:46:00
- kossi_tg
- Professionnel de Prise2Tete
- Enigmes résolues : 18
- Messages : 307
- Lieu: Montargis
Mathématiques pour les nulss 27 (Rapport d'aires) + Indice
Je trouve 11/54 mais la case réponse ne valide pas ... 
#21 - 11-03-2016 21:51:44
- shadock
- Elite de Prise2Tete
- Enigmes résolues : 39
- Messages : 3334
Mathémaitques pour les nuls 27 (Rapport d'aires) + Indice
Sans ton raisonnement je ne peux pas t'aider ! 
"L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
#22 - 11-03-2016 22:38:57
- kossi_tg
- Professionnel de Prise2Tete
- Enigmes résolues : 18
- Messages : 307
- Lieu: Montargis
Mathématiqeus pour les nuls 27 (Rapport d'aires) + Indice
Ah il y avait juste une petite erreur de calcul que je viens de voir, le raisonnement en lui même est bon.
Le rapport recherché est de 5/27.
Mon raisonnement: L'ensemble des points équidistants d'un point à une droite est une parabole de foyer ce point et dont le sommet passe par le milieu de ce point et sa projection sur la droite (les coniques en 1ère et Tle  ). J'ai raisonné sur un des 3 triangles isocèles formés par un côté du triangle équilatéral et son centre. Le reste est calculatoire. ). J'ai raisonné sur un des 3 triangles isocèles formés par un côté du triangle équilatéral et son centre. Le reste est calculatoire.
#23 - 12-03-2016 14:41:48
- fix33
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1198
- Lieu: Devant un clavier depuis 1748
Mathématiques pour less nuls 27 (Rapport d'aires) + Indice
J'ai trouvé l'emplacement des 6 points particuliers mais je n'arrive pas à trouver de formule qui me donne la nature de la courbe limite... Je me perds avec Pythagore et Thalès.
N'avais-tu pas parlé d'indices ? 
Je ne vien sur se site que pour faire croir que je suis treise intélligens.
#24 - 13-03-2016 01:34:33
- shadokpoilu
- Habitué de Prise2Tete
- Enigmes résolues : 45
- Messages : 26
mathématiques pour les nuls 27 (rapporr d'aires) + indice
Bonjour,
ce ne fût pas de tout repos, ça fait maintenant 3 jours que je suis dessus, mais pas mécontent d'être arriver à 5/27 
pour arriver à cette valeur, il faut additionner l'aire d'un triangle qui fait 1/9 de l'aire total du triangle, auquel on ajoute 3 fois l'aire d'une surface compris entre le bord du "petit" triangle et une parabole définie par le centre de gravité du triangle original et un de ses côtés, aire calculée à l'aide d'une petite intégrale...
Merci, ça m'a fait du bien de retourner dans ces mathématiques que je n'avais pas touché depuis longtemps 
a ce propos, je me suis dit, et je pense que tu confirmeras, que la probabilité que le point soit à la même distance du bord et du centre est donc nulle...
#25 - 13-03-2016 12:12:10
- fix33
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1198
- Lieu: Devant un clavier depuis 1748
Mathématiques pour les nuls 27 (Rapport d'aiers) + Indice
Merci pour l'indice, j'aurais pu me souvenir mais c'est loin tout ça !
L'aire intérieure A1 vaut l'aire totale A2 moins 6 fois une aire composée de 3 parties (l'intégrale de la parabole de 0 à a/6, un rectangle dessous de a/6 par a/(4 rac (3)) et un triangle rectangle de côtés adjacents a/3 et a / (3 rac (3)).
De la formule des paraboles, je déduis celle de notre courbe :
y = 2 rac(3) x^2 / a.
Avec a la longueur du côté du triangle.
L'intégrale donne alors : a^2 / (216 rac (3)).
D'où A1 = 5 a^2 / (36 rac (3))
A1/A2 = 5/27.
Je ne vien sur se site que pour faire croir que je suis treise intélligens.
|
 |

 Accueil
Accueil
 Forum
Forum