Bonjour !
Soit x la longueur (en mètres) du segment [AC], on a donc [CB] = 48-x
Le carré obtenu avec le bout [AC] a pour aire (x/4)²
Le triangle équilatéral obtenu avec le bout [CB] a pour aire (V3 /4)*((48-x)/3)²
(notation V= racine, j'ai la flemme et pas le temps pour du Latex)
La somme des deux aires est donc (1/16 + V3 /36) x² - (96 * V3 /36) x + V3 * 48²/36
appelons x -> f(x) cette fonction définie de R dans R
f(x) = (1/36) * [(9/4 + V3) x² - 96*V3 x + 2304*V3]
sa dérivé f' est :
f'(x) = (1/36) [2*(9/4+V3) x - 96V3]
Elle s'annule en x = 48 V3 / (9/4+V3) soit en x = 20,88 mètres ce qui correspond (je vous passe le tableau de variations) à un minimum de f valant 62,63 m²
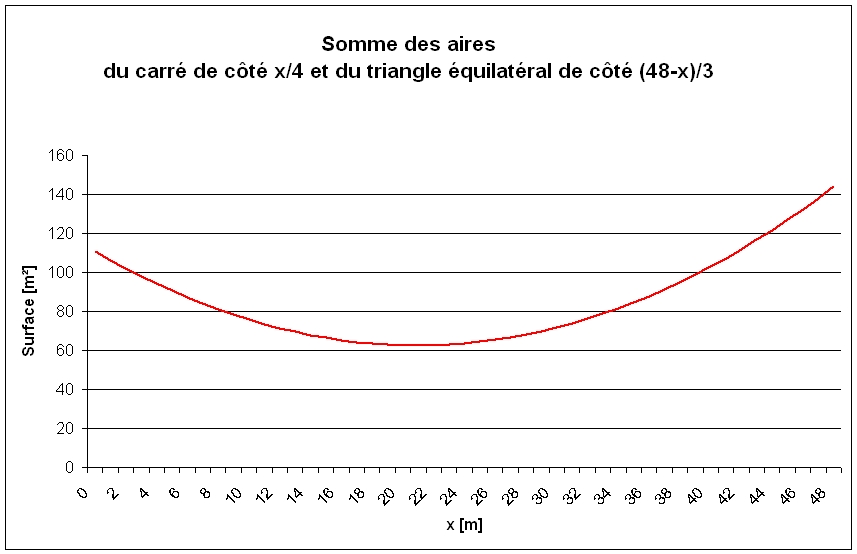
Le carré a alors une aire de : 27,24 m²
Le triangle équilatéral a alors une aire de : 35,39 m²
(Tiens sur le graphique on remarque que pour x= 48, i.e on fait seulement un carré l'aire vaut bien 144 m², normal ...)
Merci et à bientôt !

 Accueil
Accueil
 Forum
Forum