Je triche un peu

Il est connu que le plus grand triangle qu'on peut inscrire dans un cercle est le triangle équilatéral donc x=1/2 .

Vasimolo

Je préfère résoudre le problème en introduisant
[TeX]\alpha=\widehat{BOM}[/TeX]
Il suffit de varier cet angle entre 0 et pi pour décrire toutes les possibilités.
L'aire du triangle AMN est alors
[TeX]\mathcal A=\sin\alpha(1+\cos\alpha)[/TeX]
L'aire est maximale quand sa dérivée est nulle. Ce qui nous conduit à résoudre cette équation:
[TeX]2X^2+X-1=0[/latex], avec [latex]X=\cos\alpha[/TeX]
La solution qui nous intéresse est [latex]X=1/2[/latex].
L'aire est donc maximale quand h est entre O et B et quand
[TeX]x=\left|{X}\right|=1/2[/TeX]

avec [latex]x=\cos\theta[/latex], l'aire du triangle est   [latex](1+\cos\theta)\sin\theta[/latex]

que je derive [latex]-\sin^2\theta+(1+\cos\theta)\cos\theta=\cos^2\theta-1+\cos\theta+\cos^2\theta=2x^2+x-1=0[/latex]

qui donne
[TeX]x=\frac{-1\pm3}{4}=-1,1/2[/TeX]
j'en deduis que l'aire est maximale en 1/2. c'est le triangle equilateral.

et sinon l'aire vaut exactement [latex](x+1)\sqrt{1-x^2}[/latex]  que l'on peut aussi deriver en
[TeX]\sqrt{1-x^2}+(x+1)\frac12\frac{-2x}{\sqrt{1-x^2}}[/TeX]
qu'on multiplie par [latex]\sqrt{x^2-1}[/latex] (x=1,-1 n'etant certainement pas solution):

[latex](1-x^2)+(x+1)\frac12(-2x)=-2x^2-x+1[/latex]    qui ressemble pas mal au truc au dessus...

C'est pas une question d'analyse plutôt que d'algèbre ?
Logiquement le x est entre O et B pour sa valeur maximale.
On va dire que A est à droite et B à gauche.
Comme on est sur le cercle trigo, on associe un angle "a" entre Pi/2 et Pi aux valeurs de x tel que cos(a) = -x donc cos²(a) = x²

La base [NM] du triangle mesure 2*sin(a)
La hauteur [hA] mesure  x + 1/2
On note A(x) l'aire en fonction de x du triangle.
A(x) = Base*Hauteur/2 = (x+1/2)*sin(a) = (x+1/2)*racine(1-x²)

Là on dérive et on voit qu'on a un maximum quand -2x² -x/2 +1 s'annule, donc pour une valeur de x de ( -1 + racine( 33 ) ) / 8 si je ne m'abuse, ce qui donne un truc pas si loin de 5/8ème.

Dis moi si j'me plante ^^

C'est corrigé à priori, à moins d'une autre erreur.

Sympa ce p'tit problème !

Soit a l'angle MOB :


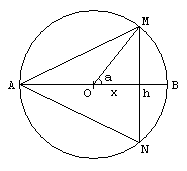
On cherche x = cos a

L'aire A du triangle AMN est :
A  =  (1/2 + cos a) * 2.sin a

On dérive cette fonction :
cos a + 2.cos² a - 2.sin² a
=  cos a + 2.(cos² a - sin² a)
=  cos a + 2.(1 - 2sin² a)
=  cos a + 2 - 4.sin² a
=  3 - 5.sin² a

Puis on cherche pour quelle valeur de a la dérivée est nulle :
3 - 5.sin² a  =  0
5.sin² a  =  3
sin² a  =  3/5
sin a  =  √(3/5)
a  =  arcsin( √(3/5) )

Ainsi, on en déduit x :
x  =  cos ( arcsin √(3/5) )

Ce qui nous donne une aire maximale de AMN pour x ≈ 0,63246
(soit un angle a ≈ 50,77°)


Remarque après coup :
Je viens de voir qu'en faisant mon dessin, sans connaître la réponse, j'ai placé h à un pixel près de sa position optimale ! Quel feeling
(en considérant bien sûr que je ne me sois pas gourré...)

On pose OH = x. L'aire du triangle AMN est base*hauteur = AH * MN+/2
Comme MHO est rectangle en H, que OH = x et que OM = 1, on a MH = racine (1-x^2)
Comme MH = HN et H sur [MN], MN = 2*racine(1-x^2)
Ensuite, on a deux cas.
1) H sur [OB] => AH = AO + OH = 1+x
Dans ce cas, l'aire vaut (1+x).racine(1-x^2).
Sa dérivée est racine(1-x^2)-(1+x)x/racine(1-x^2)
qu'on peut aussi écrire racine(1-x^2) [ 1+x/(x-1)]
On voit que la dérivée est positive si x < 1/2, donc l'aire admet un maximum en 1/2, qui vaut 3.racine(3)/4

2) H sur [OA] => AH  = OA-OH = 1-x

Dans ce cas, l'aire vaut (1-x).racine(1-x^2).
Sa dérivée est -racine(1-x^2)-(1-x)x/racine(1-x^2)
qu'on peut aussi écrire -racine(1-x^2) [1+x/(1+x)]
On voit que la dérivée est positive si x < -1/2, donc l'aire décroissante pour x compris entre 0 et 1, le maximum local est donc atteint en x=0 et l'aire vaut alors 1

Conclusion: le bon cas est le cas 1, H se situe au milieu de [OB] et l'aire vaut 3racine(3)/4

x: angle (Oh, OM).
Aire du triangle: sin(x)*cos(x) = sin(2x)/2

Dérivée: cos(2x)/2

Dérivée nulle et aire maximale: x=pi/4

Aire maximale: 1/2.

Il me semble que si la bonne réponse est [latex]x=\frac 12[/latex], la majorité des raisonnements sont incorrects. On ne peut exprimer l'aire de AMN en fonction de x, car à chaque [latex]x\neq 0[/latex] correpond deux points H possibles et distincts définissant deux triangles d'aires différentes.
Si l'on définit X comme l'abscisse de H dans un un repère orthonormé direct [latex] (O,\vec\imath,\vec\jmath)[/latex] avec [latex]\vec\imath=\vec{OB}[/latex], le raisonnement de Franck9525 fonctionne en remplaçant x par X (à condition de préciser les variations de A en fonction de x).
On conclue en disant que X=|x| donc un demi : lorsque l'aire est maximale, x vaut 0,5. (Mais la réciproque est fausse).

a*b
___
2
ca te dit rien?

Intuitivement il était évident que l'aire maximale était pour un triangle équilatéral. Cependant quand j'ai éssayé de faire les calculs par la dérivée (voir mon message plus haut), je trouve un point O en dehors du cercle.
Est-ce que quelqu'un peut me dire ou je me suis trompé?
Merci d'avance.

C'est la première fois que je plussois!