 |
#26 - 04-07-2013 21:07:41
- shadock
- Elite de Prise2Tete
- Enigmes résolues : 39
- Messages : 3334
Somme des angles dd'un polygône
Et alors où est le problème? Que faut-il modifier pour atteindre la perfection?
"L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
#27 - 05-07-2013 22:20:43
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
Somme des angles d'un plygône
Le problème, c'est qu'en faisant la même démonstration avec un pentagone, tu montres que la somme des angles d'un pentagone fait 180°. Embêtant non ?
As-tu maintenant compris où se situe le problème ?
#28 - 05-07-2013 22:37:10
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
Somme des angles d'un poygône
Franky1103 a écrit:Complément plus détaillé
Je prend un point intérieur au polygone à n côtés et je dessine les n triangles associés en joignant ce point central aux n sommets.
Soient Ai les angles "centraux" de ces n triangles. La somme des angles Ai (i variant de 1 à n) vaut 360° (tour complet) et la somme des deux autres angles de chaque triangle vaut 180° - Ai.
Donc la somme des angles du polygone est la somme des (180° - Ai), ou encore la (somme des 180° - somme des Ai), soit 180.n - 360.
gwen27 a écrit:(n-2)x180°
Vu qu'en partant d'un sommet on peut tracer n-2 traits vers un autre sommet non contigu, on définit n-2 triangle dont la somme des angles est 180°.
SabanSuresh a écrit:J'ai trouvé ! En fait la somme des angles d'un polygone à n côtés vaut 180(n-2) car on peut y "loger" n-2 triangles délimités par des diagonales de ce polygone.
cogito a écrit:Pardon, j'avais oublié le cas général  : :
Pour un polygone à n coté la somme des angles est (n - 2) * 180.
Pour s'en rendre compte on peut relié un sommet à tous les autres, et on voit apparaître (n - 2) triangles et la somme des angles de ces (n-2) triangles est
la somme des angles du polygone .
dylasse a écrit:Appelons S(n) la somme des angles d'un polygone à n coté.
Dans un polygone à n cotés, on choisit un angle <180° (il y en a un, sinon, le polygone possède une drôle de tête... euh... je sais l'argument est maigre !), correspondant au sommet Q.
On relie ensemble les 2 sommets (P et R) voisins du précédents, on obtient un polygone de somme d'angle S(n-1). Le triangle PQR a une somme d'angle égale à 180° et on a donc la relation S(n)=S(n-1)+180
Cette relation de récurrence nous conduit à S(n) = 180 (n-2), valable pour n>=3.
Ces démonstrations ne sont pas valables pour un polygone non convexe.
#29 - 05-07-2013 23:17:18
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
somme des angles f'un polygône
Alexein41 a écrit:Pour un polygone non convexe :
J'appelle S1, S2, S3, S4, ..., Sn les n sommets du polygone Pn.
Enfin, je suppose sur Pn que [S1S3] n'appartient pas au polygone Pn. Pn est donc non convexe (problème "en S2").
Je prends un point T dans le plan tel que :
- le polygone S1.T.S3.S4...Sn.S1 soit non croisé ;
- T n'appartienne pas à [S1S3] ;
- la diagonale [S1S3] appartienne au polygone S1.T.S3.S4...Sn.S1.
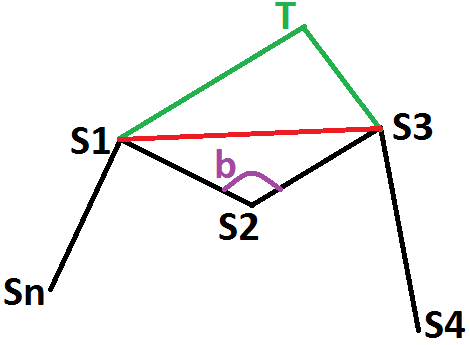
Est-ce que ce point T existe toujours ? Et s'il y avait un autre point du polygone dans le triangle S1S2S3 ?
#30 - 05-07-2013 23:59:07
- Alexein41
- Professionnel de Prise2Tete
- Enigmes résolues : 29
- Messages : 119
Somme des angls d'un polygône
titoufred a écrit:Est-ce que ce point T existe toujours ? Et s'il y avait un autre point du polygone dans le triangle S1S2S3 ?
Le caractère de ta première question est purement oratoire, le contre-exemple le prouvant étant dans la seconde question.
Je pense néanmoins que ma démonstration est adaptable en tenant compte de ce cas de figure. Si j'avais une ébauche de preuve à fournir, je dirais que localement (ie. "en les points" où le polygone est non convexe), "la somme des angles" n'est pas changée par transformation via le point T, que ce soit d'un côté du polygone, ou de l'autre. On pourrait alors se ramener au cas convexe.
Je ne terminerai pas ni ne détaillerai les explications ou la fin de cette démonstration si tenté qu'elle soit effectivement commencée, je concèderais volontiers que cette ébauche n'est pas correcte si elle n'est pas correcte, je reconnais donc que mes limites sont atteintes pour ce problème et j'admets mon erreur.
#31 - 06-07-2013 00:22:47
- shadock
- Elite de Prise2Tete
- Enigmes résolues : 39
- Messages : 3334
somme des angles d'un pplygône
Ah oui Titou je suis d'accord avec toi  , mais dans le cas d'un triangle il n'y a pas de problème puisque c'est le "plus petite" figure géométrique que l'on puisse tracer à la règle. Evidemment ce n'est pas d'une rigueur parfaite mais pour le triangle c'est suffisant. , mais dans le cas d'un triangle il n'y a pas de problème puisque c'est le "plus petite" figure géométrique que l'on puisse tracer à la règle. Evidemment ce n'est pas d'une rigueur parfaite mais pour le triangle c'est suffisant.
PS : La démonstration vient de mon prof de première S, on avait fait un exo en cours, donc il faut croire que la communauté mathématique accepte des petites imprécisions, du moment que le raisonnement est simple et concret si je puis dire ainsi.
Shadock 
"L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
#32 - 06-07-2013 01:06:52
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
somme des abgles d'un polygône
Alexein41 a écrit:Je pense néanmoins que ma démonstration est adaptable en tenant compte de ce cas de figure. Si j'avais une ébauche de preuve à fournir, je dirais que localement (ie. "en les points" où le polygone est non convexe), "la somme des angles" n'est pas changée par transformation via le point T, que ce soit d'un côté du polygone, ou de l'autre. On pourrait alors se ramener au cas convexe.
Je n'ai pas trop compris l'argument. On se retrouve avec un polygone croisé et l'on ne peut appliquer la récurrence non ?
shadock a écrit:Ah oui Titou je suis d'accord avec toi, mais dans le cas d'un triangle il n'y a pas de problème puisque c'est le "plus petite" figure géométrique que l'on puisse tracer à la règle. Evidemment ce n'est pas d'une rigueur parfaite mais pour le triangle c'est suffisant.
PS : La démonstration vient de mon prof de première S, on avait fait un exo en cours, donc il faut croire que la communauté mathématique accepte des petites imprécisions, du moment que le raisonnement est simple et concret si je puis dire ainsi.
La communauté mathématique n'accepte pas de petites imprécisions. Soit on est convaincu, soit on ne l'est pas. Pour l'instant, tu ne m'as pas encore convaincu. Soit ton prof de première S a donné un argument supplémentaire pour conclure et tu es passé à côté. Soit il ne l'a pas fait, et il a commis une erreur.
#33 - 06-07-2013 01:32:42
- shadock
- Elite de Prise2Tete
- Enigmes résolues : 39
- Messages : 3334
Somme des anglse d'un polygône
L'argument il l'a certainement donné mais je ne m'en rappelle pas et je ne vois pas lequel pourrait confirmer que ce que je dis est juste. Aurais-tu une idée?
"L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
#34 - 06-07-2013 08:48:45
- Alexein41
- Professionnel de Prise2Tete
- Enigmes résolues : 29
- Messages : 119
Some des angles d'un polygône
titoufred a écrit:Je n'ai pas trop compris l'argument. On se retrouve avec un polygone croisé et l'on ne peut appliquer la récurrence non ?
Effectivement. Mais l'idée n'était pas tant d'appliquer la récurrence, plutôt de considérer que localement, si l'un des points (S2) d'un polygone le rend non convexe, alors la somme des trois angles SnS1S2 ; S1S2S3 ; S2S3S4 est équivalente à la même somme avec le point T, en oubliant tout le reste du polygone. J'ai bien conscience que ce n'est ni précis ni rigoureux, mais franchement, je n'ai pas d'autres idées...
#35 - 06-07-2013 13:51:59
- cogito
- Expert de Prise2Tete
- Enigmes résolues : 48
- Messages : 593
Somme de sangles d'un polygône
En fait ce qu'a montrer Alexein41 c'est que si il n'y a pas d'autre point du polygone
dans S1S2S3 alors on peut déplacer le point S2 sans changer la somme des angles du polygone. Autrement dit si on déplace les sommets d'un polygone sans créer de croisement alors on ne change pas la somme des angles de ce polygone.
On peut donc toujours se ramener au cas convexe.
Il y a sûrement plus simple.
#36 - 06-07-2013 22:32:12
- Alexein41
- Professionnel de Prise2Tete
- Enigmes résolues : 29
- Messages : 119
Somme des angles d''un polygône
Oui, en effet en fait ! Je préfère me dire que j'ai montré ce cas de figure-ci plutôt que me dire que je me suis complètement planté au cas non convexe ! 
#37 - 06-07-2013 22:59:48
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 5,996E+3
somme ded angles d'un polygône
titoufred a écrit:Ces démonstrations ne sont pas valables pour un polygone non convexe.
Bien sûr que si ... on peut partager un polygone non convexe en triangles convexes.

Et il y en a forcément n-2 par rapport aux sommets.
#38 - 06-07-2013 23:58:27
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Somme des angles dun polygône
Je n'ai pas tout lu mais il me semble que le problème se résume à : tout polygone non croisé à n côtés est-il décomposable en n-2 triangles ?
Pour les croisés c'est plus compliqué car certains angles des triangles ne font pas parti des angles du n-gone .

Vasimolo
#39 - 07-07-2013 20:40:53
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 5,996E+3
Smme des angles d'un polygône
#40 - 07-07-2013 23:28:33
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
somme des zngles d'un polygône
Je serai assez curieux de voir comment on montre l'existence de deux oreilles ou même d'une seule dans le cas d'un polygone simple ( non croisé ) .
Après une petite récurrence permet de conclure 
Vasimolo
#41 - 08-07-2013 00:30:58
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
somme des zngles d'un polygône
gwen27 a écrit:(n-2)x180°
Vu qu'en partant d'un sommet on peut tracer n-2 traits vers un autre sommet non contigu, on définit n-2 triangle dont la somme des angles est 180°.
titoufred a écrit:Cette démonstration n'est pas valable pour un polygone non convexe.
gwen27 a écrit:Bien sûr que si ... on peut partager un polygone non convexe en triangles convexes.

Et il y en a forcément n-2 par rapport aux sommets.
gwen, cette démonstration n'est pas du tout la même que celle que tu donnais dans ton premier message. Toi, tu parlais de n-2 traits partant du même sommet, ce qui n'est pas du tout le cas dans la méthode de triangulation (méthode des oreilles) donnée dans ton deuxième message. Ta première démonstration n'était donc pas valable. La démonstration de la triangulation par la méthode des oreilles est donnée ici : http://webcourse.cs.technion.ac.il/2366 … ters75.pdf
#42 - 08-07-2013 00:41:40
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
oSmme des angles d'un polygône
shadock a écrit:L'argument il l'a certainement donné mais je ne m'en rappelle pas et je ne vois pas lequel pourrait confirmer que ce que je dis est juste. Aurais-tu une idée?
Oui, il suffit de dire que tous les angles d'un triangle sont strictement inférieurs à 180°, donc la somme de ces angles est strictement inférieure à 540°. Comme tu as prouvé que cette somme est congrue à 180° modulo 360°, alors elle vaut 180°.
#43 - 08-07-2013 01:07:19
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
Somme de sangles d'un polygône
cogito a écrit:En fait ce qu'a montrer Alexein41 c'est que si il n'y a pas d'autre point du polygone
dans S1S2S3 alors on peut déplacer le point S2 sans changer la somme des angles du polygone. Autrement dit si on déplace les sommets d'un polygone sans créer de croisement alors on ne change pas la somme des angles de ce polygone.
Oui, Alexein a prouvé la propriété dans le cas où tous les sommets S2 où il y a un problème de convexité sont tels que S1S2S3 ne contient pas d'autre point du polygone. C'est le cas pour les polygones étoilés par exemple.
cogito a écrit:On peut donc toujours se ramener au cas convexe.
Il faudrait prouver pour conclure (dans le cas général d'un polygone quelconque non croisé) qu'il y a toujours un tel sommet S2 dans un polygone non convexe. Cela me semble être le cas.
#44 - 08-07-2013 18:30:28
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
spmme des angles d'un polygône
Moi, il me semble que c'est bien plus simple de dire qu'un petit bonhomme fait un tour complet et de comparer, dans le cas général, au franchissement d'un sommet quelconque, la déviation du petit bonhomme et l'angle intérieur au sommet.
#45 - 08-07-2013 19:50:31
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
Somme des anglees d'un polygône
Oui nodgim, mais la difficulté avec les angles orientés, c'est qu'à priori les égalités obtenues le sont modulo 360°.
#46 - 08-07-2013 21:09:37
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 5,996E+3
somme des zngles d'un polygône
En gros on a une démonstration (compliquée pour les non croisés, certes) , et un contre exemple pour les croisés...
Tu attends quoi de plus ?
#47 - 08-07-2013 22:08:45
- cogito
- Expert de Prise2Tete
- Enigmes résolues : 48
- Messages : 593
Somme des nagles d'un polygône
Le fait que l'on ait un point dans S1S2S3 n'a pas vraiment d'importance , ce qui est important c'est que la somme des angles SnS1S2, S1S2S3, et S2S3S4 est la même que la somme des angles SnS1T, S1TS3, TS3S4.
En fait le but n'est pas d'appliquer une hypothèse de récurrence, mais de se ramener au cas convexe. Alexein41 à montrer que si on remplaçait le point S2 par le point T alors on ne change pas la somme des angles du polygone et on à réduit le nombre d'endroit où le polygone était non convexe.
Ce qui manque par contre dans la démonstration c'est que seul le cas où le "trou"
qui crée la "disconvexité" est un triangle, alors que cela pourrait être un autre polygone convexe. Mais dans ce dernier cas on peut y arrivé avec un raisonnement similaire.
Il y a sûrement plus simple.
#48 - 09-07-2013 01:03:10
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
Smme des angles d'un polygône
Cogito, après avoir remplacé S2 par T, on peut récupérer un polygone croisé. Je pense que ça pose problème non ?
#49 - 09-07-2013 09:16:22
- cogito
- Expert de Prise2Tete
- Enigmes résolues : 48
- Messages : 593
somme des angles d'un oolygône
Oui, je vois, on pourrait avoir un polygone qui "s'enroule" sur lui-même, et le fait
de remplacer les S2 par des T suffirait pas à le "déroulé". Pour cela il faudrait faire
ce remplacement d'une manière plus précise. Je pense qu'en choisissant le point T sur la droite S1S3 (et donc S1TS3 = 180), on peut trouver une procédure qui se termine par un polygone convexe non croisé, j'essaierais de détaillé plus tard.
Il y a sûrement plus simple.
#50 - 09-07-2013 14:59:49
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
somme des angmes d'un polygône
Je réfléchis à l'idée de nodgim, qui me semble bonne. Mais je ne connais pas l'outil mathématique adapté. Il faudrait quelque chose à mi-chemin entre l'angle géométrique et l'angle orienté de deux vecteurs. On veut pouvoir parler d'angles positifs ou négatifs, mais l'on ne veut pas du modulo 360°.
Je propose, pour une ligne polygonale fermée [latex]A_1,... ,A_n[/latex] de définir [latex]dev(A_k)[/latex] la déviation angulaire en un sommet [latex]A_k[/latex] par la mesure principale de l'angle orienté entre les vecteurs [latex]\overrightarrow{A_{k-1}A_k}[/latex] et [latex]\overrightarrow{A_k A_{k+1}}[/latex].
Remarque : avec les notations habituelles [latex]A_0=A_n[/latex] et [latex]A_{n+1}=A_1[/latex].
La déviation angulaire en un sommet est donc comprise strictement entre -180° et +180°. On peut alors considérer la somme des déviations en tous les sommets d'une ligne polygonale, qui vaudra, dans le cas d'un polygone non croisé, +360° si la ligne polygonale tourne dans le sens trigo et -360° sinon (*). En renommant les points, on peut considérer que l'on tourne dans le sens trigo, ce que l'on suppose pour la suite. Comme l'a dit nodgim, la déviation en un sommet [latex]A_k[/latex] vérifie alors
[TeX]dev(A_k) = 180° - \widehat{A_k}[/TeX]
Il conclut alors en en faisant la somme des déviations sur tous les sommets du polygone :
[TeX]\sum_{k=1}^n dev(A_k) = \sum_{k=1}^n 180°-\widehat{A_k} = +360°[/TeX]
Ce qui donne
[TeX]\sum_{k=1}^n \widehat{A_k}=(n-2)\times 180°[/TeX]
CQFD.
(*) Résultat intuitif qui doit normalement se démontrer... mais là je sèche. On peut penser à l'indice d'un point par rapport à un lacet (en analyse complexe).
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum








