 |
#1 - 05-09-2013 22:54:37
- kossi_tg
- Professionnel de Prise2Tete
- Enigmes résolues : 18
- Messages : 307
- Lieu: Montargis
Le vieux dossier de rGand-Père : N°3
Bonsoir à tous,
La réplique 
Le coté du carré ci-dessus est 40. Si AB=BC=10 et DE=EF=30 alors quelle est l'aire du trapèze ACFD?
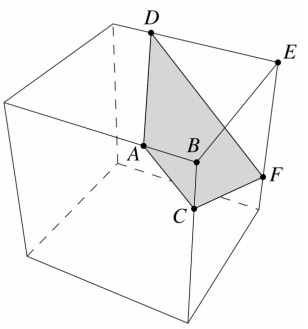
C'est parti pour 48h 
Réponse à valider avec 2 chiffres après la virgule. Cette fois, c'est bien une virgule qui sert de séparateur décimal... un peu d'habitude française 
#2 - 05-09-2013 23:42:32
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3230
- Lieu: Luxembourg
Le vieux dossier de Gand-Père : N°3
Je trouve respectivement:
AC=10V2 et DF=30V2
AD=CF=V(20²+40²)=20V5
Haut=V[(20V5)²-(10V2)²]=30V2
Aire=30V2*20V2=1200
mais ce n'est pas validé.
J'ai dû commettre une erreur.
Affaire à suivre.
#3 - 06-09-2013 00:15:57
- kossi_tg
- Professionnel de Prise2Tete
- Enigmes résolues : 18
- Messages : 307
- Lieu: Montargis
le vieux dossier de grand-pèee : n°3
Bravo Francky1103
Ca ne validait pas à cause d'une erreur dans ma case réponse où j'ai mis xx,,yy au lieu de xx,yy. Une virgule de trop, désolé 
#4 - 06-09-2013 15:13:38
- gabrielduflot
- Expert de Prise2Tete
- Enigmes résolues : 34
- Messages : 609
Le vieux dossir de Grand-Père : N°3
C'est un trapèze rectangle donc
A = (AC+DF)*CF/2
AC=10*rac 2
DF= 30* rac 2
CF= rac (40²+20²) = rac 2000 = 20 rac 5
A = 400 rac 10
si je ne me suis pas trompé dans les calculs
#5 - 06-09-2013 15:45:04
- kossi_tg
- Professionnel de Prise2Tete
- Enigmes résolues : 18
- Messages : 307
- Lieu: Montargis
Le vieux dossier de Gand-Père : N°3
gabrielduflot: Non, il doit avoir une erreur soit dans tes hypothèses de calcul soit dans tes calculs.
#6 - 06-09-2013 20:49:35
- cogito
- Expert de Prise2Tete
- Enigmes résolues : 48
- Messages : 593
Le vieux dossier d Grand-Père : N°3
Belle réplique ! 
Alors, l'aire du trapèze ACFD est (AC + FD) * h / 2 où h est la hauteur du trapèze.
On sait que AC=10√2 et que FD=30√2.
Il ne reste plus qu'a déterminer h.
Soit M le milieu de AC et N le milieu de FD.
Comme AB=BC et que EF=ED alors CF = AD, donc le trapèze ACFD est isocèle.
Cela signifie que MN est une hauteur du trapèze ACFD, en particulier MN=h.
Si M' et N' sont respectivement les projetés de M et de N sur la face opposé du cube, alors MM'NN' est un rectangle dont la diagonale MN = h.
On sait que MM'=40, il ne reste plus qu'a déterminer MN'.
Si l'on projetre également les points D et F sur la face opposé du cube, et que l'on regarde de face la face qui contient les points ABC, on a la figure suivante :
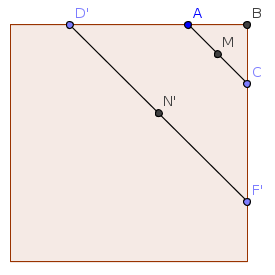
On a BM = AC/2 et BN' = F'D'/2 = FD/2 et donc MN' = BN' - BM = (FD - AC)/2.
autrement dit M′N=MN′=10√2.
Donc, Pythagore dans MM'N donne :
MN2=MM′2+M′N2=402+(10√2)2=1600+200=1800=302∗2
et donc h=MN=30√2
Donc finalement, l'air du trapèze ACDF est :
(AC+FD)∗h2=40√2∗30√22=1200
(Je n'ai pas fait les dessins en 3D avec les projections, donc j'espère que mon explication n'est pas trop confuse).
Il y a sûrement plus simple.
#7 - 06-09-2013 21:46:30
- kossi_tg
- Professionnel de Prise2Tete
- Enigmes résolues : 18
- Messages : 307
- Lieu: Montargis
Le vieux dossier de Garnd-Père : N°3
BRAVO cogito!
merci 
#8 - 06-09-2013 22:34:47
- shadock
- Elite de Prise2Tete
- Enigmes résolues : 39
- Messages : 3334
le vieux dossoer de grand-père : n°3
C'est l'aire de deux triangles de l'espace que l'on peut calculer très facilement avec un produit vectoriel comme suit :
On considère le point comme l'origine de notre repère donc B(0,0,0) on se déplace de manière à avoir des coordonnées positives dans le repère. On a donc :
A(10,0,0) D(30,0,40)
B(0,0,0) E(0,0,40)
C(0,10,0) F(0,30,40)
On a donc AADFC=AADC+AAFC
=||→AD∧→AC||2+||→CF∧→CA||2
=300+300
=600
Qui n'est pas validé par la case réponse il doit donc y avoir une erreur quelque part mais je ne vois pas laquelle, si tu peux me donner un petit coup de pouce... 
"L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
#9 - 07-09-2013 00:01:19
- kossi_tg
- Professionnel de Prise2Tete
- Enigmes résolues : 18
- Messages : 307
- Lieu: Montargis
Le vieux dossier d Grand-Père : N°3
shadock: effectivement, il y a une erreur au niveau du choix de tes triangles 
#10 - 07-09-2013 08:16:29
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,039E+3
me vieux dossier de grand-père : n°3
Je dirais 20 rac(2) x rac(1800) soit 1200 mais mes calculs me paraissent un peu trop élémentaires pour avoir bon 
#11 - 07-09-2013 10:41:39
- kossi_tg
- Professionnel de Prise2Tete
- Enigmes résolues : 18
- Messages : 307
- Lieu: Montargis
ke vieux dossier de grand-père : n°3
Oui gwen27, tu as BON. si tu peux juste expliquer ta démarche. merci
#12 - 07-09-2013 10:42:11
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
le vieux dossier de grznd-père : n°3
Le plus difficile est de calculer la hauteur du trapèze.
En projetant AC sur la face du fond, A'C' est à une distance facilement calculable de DF. La hauteur du trapèze est donc l'hypothénuse du triangle rectangle dont le grand coté est le coté du carré et le petit coté est la distance entre A'C' et DF.
J'ai trouvé H=30rac2
Aire: (30rac2+10rac2)/2 * 30rac2=1200.
#13 - 07-09-2013 12:44:01
- kossi_tg
- Professionnel de Prise2Tete
- Enigmes résolues : 18
- Messages : 307
- Lieu: Montargis
Le vieux dosssier de Grand-Père : N°3
OUI nodgim 
#14 - 07-09-2013 12:47:06
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
le vieux dossier de grabd-père : n°3
J'ai bien aimé la réponse avec 2 chiffres après la virgule...
#15 - 07-09-2013 13:50:31
- shadock
- Elite de Prise2Tete
- Enigmes résolues : 39
- Messages : 3334
Le veux dossier de Grand-Père : N°3
Normalement ça marche avec n'importe quels triangles... 
"L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
#16 - 07-09-2013 15:01:43
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,039E+3
le vieux dossier de grand-pèrr : n°3
C'est la hauteur multipliée par la moyenne des bases.
les bases : 30 rac(2) et 10 rac(2) (Pythagore) => 20 rac(2)
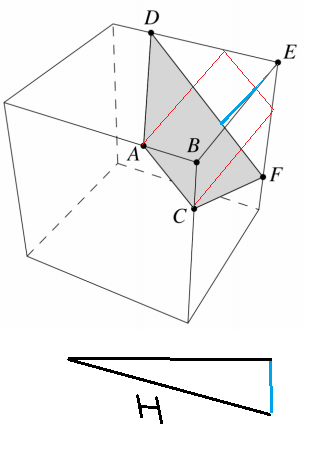
la hauteur : Je reporte ABC depuis E, le projeté est à angle droit. Donc Pythagore dit encore que la hauteur est (voire coupe )
H^2 = 40^2 + ( 30rac(2) -10rac(2) ) ^2
#17 - 07-09-2013 16:30:06
- kossi_tg
- Professionnel de Prise2Tete
- Enigmes résolues : 18
- Messages : 307
- Lieu: Montargis
Le vieux dossier de Grand-Prèe : N°3
gwen27: OK!
shadock: le problème ne vient pas du calcul sur un triangle mais du choix même de tes triangles. Le calcul est juste pour les triangles choisis mais est-ce les bons triangles? 
#18 - 07-09-2013 17:32:53
- shadock
- Elite de Prise2Tete
- Enigmes résolues : 39
- Messages : 3334
Le vvieux dossier de Grand-Père : N°3
J'ai bien compris, mais je ne voit pas en quoi le choix des triangles est important, j'ai divisé le trapèze en deux et... 
"L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
#19 - 07-09-2013 18:51:03
- halloduda
- Professionnel de Prise2Tete
- Enigmes résolues : 24
- Messages : 495
- Lieu: Ardèche
Le vieux dssier de Grand-Père : N°3
1200.00
Le trapèze isocèle est un triangle isocèle tronqué aux 2/3 de sa hauteur.
Son aire est 8/9 de l'aire du triangle.
La base est 30√2
les côtés du triangle isocèle = 3∗20√52=30√52
La hauteur du triangle isocèle = 45√2(Pythagore)
D'où l'aire S=8∗30√2∗45√29∗2=1200
#20 - 07-09-2013 20:10:29
- kossi_tg
- Professionnel de Prise2Tete
- Enigmes résolues : 18
- Messages : 307
- Lieu: Montargis
le vieux dosdier de grand-père : n°3
halloduda: BRAVO
shadock: et les triangles que tu as choisis couvrent bien la surface que tu veux calculer? Je n'en suis pas sûr  Tes 2 triangles se chevauchent, ce qui ne doit pas être le cas si tu divises vraiment le trapèze par deux. Tes 2 triangles se chevauchent, ce qui ne doit pas être le cas si tu divises vraiment le trapèze par deux.
|
 |

 Accueil
Accueil
 Forum
Forum









