 |
#1 - 19-10-2013 08:54:26
- Promath-
- Elite de Prise2Tete
- Enigmes résolues : 18
- Messages : 1416
- Lieu: Au fond de l'univers
qEuations du second degré
L'énigme m'a été posée par mon prof de maths, il ne s'agit ni d'un dm ni d'un exercice;
Y a t-il plus d'équations du second degré solvables dans R que non solvables dans R? Si non, quelle en est la fréquence?
J'ignore la réponse mais je cherche, la question me paraît suffisamment intéressante pour être soulevée.
Un promath- actif dans un forum actif
#2 - 19-10-2013 09:19:02
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3230
- Lieu: Luxembourg
equations du second drgré
"Y a t-il plus d'équations du second degré solvables dans R que non solvables dans R ?"
pourrait se traduire par:
"Je tire trois nombres A, B et C au hasard dans R et j'écris l'équation Ax²+Bx+c=0, y a t-il plus de chance que B²>4AC que B²<4AC ?", en remarquant que la probabilité que B²=4AC est nulle.
Je répondrais que c'est équiprobable (mais je peux me tromper).
Il y aurait donc autant d'équations du second degré solvables dans R que non solvables dans R.
#3 - 19-10-2013 09:33:48
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,039E+3
Equations d usecond degré
#4 - 19-10-2013 09:56:32
- ThomasLRG
- Habitué de Prise2Tete
- Enigmes résolues : 41
- Messages : 31
equations dy second degré
Bonjour,
Déjà c'est rigolo comme question !
je pars du principe qu'on parle des polynômes à coefficients réels. On peut se ramener à l'étude des polynômes unitaires en factorisant par le coefficient dominant.
Un polynôme du second degré unitaire "solvable" dans R s'écrit sous forme factorisée (x-x1)(x-x2). Il est caractérisé par ses 2 racines x1 et x2. On a donc bijection entre l'ensemble des polynômes du second degré unitaires avec l'ensemble des couples de réels (x,y) tels que x<=y (l'ordre empêche la double apparition du couple (x,y) et (y,x) ). Graphiquement cet ensemble est un demi-plan fermé, cet ensemble en bijection avec R² tout entier (je n'ai pas de bijection simple mais seulement par manipulation graphique, reste à en préciser une pour lever toute ambiguïté)
Un polynôme du second degré unitaire non "solvable" dans R est caractérisé par l'une de ses racines complexes puisque l'autre est son conjugué. Donc l'ensemble des polynômes du second degré unitaires non "solvable" dans R est en bijection avec RxR*+ (le premier R pour la partie réelle et R*+ pour la partie imaginaire qui doit être non nulle et positive pour ne pas compter 2 fois un complexe et son conjugué). Or R*+ est en bijection avec R par la fonction ln par exemple. Donc RxR*+ est en bijection avec R².
Finalement, l'ensemble des polynômes du second degré unitaires "solvable" dans R est en bijection avec ceux "non solvables" dans R. Il y en a donc "autant".
(reste a trouver une "bonne" bijection dans le premier cas)
Thomas.
edit : bijection de {(x,y) / x<=y} dans R² :
(x,y) -> (x,y-x) est une bijection de {(x,y) / x<=y} dans RxR+
or R+ est en bijection avec R*+ (on envoie chaque nombre entier sur son successeur) et R*+ est en bijection avec R par ln. D'où la bijection recherchée.
#5 - 19-10-2013 10:16:36
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
quations du second degré
Exactement 50%.
Visualise la parabole montante(coeff de x² positif). le point le plus bas peut se trouver absolument partout dans le plan, moitié au dessus du y=0 (pas de solution) moitié en dessous (solutions).
Pareil par la parabole descendante.
C'est une des réponses. Elle n'est pas la seule, mais sans doute la plus simple.
#6 - 19-10-2013 11:48:34
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
equations du second fegré
#7 - 19-10-2013 12:19:33
- Promath-
- Elite de Prise2Tete
- Enigmes résolues : 18
- Messages : 1416
- Lieu: Au fond de l'univers
equations du secobd degré
Oui, oui les réponses me sembles bien!
Mais...
Un promath- actif dans un forum actif
#8 - 19-10-2013 13:06:07
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
Equations du second degr
Maintenant, si on regarde les variables a,b,c de ax²+bx+c, il faut et il suffit que b²>=4ac pour avoir au moins une solution.
Question signe, si a et c sont de signes opposés, c'est toujours vrai, quel que soit le signe de b. Donc sur les 8 possibilités de signes (bac)=
+++= inconnu
++-=bon
+--=inconnu
+-+=bon
-++=inconnu
-+-=bon
---=inconnu
--+=bon
Donc la moitié au moins des variables admettent une solution.
Reste les cas des inconnues.
Il faut b²>4ac ou b>2rac(ac)
Ce qui laisse donc encore pas mal de solutions possibles. Et qui amène la question de la manière ce choisir dans R+ les nombres abc au hasard. C'est en précisant la loi de ce tirage qu'on peut répondre à la question !
#9 - 19-10-2013 13:34:54
- cogito
- Expert de Prise2Tete
- Enigmes résolues : 48
- Messages : 593
Eqautions du second degré
Bonjour 
Je pense qu'il y en a autant.
Imaginons le plan R2 coupé par l'axe des abscisses.
Prenons une parabole de la forme ax²+bx+c avec a > 0. Soit m son minimum.
L'axe des abscisses sépare le plan en deux demi plan :
P1={(x,y)|y>0}[/latex]et[latex]P2={(x,y)|y≤0}
L'équation ax²+bx+c est solvable ssi m∈P2 et l'équation n'est pas solvable ssi m∈P1.
Comme il y a autant de points dans P1 que dans P2 (même si P2 contient l'axe des abscisses en plus) alors il y a autant d'équations du second degré solvables que non solvables.
Note : pour a < 0 on a le même raisonnement avec les complémentaires de P1 et P2
Il y a sûrement plus simple.
#10 - 19-10-2013 16:05:42
- shadock
- Elite de Prise2Tete
- Enigmes résolues : 39
- Messages : 3334
rquations du second degré
Je pense que 2/3 des équations ont des solutions réelles.
En effet il y a trois cas de figure soit le discriminant des strictement supérieur 0 soit égal à 0 soit strictement inférieur...
Shadock 
"L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
#11 - 19-10-2013 18:12:49
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,039E+3
Equations du second dgré
C'est quoi ce "mais" ? 
Peux-tu préciser les "..." ?
#12 - 19-10-2013 19:22:06
- Promath-
- Elite de Prise2Tete
- Enigmes résolues : 18
- Messages : 1416
- Lieu: Au fond de l'univers
Eqautions du second degré
Il y a un mais car une fraction avec l'infini pourrait être faite?
Un promath- actif dans un forum actif
#13 - 19-10-2013 21:25:00
- gilles355
- Professionnel de Prise2Tete
- Enigmes résolues : 49
- Messages : 421
Equtions du second degré
Résoudre une équation du second degré revient à calculer le delta.
Si delta est strictement positif 2 solutions
si delta est strictement négatif 0 solution.
Jusqu'ici étant donné qu'il y a autant de réels strictement positifs que de réels strictement négatifs on pourrait dire qu'il y'en a autant sauf que :
si delta est égal à 0 il y a une solution.
Je dirais donc que ça fait pencher la balance sur le fait qu'il y a plus d'équations du second degré solvable que non solvable dans R.
#14 - 19-10-2013 21:49:56
- NickoGecko
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1822
Equations du secodn degré
Hello
Le déterminant d'une équation du second degré ax²+bx+c=0 est b²-4ac et la/les solution(s) sont réelles si b²-4ac >= 0
Si on trace dans l'espace les points tels que z²>4xy on obtient un "cone elliptique infini"
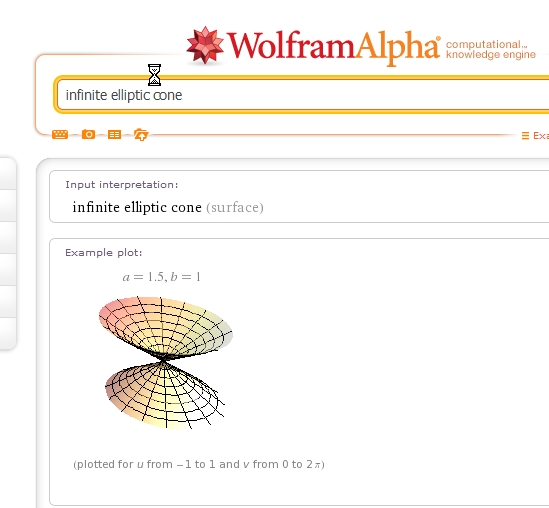
Cette infinitude me ferait dire qu'il y a "autant" d'équations à racine(s) réelles que complexes ...
A suivre ...
Bon WE

Il aurait pu pleuvoir, con comme il est ! (Coluche)
#15 - 19-10-2013 22:37:43
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,039E+3
Equations du second dgeré
Avec 2 "infinis" équivalents , oui, je pense... il y a autant de nombres entiers impairs que de nombres entiers pairs strictement positifs. Et pourtant on a un pair de plus : zéro.
Je sens que je vais adorer le moment de discussion qui va suivre ce fil. 
#16 - 20-10-2013 05:10:18
- dylasse
- Professionnel de Prise2Tete
- Enigmes résolues : 21
- Messages : 378
Equations du scond degré
On va prendre l'écriture réduite de l'équation : x²+2b+c=0
Le discriminant est D = b²-c
La question revient donc à se demander s'il y a plus de couple (b,c) tel que D est >=0 ou D<0.
Une représentation dans le plan nous permet de visualiser que les 2 zones correspondantes sont toutes les 2 infinies. Donc la réponse est que les 2 zones sont aussi grandes l'une que l'autre (c'est-à-dire qu'il existera une bijection de l'une vers l'autre).
Visuellement, il semble que D>=0 est plus grand que D<0 (on a plus qu'un demi-plan limité par la droite c=0), mais sur des ensembles infini ça ne veut rien dire.
Et même si une des zones était de surface finie, cela ne voudrait pas dire que une zone contient plus d'éléments que l'autre. Par exemple : est-ce qu'il y a plus de points tels que x²+y²<1 (disque de rayon 1) que de points tels que x²+y²>1 ?
Visuellement, on serait tenté de dire qu'il y en a plus à l'extérieur du cercle qu'à l'intérieur. Pourtant, il est facile d'associer à tout point du disque, repéré par (r,t) ces coordonnées polaires, son image (1/r,t). On s'aperçoit que c'est une bijection du disque vers l'extérieur du disque.
Enfin presque puisque le centre du disque n'a pas d'image : il y a un point de plus dans le disque qu'à l'extérieur 
#17 - 20-10-2013 10:45:53
- Promath-
- Elite de Prise2Tete
- Enigmes résolues : 18
- Messages : 1416
- Lieu: Au fond de l'univers
equations dy second degré
Masab: Ou sont les preuves?
Gilles: Moui mais de quoi dépend delta?
Les autres: Je pense aussi mais... Y a t il une démo concrète?
Un promath- actif dans un forum actif
#18 - 22-10-2013 13:46:50
- shadock
- Elite de Prise2Tete
- Enigmes résolues : 39
- Messages : 3334
equations su second degré
La démonstration concrète demande là à ton prof 
"L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
#19 - 22-10-2013 15:25:29
- Nombrilist
- Expert de Prise2Tete
- Enigmes résolues : 10
- Messages : 568
equations du secons degré
Question probabiliste: comment faîtes-vous pour faire un tirage aléatoire suivant une loi uniforme sur un domaine sans borne ?
#20 - 22-10-2013 16:17:21
- shadock
- Elite de Prise2Tete
- Enigmes résolues : 39
- Messages : 3334
Equatoins du second degré
On le fait sur un intervalle borné de R ça suffit non?
Par exemple sur [0,1]
PS : Je n'ai plus fais de proba depuis la terminale alors je ne suis pas sûr de ce que j'avance.
"L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
#21 - 22-10-2013 22:55:48
- MthS-MlndN
- Hors d'u-Sage
- Enigmes résolues : 49
- Messages : 12,414E+3
- Lieu: Rouen
Eqquations du second degré
Nombrilist a écrit:Question probabiliste: comment faîtes-vous pour faire un tirage aléatoire suivant une loi uniforme sur un domaine sans borne ?
Pour moi, c'est totalement impossible, vu que par définition, la loi uniforme est définie sur un intervalle de R.
Autre argument : par définition, la densité de probabilité vaut 0 partout si une des bornes du domaine est un infini. Donc ce n'est plus une densité de probabilité, vu que son intégrale sur R vaut 0...
Podcasts Modern Zeuhl : http://radio-r2r.fr/?p=298
#22 - 22-10-2013 23:52:45
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,039E+3
Equations du ssecond degré
J'ai envie de m'amuser...
Le discriminant est b^2-4ac.
ac est équiprobablement positif ou négatif (ou nul, on s'en fiche)
b^2 est toujours positif.
b^2-4ac est donc infiniment plus souvent positif ou nul que négatif. 
#23 - 23-10-2013 08:21:49
- MthS-MlndN
- Hors d'u-Sage
- Enigmes résolues : 49
- Messages : 12,414E+3
- Lieu: Rouen
Equations du second egré
Marrant : j'étais parti sur cette énigme en récupérant le même cône infini que NickoGecko, et j'en avais déduit qu'il y avait clairement moins d'équations du second degré insolubles dans R (à l'intérieur du cône) que de solubles dans R (à l'extérieur du cône). J'attends donc qu'on m'explique pourquoi l'intérieur et l'extérieur ont le même cardinal 
Podcasts Modern Zeuhl : http://radio-r2r.fr/?p=298
#24 - 23-10-2013 18:03:14
- kossi_tg
- Professionnel de Prise2Tete
- Enigmes résolues : 18
- Messages : 307
- Lieu: Montargis
equations du second defré
Proposition:
Soit l'équation: ax2+bx+c=0(1);
δ=b2−4ac
(1) est solvable dans R si δ≥0. Soit M(x,y,z) un point de l'espace, δ décrit l'ensemble des points de l'espace tel que z2≥4xy (2) soit un double cône symétrique par leur sommet commun (voir la photo de NickoGecko)
Je vais considérer un cube de l'espace et déterminer les fractions de volume de ce cube qui respectent (2) ou non.
Coté du cube: 2L (L un réel positif).
Ce cube sera centré à l'origine de l'espace donc x, y et z appartiennent à [-L;L]
Prenons le cas de l'égalité à partir de (2):
z2=4xy soit y=z24x (3) pour x non nul.
A partir de (3), on détermine rapidement les caractéristiques géométriques des cônes:
h=√22|z| (hauteur des cônes en fonction de z)
D=2|z| (diamètre de la base des cones en fonction de z)
α=109.47° (angle au sommet des cônes donné titre informatif)
Aux limites du cube considéré; |z|=L
Vcones=2π√23L3 (volume des 2 cônes)
Vcube=8L3 (volume du cube)
Tout point pris dans le cube mais à l'extérieur des 2 cônes respectent (2) donc la proportion des équations de 2nd degré solvables dans R est Vcube−VconesVcube=1−2π√224≈0.63 (cette proportion est indépendante de L)
Les équations de 2nd degré solvables dans R sont donc plus nombreuses que celles non solvables dans R.
Par ailleurs, un petit algorithme de tirage d'un milliard de triplets (a, b, c) m'a donné les proportions suivantes:
δ<0:37.2%
δ≥0:62.8%
Ce sont les résultats de cet algo qui m'ont d'ailleurs poussé à poster cette solution que je gardais dans mes brouillons:)
L’algorithme en question ici pour les curieux:
Spoiler : [Afficher le message] 
#25 - 23-10-2013 18:18:05
- shadock
- Elite de Prise2Tete
- Enigmes résolues : 39
- Messages : 3334
equations du secpnd degré
Bon bah ça va mon raisonnement n'était pas trop loin du résultat trouvé par kossi_tg 
"L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum







