 |
#1 - 03-12-2013 16:01:44
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3523
- Lieu: 94110
estimztion
Aujourd'hui, vous aurez droit à 2 énigmes pour le prix d'une  . .
1 : Une énigme mathématique dont je ne connais pas la réponse n'ayant jamais eu l'occasion de suivre un cours de probabilité au cours de mes études, mais qui me turlupine depuis quelques années déjà.
Un (grand) sac contient N pions (N inconnu) repérés par des nombres X (N << Xmax) (ou bien par des mots, des phrases, des images ou un mélange de tout cela) la seule condition étant qu'il n'y en ai pas deux identiques.
On tire un pion au hasard, on note sa référence dans une première liste, et on le remet dans le sac que l'on mélange bien à chaque fois. Si la référence est déjà présente dans cette liste, on l'inscrit dans une deuxième liste. Si elle existe déjà dans cette deuxième liste, on ne fait rien.
Au bout d'un certain temps , on a Tiré T pions différents (liste 1), et parmi ceux-ci P pions ont été tirés Plusieurs fois (liste 2).
Connaissant les valeurs T et P, comment en déduire une estimation de la valeur de N ?
Plus précisément, on recommence cette série de tirage un très grand nombre de fois en s’arrêtant à la valeur T donnée. On ne s'intéresse alors qu'aux tirages donnant la valeur P donnée. Qu'elle est alors la valeur moyenne de N ?
Application numérique : T = 1750 et P = 105.
2 : Une devinette. Pourquoi ce problème m'intéresse-t-il autant  ? ?
Plus précisément, que représentent pour moi les valeurs de T, P et N ?
Je laisse un certain temps :
- aux matheux pour me proposer une formule et une valeur de N afin que je puisse constater l'unicité ces réponses  ! Il va sans dire que la fin de cette période ne doit pas forcément clore les discutions. ! Il va sans dire que la fin de cette période ne doit pas forcément clore les discutions.
- aux autres pour résoudre la devinette.
Non... Spoiler : [Afficher le message] je ne cherche pas à estimer le montant de mon dernier casse en notant des numéros de billets de banque  . .
Non... Spoiler : [Afficher le message] je ne cherche pas à estimer le potentiel de clientèle de mon cabinet médical en notant des numéros de sécu  . .
D'ailleurs... Spoiler : [Afficher le message] ce n'est pas un nombre que je note... 
mais...Spoiler : [Afficher le message] une image  . .
#2 - 03-12-2013 19:47:34
- shadock
- Elite de Prise2Tete
- Enigmes résolues : 39
- Messages : 3334
Estimaiton
Pour résumé la situation parce que je suis analphabète  , ,
Par exemple dans mon sac il y a {1,2,3,4} il y a N=4 objets.
Et ces quatre objets, je le repère par {2,6,19,1000} puisque Xmax>>4 (je ne vois pour l'instant pas trop l’intérêt mais passons)
Donc si je tire au hasard 1 2 2 2 1 3 1 1 4 1 2
Je vais noter
Liste 1 : 2 6 19 1000
Liste 2 : 6 2
C'est bien ça ?
"L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
#3 - 03-12-2013 20:17:24
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3523
- Lieu: 94110
estumation
shadock a écrit :
Pour résumé la situation, par exemple dans mon sac il y a {1,2,3,4} il y a N = 4 objets.
Et ces quatre objets, je les repère par {2,6,19,1000} puisque Xmax>>4 (je ne vois pour l'instant pas trop l’intérêt mais passons)
Donc si je tire au hasard 1 2 2 2 1 3 1 1 4 1 2
Je vais noter :
Liste 1 : 2 6 19 1000
Liste 2 : 6 2
C'est presque ça  . .
En reprenant ton exemple, je dirai :
Par exemple dans mon sac il y a N = 4 objets repérés par {2,6,19,1000}
Donc si je tire au hasard 2 6 6 6 2 19 2 2 1000 2 6
Je vais noter :
Liste 1 : 2 6 19 1000
Liste 2 : 6 2
J'ajoute que l'on ne peut pas savoir par quoi sont repérés les objets avant de les avoir tiré au moins une fois. Et que si Xmax ~ N, on aurait déjà une bonne idée de la valeur de N, ce qui n'est absolument pas le cas. D'autre part, dans la réalité, T reste très inférieur à N, même si du point de vue mathématique, T peut devenir égal à N. Mais alors, le problème a perdu tout son intérêt  . .
#4 - 03-12-2013 22:31:40
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
estimztion
A mon avis, telle quelle, la question posée n'a pas grand sens.
#5 - 03-12-2013 23:33:05
- fix33
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1198
- Lieu: Devant un clavier depuis 1748
estimatipn
Oui, donc c'est N>>T qui importe, on se fiche de Xmax.
Tmoy et Pmoy sont fonctions de K, le nombre total de tirages et de N, le nombre de boules.
K=T+P+W, W étant les tirages de valeurs déjà apparues au moins 2 fois... Mouais...
Par ailleurs :
T = Tmoy(K,N) = (N^K-(N-1)^K) / N^(K-1)
Pas de démonstration pour le moment, déduction sur la base de quelques exemples...
P = Pmoy(K,N) = N^K - (N-1)^K - K*(N-1)^(K-1)
On voit que : T = [P + K*(N-1)^(K-1)] / N^(K-1)
Mouais...
Log T = Log(N^K-(N-1)^K) - (K-1)*Log(N)
Log P = Log [N^K - (N-1)^K - K*(N-1)^(K-1)]
Bof... 
A part me faire un immense tableur avec ces formules appliquées aux valeurs que tu proposes (en espérant qu'elles soient justes !), je ne sais pas si je peux avancer plus...
Je ne vien sur se site que pour faire croir que je suis treise intélligens.
#6 - 04-12-2013 11:04:13
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3523
- Lieu: 94110
estimatoon
fix33 en pleine recherche. Çà avance  . .
titoufred : on aurait pu présenter les choses plus simplement :
Un sac contient N objets tous différents (N inconnu, pour ne pas dire inconnaissable).
Après un certain nombre de tirages avec remise de l'objet dans le sac, on obtient T objets différents dont M ont été tirés plusieurs fois.
Peut-on en déduire une bonne approximation de N ?
#7 - 04-12-2013 11:34:13
- Nombrilist
- Expert de Prise2Tete
- Enigmes résolues : 10
- Messages : 568
estilation
Pour chaque objet Xi, on note leur probabilité d'être inscrits k fois après n tirages:
P(Xi=0)=(N−1N)nP(Xi=1)=C1n∗1N∗(N−1N)(n−1)P(Xi=2)=C2n∗1N2∗(N−1N)(n−2)+C3n∗1N3∗(N−1N)(n−3)
+...+Cnn∗1Nn∗(N−1N)(n−n)=1−P(Xi=1)−P(Xi=0)
Chaque variable aléatoire (Xi=2) suit donc une loi uniforme U(P(Xi=2)).
Donc, n variables aléatoires Xi indépendantes suivent une loi binomiale B(n,P(Xi=2)).
Si n est grand, alors n variables aléatoires Xi indépendantes suivent une loi normale N(nP(Xi=2),nP(Xi=0)P(Xi=1)P(Xi=2)) en posant N(m,σ).
Après, il faudrait réaliser l'encadrement à +−1.96σ et en déduire un encadrement de N. Je fais ça tous les jours de tête 
#8 - 04-12-2013 19:05:09
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
Etimation
Je vais légèrement corriger l'énoncé pour avoir une réponse plus en rapport avec ce qu'on attend.
Je ne conserve que la liste 1, c'est à dire le nombre d'objets différents obtenus une 1ère fois que je note m. L'important est la différence entre t et m.
Si 1 représente le lot complet des objets, et x l' échantillonage prélevé:
1ér tirage:
x donc il reste dans le tas non tiré 1-x.
2ème tirage:
x prélevé sur (1-x) donc il restera (1-x)-x(1-x)=(1-x)²
t ième tirage: il restera comme part non tirée: (1-x)^t.
La part y de la liste 1 est donc y= 1-(1-x)^t.
Si n objets: x=1/n et y=m/n
L'équation devient
m=n(1-(1-1/n)^t)
On connait t, on connait m, on peut retrouver n par dichotomie.
Pour obtenir un résultat significatif, il faut que t-m ne soit pas négligeable devant t. Plus il y aura un grand nombre de tirages, plus la différence sera significative, meilleure sera l'estimation. On peut déja avoir une bonne estimation à partir d'un (t-m)/t de 5%. Mais l'échantillonage restera assez important, de l'ordre de 10% de n.
#9 - 04-12-2013 22:35:41
- fmifmi
- Passionné de Prise2Tete
- Enigmes résolues : 18
- Messages : 87
estimayion
JE PENSE A DES BILLETS DE BANQUE
pour l’énigme mathématique je suis dessus mais j'ai du mal
#10 - 04-12-2013 22:53:30
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3523
- Lieu: 94110
estumation
Çà y est, les "matheux" se sont lancés dans de savants calculs ... qui ne débouchent pas forcément sur les mêmes formules, formules qui, pour certaines, nécessiteraient la puissance d'un supercalculateur  ! !
Je leur laisserai dans 2 jours tout le loisir de comparer entre eux ces réflexions qui dépassent mes propres capacités de concentration  . .
Mais je commence à me demander si j'obtiendrai la réponse au problème concret qui m'intéresse, avec les valeurs numériques indiquées pour T et P, valeurs qui, dans un mois ou dans un an auront eu le temps d'évoluer.
Non fmifmi, je n'ai pas réalisé de casse, et il ne s'agit pas de piocher des billets de banque dans un grand sac pour éviter d'avoir à les compter  ! !
J'attends toujours des propositions de la part des autres en ce qui concerne la réalité de ce problème, problème auquel je suis sans doute le seul à m'intéresser, mais qui, pour ceux qui suivent un peu les énigmes que je pose, devrait paraître évident  . .
#11 - 05-12-2013 00:16:35
- Nombrilist
- Expert de Prise2Tete
- Enigmes résolues : 10
- Messages : 568
esrimation
C'est un problème qui ressemble quand même pas mal à celui que j'ai posté il y a quelques temps:
http://www.prise2tete.fr/forum/viewtopic.php?id=11147
Je m'interrogeais sur la vérification que le tirage du loto soit réellement aléatoire (i.e. chaque boule suit une loi uniforme sur un grand nombre de tirage, ce qui a amené rapidement à une estimation de l'ensemble des tirages par une loi normale).
Le problème de la sortie des boules du loto sur un grand nombre de tirage est analogue au problème que tu poses. Dans ce problème, on disposait alors de toutes les informations sur le tirage. Malgré tout, on voit que l'intervalle de confiance à 95% est énorme: on peut considérer le tirage comme aléatoire si les boules sont tirées entre 59 et 92 fois, avec tout de même 3700 boules tirées ! Sacré écart. Dans ton cas, il n'y a qu'environ 2000 tirages et il nous manque l'information sur le nombre de sortie de chaque élément. Donc, en toute logique, l'écart-type de l'estimateur doit être encore plus grand. Je ne suis pas certain que l'on puisse estimer N avec les indices dont on dispose. Mais peut-être que d'autres ont trouvé ?
Et pour la devinette: es-tu un collectionneur ? Un numismate, par exemple ?
#12 - 05-12-2013 10:36:18
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3523
- Lieu: 94110
estimarion
nodgim : je conçois qu'élever un nombre à la puissance 1750 puisse poser quelques problèmes... Mais si on passait par les logarithmes ?
Nombrilist : - indépendamment de la valeur de l'écart-type, on doit pouvoir trouver une valeur moyenne, même très approximative, non ?
- on peut dire si on veut que je suis un "collectionneur"... mais pas d'objets matériels. Je ne suis donc pas numismate.
#13 - 05-12-2013 11:48:42
- dylasse
- Professionnel de Prise2Tete
- Enigmes résolues : 21
- Messages : 378
Estmation
Appelons T(z) et P(z) la longueur des listes des pions tirés au moins une fois et de ceux tirés 2 fois ou plus, après z tirages.
Pour le tirage suivant, nous avons 3 cas :
Cas 1 : On tire un pion jamais tiré, cette situation se produit dans N - T(z) cas sur les N possibles, soit une probabilité de (n-T(z))/N. Dans ce cas, T(z+1)=T(z)+1 et P(z+1)=P(z).
Cas 2 : on tire un pion tiré précédemment 1 seule fois : proba : (T(z)-P(z))/N, T(z+1)=T(z) et P(z+1)=P(z)+1.
Cas 3 : on tire un pion déjà tiré 2 fois ou plus : proba : P(z)/N, T(z+1)=T(z) et P(z+1)=P(z).
On en déduit T(z+1) = (N-T(z))/N (T(z)+1) + (T(z)-P(z))/N T(z) + P(z)/N T(z)
soit : T(z+1) = T(z) (1-1/N) + 1
Cette suite définie par récurrence s'exprime en fonction de z (après un décalage U(z) = T(z) - N) : T(z) = N (1 - (1-1/N)^z)
Pour P, la formule de récurrence est : P(z+1) = P(z) + T(z)/N - P(z)/N.
L'expression de P(z) en fonction de N et z est définie et unique mais dépasse mes possibilités...
On peut néanmoins construire nos 2 suites avec excell et tâtonner pour résoudre l'application numérique avec T=1750 et P=105.
On trouve la valeur la plus probable de N = 15180 et les 2 valeurs de T et P après z=1860 tirages (ce qui signifie en passant que 5(=1860-1750-105) tirages ont sorti un pion pour la troisième fois ou plus).
#14 - 05-12-2013 16:22:12
- masab
- Expert de Prise2Tete
- Enigmes résolues : 44
- Messages : 971
Estimatin
Prenant le train en marche, je me contenterai de l'application numérique.
Application numérique : T = 1750 et P = 105
Une simulation permet de montrer que N se situe autour de 15160.
#15 - 05-12-2013 18:13:29
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3523
- Lieu: 94110
Estimtaion
Merci à dylasse et masab qui aboutissent approximativement au même résultat pour l'application numérique  . .
#16 - 05-12-2013 23:50:19
- fix33
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1198
- Lieu: Devant un clavier depuis 1748
Estimaton
Pour la 2nde question, voici les idées qui me viennent : recherche de faux-positifs, recherche génétique, recherche statistique autour des jeux d'argent... Bof !
Je ne vien sur se site que pour faire croir que je suis treise intélligens.
#17 - 06-12-2013 09:42:13
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3523
- Lieu: 94110
stimation
Non, rien de tout cela fix33.
Mais je signale à tous que j'ai éliminé pas mal de pistes dans le sujet  . .
#18 - 06-12-2013 11:10:57
- masab
- Expert de Prise2Tete
- Enigmes résolues : 44
- Messages : 971
Estimatiion
Une devinette
Peut-être ce problème a un lien avec le TRAPEZOMINO...
En vue d'estimer à rotation près le nombre de grilles de Trapézomino...
Commentaire suite au message suivant de Jack : en fait ce ne sont pas les lettres de Trapézomino qui m'ont guidé (j'ai mis en gras T, P, N pour agémenter ma réponse) ; c'est le lien entre Jack et le Trapézomino qui m'a fait imaginer cette réponse ; j'ai hésité plusieurs jours avant de la soumettre !
#19 - 06-12-2013 15:31:32
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3523
- Lieu: 94110
#20 - 06-12-2013 15:37:12
- enigmatus
- Expert de Prise2Tete
- Enigmes résolues : 0
- Messages : 561
Estimtion
Bonjour,
Je n'ai pas de réponse à la question telle qu'elle est posée, mais j'ai fait quelques essais.
Un essai consiste, pour N fixé, à effectuer des tirages jusqu'à ce que T=1750, et à relever P à ce moment-là
En faisant 10000 essais par valeur de N, j'obtiens des valeurs de P très dispersées, et j'en calcule la moyenne (l'écart-type est de l'ordre de 10).
Voici le tracé de la moyenne de P en fonction de N :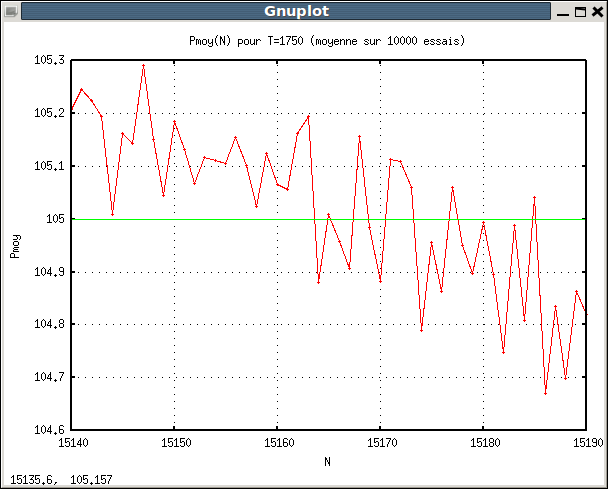
Pour N aux alentours de 15170, la moyenne de P est voisine de 105. J'ignore si on peut en déduire quelque chose dans l'autre sens.
#21 - 06-12-2013 16:07:52
- Nombrilist
- Expert de Prise2Tete
- Enigmes résolues : 10
- Messages : 568
estimayion
Tu complètes ta collection de vignettes Panini et tu en mets une série de côté pour ton gosse ?
#22 - 06-12-2013 18:15:52
- Neotenien
- Passionné de Prise2Tete
- Enigmes résolues : 43
- Messages : 56
Etimation
Bonjour
Si je comprend bien, dans la liste 2, chaque élément n'appaarait aussi qu'une seule fois ?
Du coup, on a un une probabiité dont on cherche la cardinalité Omega de la population (qu'on ne connait pas) et sur laquelle on effectue un tirage avec remise.
Eh bien à première vue, je dirais que ta liste 2 ne sert à rien, on a plutôt affaire à un problème de limites en analyse. Il faut effectuer un nombre de tirage proche de l'infini et déterminer plutôt à partir de quel moment on considère qu'on est proche de N suivant un nombre de tirages successifs d'éléments déjà tirés.
Il faudrait compter le nombre des tirages de chaque élément, faire leur somme et si cette somme >= à la moitié du carré du nombre d'éléments de la liste 1 (la surface d'un triangle) peut-être que tu peux te dire que tu es proche du nombre N ? Mais ceci est plutôt empirique...
Je pense qu'il n'y a pas, à ma connaissance, de moyen pour avoir ta réponse, uniquement avec les éléments que tu as doinné. Il faut absolument compter le nombre de chaque élément tiré.
#23 - 06-12-2013 19:24:22
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3523
- Lieu: 94110
#24 - 06-12-2013 19:33:15
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,043E+3
estimatiin
Aucune idée pour la question 1 
Pour la deux, tu cherches à déterminer le nombre de solutions à ton jeu de trapézomino ?
#25 - 06-12-2013 20:51:02
- elpafio
- Elite de Prise2Tete
- Enigmes résolues : 43
- Messages : 1017
Estmation
Bonsoir Jackv,
L'objectif serait-il d'essayer d'estimer le nombre de solutions du Trapézomino, en tenant compte de la subtile pièce joker qui peut remplacer une autre pièce ?
Dans la deuxième liste serait placée toute solution similaire à l'une de celles de la première liste, mais s'en différenciant par le fait que la pièce joker y remplacerait une des pièces classiques.
J'ai l'impression que cette idée n'est pas clairement exposée...
Et c'est encore moins clair dans ma tête 
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum







