Question ultime

42

Merci pour cette énigme. Si j'ai bien compris:

- Il faut partir d'une extrémité du damier et parvenir exactement à celle d'en face ?
- On ne peut avancer que d'une case à la fois (autrement dit, si il n'y a pas de point présent en diagonale ou tout droit, on a perdu) ?
- La portion de chemin entreprise entre deux points consécutifs doit toujours rapprocher de l'extrémité à atteindre ?

Comment choisit-on l'emplacement de départ ? Je suppose qu'on le choisit après placement des points ? Peut-on démarrer à partir d'un emplacement où on n'a pas mis de point ?

Qu'est-ce que c'est, le "bout" d'une grille ?

Doit-on comprendre qu'il faut aller du coin en bas à gauche vers le coin en haut à droite sans jamais redescendre ni retourner vers la gauche ?

Pour qu'il y ait calcul de probabilité, il faut bien qu'il y ait un tirage aléatoire à un moment donné. Quel est ce tirage aléatoire ? A mon avis, c'est l'emplacement de départ, mais j'aimerais être sur.

Je ne comprends vraiment rien à ton problème.  C'est quoi ces trucs de gauche droite haut bad ? 

@gwen : Le dessin ne peut être plus explicite le but est d'aller d'un segment voilà ce sera peut-être plus clair comme ça, d'un segment de la grille au segment opposé le plus loin ^^ je sais je ne comprends pas pourquoi vous ne comprenez pas je crois que je vais finir par faire une vidéo pour vous expliquer mon énigme, une première dans l'histoire de P2T
Si la grille est carrée, tu pars d'un bord du carré, tu te mets sur le point que tu veux après avoir fait ton tirage aléatoire par exemple dans le cas d'une grille (3,3) il y a au total 9 points au max que tu peux placer sur la grille, si tu décides de tirer aléatoirement 5 points sur la grille tu regardes si tu as au moins un point sur le bord inférieur du carré que forme la grille tu regardes si tu as au moins un point sur le bord du haut du carré et que tu as un chemin entre deux de ces points alors tu pourras traverser d'un bout à l'autre...

@Fix où tu as vu dans l'énigme que le but était de bloquer les chemins? On considère tous les chemins possibles Sur la grille (3,3) si tu places 3 points aux intersections des lignes du bas et du milieu alors il te reste plus qu'un point à placer sur la ligne du haut pour être sûr à 100% de pouvoir traverser d'un bout à l'autre donc [latex]\alpha_{(3)}^1=7[/latex] voilà c'est tout

Euh, mais :
- il s'agit du nombre de points minimum pour pouvoir tracer un chemin ("horizontal" et "vertical") ou ("horizontal" ou "vertical") ? Dans ton énoncé, je comprends la 2nde possibilité. Et à partir du moment où j'aurais tous les points sur la ligne du bas ou celle du milieu, dans ton exemple, je n'ai pas besoin de chercher d'autres points puisque j'ai plusieurs chemins horizontaux...
- Est-ce qu'un chemin "vertical" peut passer par des points latéraux (bords gauches ou droites) ? Je suis parti du principe que c'était possible...

Mon raisonnement dans mon post précédent visait juste à calculer le nombre minimal de points qu'il suffit de confisquer au joueur pour empêcher tout chemin vertical et horizontal. A partir de là, on en déduit le nombre minimal qu'il suffit d'avoir pour tracer ces fameux chemins !

Les points sont tirés chacun de manière équiprobable.

Et je ne vois pas pas pourquoi vous désespérez tous avec ces histoires de chemin, il suffit de prendre la définition au pied de la lettre...

Admettons notre grille est formée par un carré ABCD le but est d'aller de [AB] vers [CD] vous tracer votre grille à l'intérieur du carré et bien évidemment les bords du carré en font parti...si le dessin n'est pas clair avec ça je peux plus rien pour vous moi et ensuite vous tracez vos chemins en reliant les points de proche en proche dans toutes les directions !

Sydre oui c'est exactement ça

Bonjour,

pour le cas où la probabilité est 1 je ne suis pas d'accord avec la formule de Sydre.
Je dirais plutôt :
[TeX]\alpha^1_{(m,n)}=\max(m(n-1),n(m-1))+1[/TeX]
Enfin si j'ai bien compris l'énoncé

Voilà comment j'ai compris l'énoncé.

On a une grille comme ci-dessous (ici 4x4) :



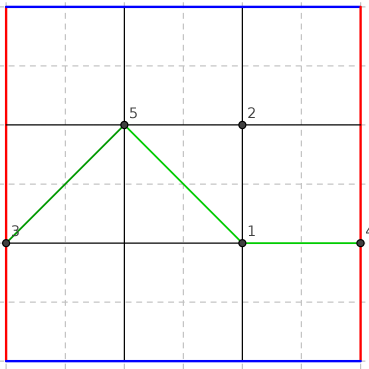
On tire aléatoirement des points parmi les intersections.
Ici on a eu un tirage de cinq points qui sont numérotés dans l'ordre dans lequel ils ont été tirés. Ils se trouvent que ces 5 points (en fait seulement quatre d'entre eux même) forment un chemin car je peux en reliant les points, relier les deux côtés rouges (un exemple de chemin est tracé en vert sur le dessin). Dans l'exemple cité ici, il n'existait pas de chemin avant le tirage du cinquième point.
Si j'avais pu relié les deux côtés bleus, j'aurais eu également un chemin.

J'interprète [latex]\alpha^1_{(m,n)}[/latex] comme étant le plus petit nombre de points qu'il faut tiré dans une grille m x n pour être sûre d'avoir un chemin, c'est-à-dire pour être sur de pouvoir reliés soit les deux côtés bleus, soit les deux côtés rouges en reliant les points comme indiquer dans l'énoncer.

Maintenant, je ne sais pas si cette interprétation est la bonne ou pas.

EDIT : Du coup, je rectifie, je suis effectivement d'accord avec la formule de Sydre .
Pardon.

Mais dans ce cas on aurait [latex]\alpha^1_{4}=10[/latex] et [latex]\alpha^1_{3}=5[/latex] qui sont différents des nombres données par shadock, donc je ne sais pas si c'est la bonne interprétation .

fix33 a écrit:

Je suis peut-être non-comprenant, mais avec des réponses à mes questions, j'aurais pu changer !

Mais pourquoi veux-tu changer ?
Tu as la même réponse que Sydre et Shadock a dit à Sydre qu'il avait bon !

Gwen27 a écrit:

Si c'est ça, je ne comprends toujours pas les exemples donnés en dessin... hmm

Ben moi, je ne vois pas d'exemple de dessin donné par Shadock...

Je ne comprends rien à ce sujet....

Bah vous dites que alpha exposant 1 et indice 3 = 5 (désolé je maîtrise pas le latex).

Bah vous prenez la grille on met 5 points, un au centre, et un à chaque coin et voilà on peut passer à coup sûr de haut en bas et il y a 5 points. Sur la figure, il y'en a plus mais on demande le minimum. Je suis bon ?