 |
#26 - 17-06-2014 14:52:39
- halloduda
- Professionnel de Prise2Tete
- Enigmes résolues : 24
- Messages : 495
- Lieu: Ardèche
des bananes et un chamezu (2)
J'ai considéré que le chameau pouvait porter 1000 bananes
y compris celle qu'il était en train de manger.
Si cette dernière est en plus, ça fait effectivement un peu moins de bananes au départ car il peut partir avec 1000 bananes au lieu de 999.
De mémoire, la première étape faisait alors environ 48 km.
D'où la conso chameau environ 35 à 38 de moins. Le 48 était arrondi.
7635 à 7640 bananes à peu près.
J'ai fait le calcul mais je n'en ai plus les détails.
Si je les retrouve, je les publierai.
#27 - 17-06-2014 14:54:29
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
Ds bananes et un chameau (2)
Je me suis trompé sur le nombre de tas, les 1000 dernières bananes ne sont plus à transporter, mais sinon mon nombre me semble correct... A moins qu'il faille compter en tas d'un nombre de bananes entier !
Auquel cas on aurait comme distances :
Départ : 8000 bananes
Il faudrait parcourir 1000/(2*8-1)=66,667 qui devient soit :
1) On arrondit les distances aux 500m inférieurs :
2) On arrondi aux 500m supérieur, et on garde le plus avantageux des 2, ce qui donne ici :
66.5 km et on dépose 7x(1000-66.5)+(1000-66.5)=7002.5 bananes dont 2.5 seront perdues.
77 km et on dépose 5999 bananes
91 km et on dépose 4998 bananes
111 km et on dépose 3999 bananes
143 km et on dépose 2998 bananes
200 km et on dépose 1998 bananes
Reste à parcourir 1000-(66.5+77+91+111+143+200)=313 km et on peut déposer 1064 bananes.
Il suffit de ne pas les prendre au départ et on se retrouve donc à emmener 8000-64=7936 bananes
Pour la variante avec retour, je cherche encore...
#28 - 17-06-2014 15:28:03
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
Des bananes et un chaameau (2)
Pour le retour, je pense que comme plus la distance est grande, plus la banane coûte cher, alors le mieux est sans doute de déposer une banane à chaque kilomètre en prévision du retour...
Au lieu d'avoir un nombre impair de trajets pour emmener un multiple impair de 1000 bananes d'un tas vers le suivant (des aller-retour +1 dernier aller simple), il faut ajouter une banane du km, ce qui équivaut à un retour supplémentaire. On obtient donc des nombres pairs de trajets.
En partant de la fin : 2000-3d1-d1=1000 (les 2000 du tas moins 2 allers et un retour moins une banane du km pour arriver à 1000 au marché)
On trouve d1=250 km
3000-5d2-d2=2000
d2 = 166.5 km ; dTotale=250+166.5=416.5 km
d3 = 125 km ; dT=541.5 km
d4 = 100 km ; dT=641.5 km
d5 = 83 km ; dT=744.5 km
d6 = 71.5 km ; dT=816 km
d7 = 62.5 km ; dT=878.5 km
d8 = 55.5 km ; dT=934 km
d9 = 50 km ; dT=984 km
d10 = 45.5 km ; dT=1029.5 km
Il faudra donc 9 tas intermédiaires d'où près de 11 000 bananes ! (je trouve 10976 exactement)
J'espère être proche de la solution...
#29 - 17-06-2014 20:54:05
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
Des bananse et un chameau (2)
@halloduda : c'est bien 1000 bananes en tout, y compris celle qu'il mange pour le premier kilomètre. Je te disais juste que ce n'est pas la peine de la distinguer des autres.
@golgot59 : Non, on ne s'oblige pas à parcourir des nombres de kilomètres entiers ou à faire des tas de bananes en nombres entiers. On peut faire bien moins que ce que tu proposes.
#30 - 17-06-2014 21:31:59
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 5,997E+3
dzs bananes et un chameau (2)
Si, on y arrive en faisant des tas de bananes entiers.
#31 - 17-06-2014 22:14:04
- halloduda
- Professionnel de Prise2Tete
- Enigmes résolues : 24
- Messages : 495
- Lieu: Ardèche
des bananes et un chamezu (2)
Titoufred a dit :
@golgot59 : Non, on ne s'oblige pas à parcourir des nombres de kilomètres entiers ou à faire des tas de bananes en nombres entiers.
Ceci explique nos différences.
D'accord pour les nombres de kilomètres non entiers, sinon c'est pénalisant.
Pour ne pas exagérer, j'arrondis au mètre près, ça me coûte une banane.
1 Quand je charge le chameau je lui mettais des bananes entières,
d'où le 999 car de ce fait il en a toujours une entamée en cours.
2 Je ne déposais des tas que de bananes entières,
puisqu'elles sont destinées à la vente.
Pour les deux je faisais une erreur car les morceaux de banane peuvent servir
à nourrir le chameau et on peut partir avec 1000 en tout.
Il faut quand même arriver avec 1000 bananes entières pour les vendre.
Donc viser 1001 à l'arrivée ? (à vérifier)
Il suffit de calculer la position x du premier dépôt, cela permet de calculer la consommation du chameau=15x+6000
et de partir avec 15x+7000 arrondi par excès plus 1 pour les entières.
Nota : x est de l'ordre de 45 km.
#32 - 17-06-2014 22:49:32
- elpacha
- Amateur de Prise2Tete
- Enigmes résolues : 0
- Messages : 2
Des bananes et un chaameau (2)
bonsoir il doit acheter 5750 bananas:lol:
#33 - 17-06-2014 23:45:32
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
De sbananes et un chameau (2)
@halloduda : gwen me signale qu'on n'a pas besoin de couper les bananes en morceaux, et il a tout à fait raison. D'ailleurs, comme tu le dis, elles seraient invendables ! Donc je résume : on s'autorise à faire des trajets n'ayant pas un nombre entier de kilomètres mais on ne s'autorise pas à couper les bananes en petits morceaux.
@elpacha : non, ce n'est pas ça 
#34 - 18-06-2014 00:55:18
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
Des bananes et u chameau (2)
Bon, j'ai trouvé mieux en remontant le temps :
Avec 1000 bananes à l'arrivée, on a besoin de 2000 bananes à 333.333 km (1000/3) de l'arrivée, de 3000 à 533.333 km (1000/3+1000/5), etc jusqu'à 7000 bananes à 955.13 km (1000/3+1000/5+...+1000/13).
Il reste donc 44.866 km à parcourir 15 fois, ce qui nécessite 7673 bananes en tout !
Bon, j'espère que ce coup-ci c'est bon !
Pour le retour, mon idée de base n'est pas la bonne ou est-elle juste mal utilisée ? (placer 1 banane à chaque km en prévision du retour)
PS : Désolé de polluer autant ton topic 
#35 - 18-06-2014 09:13:06
- halloduda
- Professionnel de Prise2Tete
- Enigmes résolues : 24
- Messages : 495
- Lieu: Ardèche
Des bananees et un chameau (2)
@halloduda :
gwen me signale qu'on n'a pas besoin de couper les bananes en morceaux, et il a tout à fait raison. D'ailleurs, comme tu le dis, elles seraient invendables ! Donc je résume : on s'autorise à faire des trajets n'ayant pas un nombre entier de kilomètres mais on ne s'autorise pas à couper les bananes en petits morceaux.
Cela confirme donc mon calcul avec 999 sauf pour le tout premier départ à 1000.
Les escales sont aux distances (arrondies au décamètre)
45.84 122.68 213.49 324.49 467.20 667
ce qui fait une livraison de 1001 bananes dont une non entière
et uns consommation chameau de 688+6x999=6682 bananes
Il faut donc partir avec 7783 bananes.
Avec retour, les escales sont aux distances :
36.25 86.20 141.70 204.13 275.48 358.73 458.63 583.50 750
Là, on peut livrer 1000 bananes toutes entières en effectuant la dermière escale avec 1000, livraison 500+500.
La conso chameau est 9717, il faut partir avec 10717 bananes.
EDIT
On ne voit pas pourquoi on ne pourrait pas laisser des bananes coupées
dans les escales, utilisables pour le retour car non à vendre.
Alors on doit pouvoir faire un peu mieux.
#36 - 18-06-2014 11:39:04
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 5,997E+3
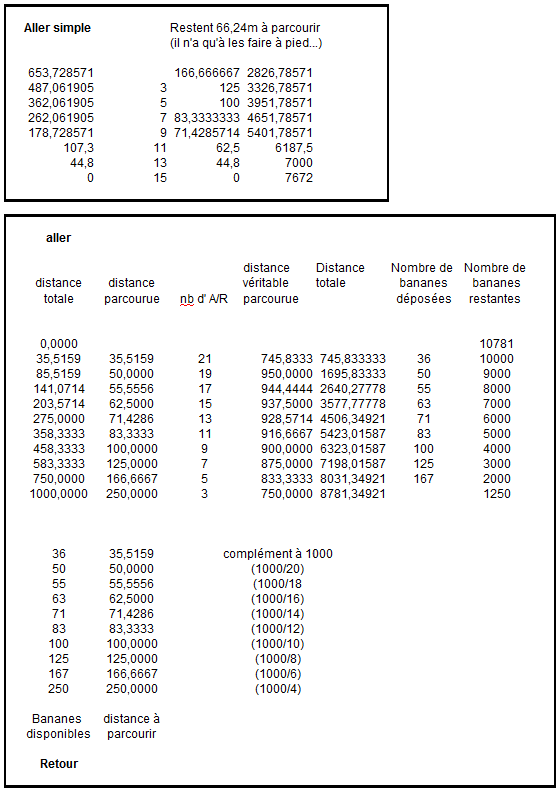
Des bananes et un chameau (2))
Avec le détail :
#37 - 18-06-2014 14:24:32
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
des bznanes et un chameau (2)
@golgot59 : Oui, bravo ! Pour le retour, ton idée de base est bonne oui.
@halloduda : Tu n'es plus très loin. Tu n'as pas besoin de livrer 1001 bananes. Autant utiliser la 1001ème pour autre chose. Je ne sais pas pourquoi tu t'évertues à distinguer la première banane consommée de toutes les autres qui le sont. Pour le retour, c'est l'idée mais tu dois faire une erreur de calcul quelque part.
@gwen : Je n'ai pas bien compris le 1er tableau (il n'y a pas les titres des colonnes) et j'ai l'impression que tu ne trouves pas les mêmes distances que moi, bizarre. Pour le deuxième tableau et le problème du retour, on trouve pareil.
#38 - 18-06-2014 15:10:24
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
fes bananes et un chameau (2)
Merci !
Alors je m'y recolle pour le retour :
Avec 1000 bananes à l'arrivée, on a besoin de 2000 bananes à 250 km (1000/4) de l'arrivée, de 3000 à 416.7 km (1000/4+1000/6), etc jusqu'à 10000 bananes à 964.48 km (1000/4+1000/6+...+1000/20).
Il reste donc 35.516 km "à parcourir" 22 fois (en fait 21 fois plus la banane à déposer à chaque km), ce qui nécessite 10781.3 donc 10782 bananes en tout !
Je ne suis pas sûr que ce soit cela car ce n'est pas beaucoup mieux que ma réponse précédente...
#39 - 18-06-2014 15:19:12
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 5,997E+3
Dees bananes et un chameau (2)
Le premier est bêtement recopié.
Le truc est de partir de la fin. Avec des trajets à 1000 bananes, il en faut 2000 avant et on fera 3 fois le trajet.
Donc 333,333333 km ...
On en avait donc 3000 avant sur 5 trajets : 200 km
....
De fil en aiguille, on voit que 7000 ne suffisent pas
(elles ne nous font faire que 955 km )
Et on ajuste :
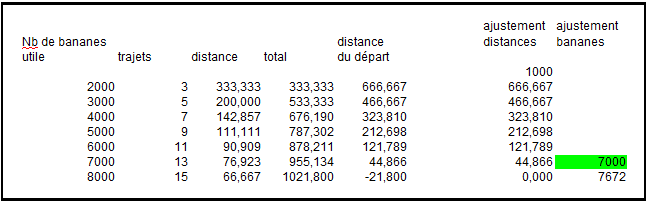
Idem pour le trajet avec retour sauf qu'on compte 4 fois chaque distance car il faut laisser un tas de banane permettant de la couvrir au retour.
#40 - 18-06-2014 16:07:08
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
Des bananes et un chammeau (2)
@golgot59 : Oui, bravo pour le retour !
@gwen : ok, je comprends mieux maintenant.
#41 - 19-06-2014 14:36:28
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
Ds bananes et un chameau (2)
Vous pouvez à présent voir les réponses de gwen27, nodgim, golgot59 pour le problème de l'aller ; de gwen27 et golgot59 pour le problème de l'aller-retour. Bravo encore à eux !
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum








